Oct
24
¡La Naturaleza! Además de Bella, es… ¡Asombrosa!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Simetrías ~
Clasificado en Simetrías ~
 Comments (0)
Comments (0)
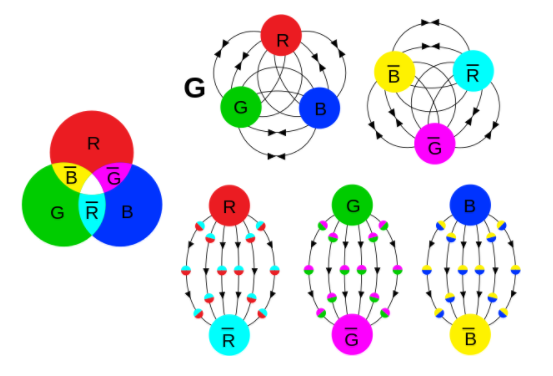
No pocas veces nos encontramos con hechos que aunque han tenido la participación de los humanos, parecen tener su origen en otro ámbito más alto de éste nuestro, en otro lugar donde el entendimiento sería superior y las mentes tuvieran la potestad de ver secretos de la Naturaleza profundamente escondidos. En física tenemos multitud de ejemplos de esto que digo: Me vienen a la mente las ecuaciones conocidas como de Yang-Mills que indicaban que los gluones, las partículas gauge que transportan la fuerza más poderosa de las cuatro conocidas para mantener unidos los Quarks dentro del núcleo, debían carecer de masa, como los fotones y los gravitones.
¿Por qué, entonces la fuerza nuclear fuerte se hace sentir sólo a corta distancia, cuando la luz y la gravitación tienen un alcanza infinito?

La respuesta la tenemos en la Cromodinámica cuántica, la teoría de la fuerza intensa, es que ésta aumenta su poder cuando los Quarks que aprisiona tratan de separarse, en vez de debilitarse como el electromagnetismo y la gravitación con la distancia, la fuerza nuclear fuerte aumenta. Ahí surgió el origen de confinamiento de los Quarks” que, obligados por una “nube” de Gluones, el Bosón mediador de esta fuerza.

También aclaró la Cromodinámica cuántica el funcionamiento de la fuerza débil: el fenómeno antes misterioso de la desintegración radiactiva Beta que pudo ser interpreta ahora como la conversión de un Quark down en un Quark up, convirtiéndose el neutrón, formado por dos Quarks down y un Quark up, en un protón que consiste en dos Quarks up y un Quark down.
La simetría como se pudo ver más tarde, iba a desempeñar un papel destacado en el ulterior desarrollo de la teoría cuántica de campo, y hasta señaló el camino hacia una teoría unificada de la “supersimetría”, capaz de unir todas las partículas y campos bajo el manto de un sólo conjunto de ecuaciones. Yang escribió:


Simetría especular
“La Naturaleza parece aprovechar la representación matemática simple de las leyes de simetría. La elegancia intrínseca y la bella perfección del razonamiento matemático involucrado, así como la complejidad y profundidad de sus consecuencias físicas, son una gran fuente de estímulo para los físicos. Uno aprende a alentar la esperanza de que la Naturaleza posee un orden que podemos aspirar a comprender.”



La Simetría de la Naturaleza nos rodea por todas partes y, a nuestro alrededor, miremos donde podamos mirar, allí está presente y, sin embargo, de ninguna manera son manifiestas todas las simetrías de la Naturaleza. Vivimos en un mundo imperfecto, en el que muchas de las simetrías que aparecen en las ecuaciones están rotas.

La violación de la paridad inducida por campos…

“TD Lee fue un físico teórico único en su generación, cuyo extraordinario trabajo y mentoría de jóvenes científicos ha tenido un impacto duradero”, dijo la directora del Laboratorio Brookhaven, JoAnne Hewett, quien también es física teórica. “La formulación teórica de Lee y Yang sobre la violación de la paridad (que luego fue demostrada experimentalmente por Chien-Shiung [CS] Wu) fue innovadora y es la base de las interacciones débiles y del actual Modelo Estándar de física de partículas. Trabajé en paneles con TD y siempre me asombró su presencia”.
De todos es bien conocido que, el mismo Yang, en colaboración con Tsung Dao Lee, identificó una discreta simetría en la fuerza débil, llamada violación de la paridad. En 1956, ambos predijeron sobre bases teóricas, que el espín de las partículas provenientes de la desintegración Beta mostrarían una ligera preferencia por una dirección sobre la otra. Experimentos realizados, así lo confirmaron y les valió el Premio Nobel a Lee y Yang (aunque no a Wu por razones desconocidas). Aquello sirvió para atraer la atención sobre el hecho de que la Naturaleza, sea simétrica en algunos aspectos y asimétrica en otros.

Las conocidas como moléculas quirales pueden existir en dos formas, siendo una la imagen especular no superponible de una sobre la otra, incluso aunque ambas tienen la misma composición química … Si bien los experimentos de laboratorio tienden a producir cantidades iguales de las versiones dextrógiras y levógiras, muchas de las moléculas quirales encontradas en organismos vivos proceden de una de las variedades … Por ejemplo, los aminoácidos que forman las proteínas solo aparecen en la forma levógira, mientras que los azúcares del ADN sólo en la dextrógira … ( la dextrosa o glucosa, es un azúcar que desvía el plano de polarización a la derecha) …

Los científicos han debatido desde hace mucho sobre esta asimetría en los seres vivos … Algunos han defendido que un número igual de ambas versiones de la molécula quiral estaba presente en el inicio de la vida, y que sólo durante la evolución biológica tuvo lugar el desequilibrio … Esa visión se ha ido haciendo cada vez menos popular, no obstante, al darnos cuenta de que el proceso fundamentalmente importante del plegamiento de proteínas parece requerir un desequilibrio quiral, aunque el que la naturaleza haya seleccionado la quiralidad derecha o izquierda para cada molécula durante la evolución implicaría procesos extremadamente complejos …





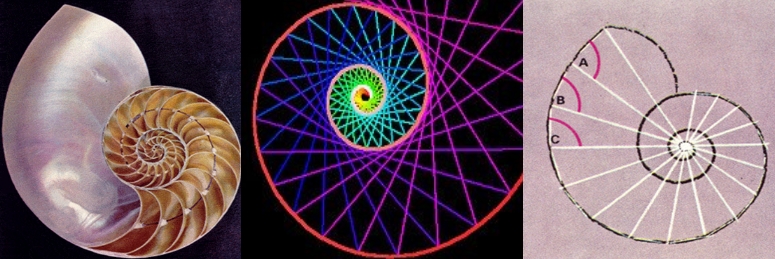
Los cuernos de una cabra paquistaní, la imagen de un ciclón visto desde el espacio, una galaxia o una concha, la chica que arriba nos mira. Son formas que se nos viene a la vista, aspectos de la realidad que llaman poderosamente nuestra atención y nos lleva a preguntar: ¿Por qué se forman y repiten esas figuras una y otra vez, y, en cada caso, una es la “copia exacta” de todas las demás de su género? ¿Es posible que el hombre, al contemplar tales maravillas comenzara a hacer preguntas y diera lugar al nacimiento de la Ciencia? Las matemáticas comenzaron por el asombro que despertaban las formas geométricas y de la misma manera, nacieron los primeros problemas de la física clásica centrada en las órbitas de los astros y las trayectorias de proyectiles.


La geología estudia la forma de las piedras y volcanes y la biología se ocupa de las formas de los seres vivos y de como ésta ha ido cambiando a lo largo del tiempo. Pero, ¿Cómo explicar los mecanismos que crean el aspecto exterior de la realidad que podemos percibir? ¿Y por qué existen las mismas estructuras tanto en los organismos vivos como en el mundo inanimado?

Observamos la Naturaleza y podemos contemplar formas armoniosas y elegantes, entendiendo que son cuerpos bellos y simétricos en todas sus versiones. Por ejemplo, a mí siempre me llamó la atención la simetría por traslación que se puede encontrar en la disposición de las hojas.
Si nos fijamos y analizamos como se van desarrollando hacia la extremidad de su rama, aparecen con la misma forma inicial. Un asimetría que está presente en los organismos que cuentan con una estructura en la que se repiten segmentos iguales, con los mismos aparatos y los mismos órganos, como el trilobites, fósil del Paleozoico (lombriz y sanguijuela), y algunas plantas.

En cambio la simetría por rotación se encuentra en los pétalos de una flor o en los tentáculos de una medusa: aunque sus cuerpos roten, permanecen iguales. No debemos olvidar la simetría bilateral que hace que los lados derecho e izquierdo sean iguales y se presenta en casi todos los animales, incluido nosotros. Pero es uniendo estos aspectos cuando se obtienen figuras realmente armoniosas. Si se trata de desplazamiento y rotación en un mismo plano hablamos de una espiral, mientras que en el espacio sería una hélice, aunque ambas se encuentran por todas partes en la naturaleza.
Las simetrías se generan mediante las fuerazas que actúan sobre los cuerpos, descritas por leyes rigurosas e inequívocas, como una fórmula matemática y dependen de la existencia de fuerzas distintas que actúan en diversas direcciones. Si éstas permanecen en equilibrio, no hay preferencia alguna hacia arriba o abajo, a la derecha o a la izquierda, y los cuerpos tenderán a ser perfectamente esféricos, como suele ocurrir en el caso de virus y bacterias. Además, cuando el aspecto no es el de una esfera perfecta, la Naturaleza hará todo lo posible para hacercarse a esta forma.
En todo esto, y, para que así ocurra, tiene que estar presente la Gravedad. Veamos:

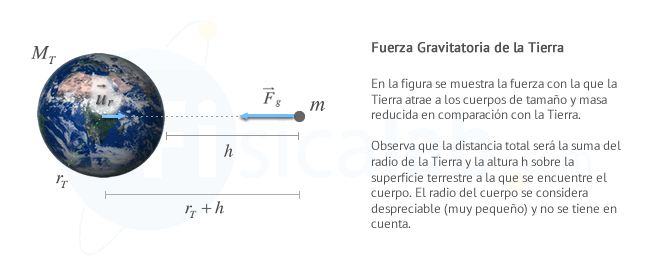
Parémonos un momento en la gravitación y generalicemos el concepto de simetría, ampliándolo a las fórmulas matemáticas. Veamos la fórmula de Newton, pero expresándola con palabras, de esta manera: la fuerza de atracción entre dos cuerpos es proporcional al producto de dos términos: el primero es la masa de un cuerpo dividido por su distancia al otro. El segundo término es la masa del otro cuerpo dividido por su distancia al primero.
Con símbolos matemáticos escribiríamos:
F![]() (M/d) × (m/d)
(M/d) × (m/d)
Es la misma fórmula de siempre, pero la hemos puesto así para visualizar que la gravitación se puede expresar con una fórmula bastante simétrica: los dos términos de la derecha de la ecuación son “casi” simétricos ¿no es verdad?
Este concepto más general de simetría es muy profundo, porque nos lleva a pensar que la Naturaleza y las leyes físicas que la describen también obedecen a las leyes de la simetría, igual que la materia, en sus manifestaciones externas, las obedece en muchos casos.
¿Sería posible que la simetría material tuviera un paralelismo en la abstracción intelectual que son las leyes físicas? Desde luego hace falta un esfuerzo mental considerable para pasar de lo material a lo intelectual, pero cuando se profundiza en ella, la conexión aparece.
En la naturaleza existen muchas cosas que nos pueden llevar a pensar en lo complejo que puede llegar a resultar entender cosas que, a primera vista, parecían sencillas. Me explico:

Fijémonos, por ejemplo, en una Flor de Girasol y en las matemáticas que sus semillas conllevan. Forman una serie de números en la que cada cifra es la suma de las dos precedentes (por ejemplo 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…) se denomina, en términos matemáticos, sucesión de Fibonacci, una ley que se cumple incluso en el mundo vegetal, como hemos podido comprobar en las semillas del girasol, dispuestas en espiral y que respetan ésta fórmula.

Todo lo que existe vibra, por lo cual tiene energía, esta vibración viaja a través del agua y los cristales hexagonales del agua helada , representa la fuerza vital de la madre naturaleza….
….la ausencia de cristales hexagonales es un indicio de que la fuerza vital de una determinada zona ha sido puesta en peligro enérgéticamente.
En el mundo inorgánico las leyes de la cristalización del agua congelada, determinadas por las fuerzas que actúan entre las moléculas, hacen que los cristales adopten formas que son infinitas y varían con respecto a un tema común: la estrella de seis puntas. Sin embargo, los planetas son esféricos porque han nacido en la nube primordial que rodeaba al Sol, atrayendo materia indeferentemente de todas partes.
Por otro lado, cuando la fuerza de la Gravedad actúa en una dirección y permite distinguir lo alto de lo bajo, los cuerpos asumen formas que gozan de simetría por rotación, en torno a un eje vertical, como las flores, los árboles, las medusas. Si este organismo presente ojos y boca sobre la parte anterior del cuerpo para alcanzar la comida antes que sus competidores (que es lo que sucede con los animales superiores) tenderá a mantener una correspondencia bilateral, lo que hace relativamente intercambiables derecha e izquierda.

¿Qué es la proporción divina o áurea?

La proporción divina es una representación gráfica de la sucesión de números de Fibonacci en forma de espiral. Leonardo Pisano, también conocido como Fibonacci, fue un matemático italiano; uno de sus descubrimientos, entre otros, fue la sucesión de Fibonacci. Esta sucesión matemática posteriormente dio lugar a la representación matemática de la proporción divina, también conocida como áurea.
La proporción divina no fue un descubrimiento de Fibonacci, de hecho se llevaba usando de forma constante desde antiguo. Se usó en la construcción de las pirámides egipcias, pasando a Grecia, Roma y el arte y arquitectura medievales y de ahí al Renacimiento Italiano. Incluso se han encontrado ejemplos de su uso en antiguas cerámicas de nativos americanos.
Mona lisa. La fama de esta pintura no se basa únicamente en la técnica empleada o en su belleza, sino también en los misterios que la rodean. Y, también, en la perfección simétrica que está ahí presente.
Los seres humanos (su exterior) somos buenos ejemplos de esto. Tenemos una casi igualdad entre las dos partes de nuestro cuerpo que se obtendrían dividiéndolo por una línea que pasa por el centro de la nariz y por el centro del ombligo. La figura de arriba muestra el famoso estudio sobre la simetría del cuerpo humano de Leonardo da Vinci.

¿Cómo podemos llegar a la simetría presente en las manchas del leopardo? Pues, tiene su explicación científica, tanto en este animal como en otros felinos, ocurre ésta particularidad de ser poseedores de una piel exterior que los singulariza de otros por su perfecta simetría y belleza de las formas en su conjunto.
Claro que, en la Naturaleza, nada ocurre porque sí, todo tiene su por qué, y, todo lo que en ella podemos contemplar posee una funcionalidad que está directamente relacionada con su mecánica, con el medio en el que habita, con lo que el Universo espera que haga en su medio y, para ello, dota a cada figura con aquellos “trajes” que mejor les permita realizar aquello para lo que están destinados.

Simetría en las galaxias espirales
Vamos a generalizar un paso más el concepto de simetría, planteándonos ahora si es posible que una ley física se cumpla en cualquier lugar. ¿En cualquier lugar… de dónde?, ¿de nuestra ciudad?, ¿de nuestro planeta? No: del universo. Una ley que fuera válida en cualquier lugar del universo sería una ley simétrica respecto al espacio. Se cumpliría dondequiera que se hiciese un experimento para comprobarla.
Fíjense que nuestra idea de simetría se va haciendo más compleja y más profunda. Ahora no nos detenemos en ver si la forma material de un objeto es simétrica, ni de si la escritura de una fórmula matemática es simétrica. Ahora nos preguntamos si una ley física es válida en todo el Universo.
La otra simetría interesante para una ley física es la que se refiere al tiempo. Cierta ley física se cumple ahora; ¿antes también?, ¿se cumplirá pasado algún tiempo? Una ley que fuera cierta en cualquier instante de la historia del universo sería una ley simétrica respecto al tiempo.
Lo que ahora nos preguntamos es: ¿son simétricas o no las leyes de la física?
Hasta donde alcanzan nuestras medidas, las leyes físicas (y, por tanto, la interacción gravitatoria) sí son simétricas respecto al espacio y respecto al tiempo. En cualquier lugar y momento temporal del universo, la Naturaleza se comporta igual que aquí y ahora en lo que se refiere a estas leyes.
Esta simetría es un arma muy poderosa para investigar hacia el pasado y hacia el futuro, ya que nos permite suponer (y, en la medida en que confiemos en la seguridad de la simetría, conocer) condiciones locales donde jamás podremos llegar por la distancia espacial y temporal que nos separa de muchas partes del universo. Así, por ejemplo, gracias a esta simetría, podemos calcular que el Sol lleva 5.000 millones de años produciendo energía y que le quedan, probablemente, otros 5.000 millones hasta que consuma toda su masa. Esto lo podemos aventurar suponiendo que en ese enorme tramo de 5.000 + 5.000 = 10.000 millones de años las leyes físicas que determinan los procesos mediante los cuales el Sol consume su propia masa como combustible (las reacciones nucleares que le permiten producir energía), fueron, son y serán las mismas aquí en el Brazo de orión donde nos encontramos como en los arrabales de la Galaxia Andrómeda donde luce una estrella como nuestro Sol que, también envía luz y calor a sus planetas circundantes, y, por muy lejos que podamos mirar, siempre veremos lo mismo.

Por tanto, en cierto modo, la simetría se vuelve tan importante o más que la propia ley física. La simetría está presente n todas partes, en todo0 el Universo contemplamos imagines simétricas.
La regularidad de las formas de la Naturaleza se refleja incluso en la cultura humana, que desde siempre intenta inspirarse en el mundo natural para conformar su propio mundo. Existen hélices en las escaleras de palacios, castillos y minaretes y en las decoraciones de esculturas y columnas. Las espirales abundan en los vasos, en los bajorrelieves, en los cuadros, en las esculturas en los collares egipcios, griegos, celtas, precoolombinos e hindúes e, incluso, en los tatuajes con los que los maoríes neozelandeses se decoran el rostro.

La búsqueda de la perfección geométrica y de las propiedades matemáticas pueden ser también una guía importante en el estudio científico del mundo. Paul Dirac, una de los padres de la moderna mecánica cuántica, solía decir que “si una teoría es bella desde el punto de vista matemático, muy probablemente es también verdadera”.
A todo esto, no debemos olvidar que todo, sin excepción, en nuestro Universo, está sometido a la Entropía que nos trae el paso inexorable de eso que llamamos “Tiempo”, y que, convierte perfectas simetrías de joven belleza, en deteriorados objetos o entidades que, nos viene a recordar que nada es perpetuo, que todo pasa y se transforma.

¿Tendrá ella esa clase de belleza oculta?
Un dolor que llevo dentro de mí es el no poder contemplar la verdadera belleza que, estando presente en los seres vivos inteligentes, en la mayoría de los casos, se nos queda oculta a nuestra percepción, toda vez que, esa clase de belleza que no podemos ver pero sí percibir, sólo la podemos captar con el trato y la convivencia y, verdaderamente, tengo que admitir que, algunas bellezas que he tenido la suerte de poder “ver” con los ojos del espíritu, llegan a ser segadoras, deslumbrantes, su explendor es muy superior al de la estrella más brillante del cielo, y, seguramente (estoy seguro) como a muchos de ustedes les pasa, tengo la suerte de tenerla junto a mí desde hace muchos años. y, si pienso en ello en profundidad y detenimiento, no tengo más remedio que concluir que es ese brillo y esplendor el que me da la fuerza para seguir cada dia en la dura lucha que nos ha tocado participar.
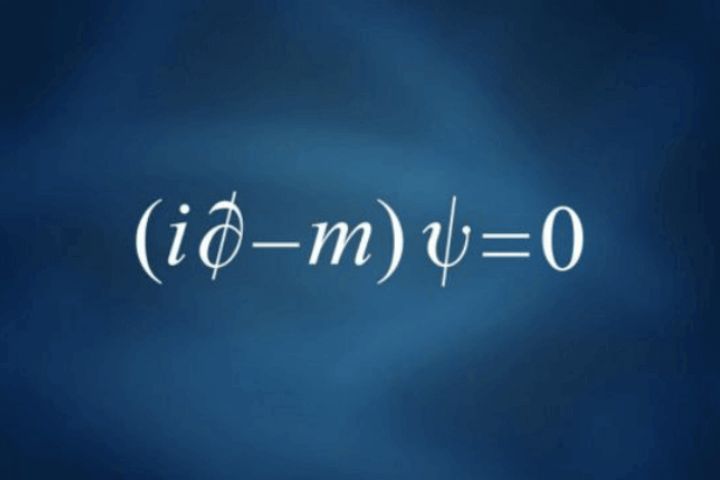
“La ecuación de Dirac para el electrón la podemos escribir de la siguiente forma: (βmc2–icℏα1∂∂x−icℏα2∂∂y–icℏα3∂∂z+V(x,y,z))ψ(x,t)=iℏ∂ψ(∂ son las matrices de Pauli. En las expresiones anteriores ℏ es la constante de Planck, m la masa del electrón y c la velocidad de la luz.”
¡Sí que es importante la Belleza! Dirac tenía toda la razón.
Emilio Silvera Vázquez
Ago
1
¿La Naturaleza? ¡Simetría dentro de la Diversidad!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Simetrías ~
Clasificado en Simetrías ~
 Comments (0)
Comments (0)


Nuestro planeta visto desde el Espacio
Nuestro mundo, aunque en la Galaxia existan muchos como él (que no los hemos podido encontrar), es un lugar privilegiado que conforma un Ecosistema superior en su conjunto formado por muchos ecosistemas locales aislados los unos de los otros y sin embargo, todos conexionados. La Diversidad de regiones diferentes que existen dentro del mismo planeta es asombrosa y, lo mismo nos podemos encontrar en un lugar como ese que vemos arriba, o en una isla paradisíaca, una selva, un desierto, o perdidos en un inmenso y embravecido océano, en la ventisca de nieve de inmensas montañas y, también, en grutas enormes en las profundidades del planeta.
“”La posición de la Tierra en el sistema solar también es privilegiada, ya que tiene un cuerpo gigante, Júpiter, que la protege de cometas y asteroides. Tiene, además, una atmósfera casi única que hace posible la vida, un efecto invernadero y un campo magnético que la protege de las radiaciones.”
Pero todos esos climas diferentes son el resultado de la diversidad y, en cada uno de esos lugares ocurren cosas y, la vida, aunque parezca imposible, está allí presente. Es la consecuencia de que el planeta Tierra esté situado en la zona habitable del Sol, ni demasiado cerca para que la vida perezca achicharrada, ni demasiado lejos para que resulte congelada por el frío. Aquí el agua discurre líquida y cantarina por multitud de lugares y hace posible que, entre el preciado líquido y los rayos del Sol que nos envían la luz y el calor necesarios para la fotosíntesis y la vida… ¡Podamos estar aquí!
“El electromagnetismo es la rama de la física que estudia las relaciones entre los fenómenos eléctricos y magnéticos, es decir, entre el campo magnético y la corriente eléctrica.”
Fuente: https://concepto.de/electromagnetismo/#ixzz5sIhuRCgE
Todos sabemos que la materia en nuestro Universo adopta muchas formas distintas: Galaxias de estrellas y mundos que, en alguna ocasión, pueden incluso tener seres vivos y algunos han podido evolucionar hasta adquirir la consciencia. Sin embargo, no me quería referir a eso que es bien sabido por todos, sino que, trato de pararme un poco sobre una curiosa propiedad que la materia tiene en algunas ocasiones y que, la Naturaleza se empeña en repetir una y otra vez: ¡La Simetría!
Las Galaxias espirales, la redondez de los mundos, las estrellas del cielo, los árboles y las montañas, los ríos y los océanos, las especies animales (incluida la nuestra) que, se repiten una y otra vez y, en general, salvando particularidades, todas repiten un patrón de simetría.
Recuerdo aquí aquel pensamiento de Paul Valery en el que nos decía:
“El Universo está construido según un plan cuya profunda simetría está presente de algún modo en la estructura interna de nuestro intelecto.”

La Naturaleza está llena de simetrías
La simetría es una propiedad universal tanto en la vida corriente, como desde un punto de vista matemático desde el quehacer de la Física Teórica. En realidad, lo que observamos en la vida corriente es siempre lo repetitivo, lo simétrico, lo que se puede relacionar entre sí por tener algo común. Es siempre lo mismo dentro de una inmensa diversidad formada por grupos iguales.
En un sentido dinámico, la simetría podemos entenderla como lo que se repite, lo reiterativo, lo que tiende a ser igual. Es decir, los objetos que, por mantener la misma geometría, son representativos de otros objetos. En el Caos matemático encontramos concepción de la simetría en el mundo los fractales. Sin embargo, la simetría es mucho más. Hay distintas maneras de expresarla: “Conjunto de invariancias de un sistema”, podría ser una de ellas. Al aplicar una transformación de simetría sobre un sistema, el sistema queda inalterado, la simetría es estudiada matemáticamente usando teoría de grupos. Algunas de las simetrías son directamente físicas. Algunos ejemplos son las reflexiones y las rotaciones en las moléculas y las translaciones en las redes cristalinas.

Aquí hay mucho más de lo que a simple vista parece.

La divina proporción aurea, el nñume3ro de oro (PHI)
Los físicos teóricos también se guían en sus investigaciones por motivaciones estéticas tanto como racionales. Poincaré escribió: “Para hacer ciencia, es necesario algo más que la pura lógica”. Él identificó ese elemento adicional como la intuición, que supone “el sentido de la belleza matemática”. Heisenberg hablaba de “la simplicidad y belleza de los esquemas matemáticos que la Naturaleza nos presenta”.

La simetría está presente por todas partes y, cada objeto, tiene la suya que siempre, está relacionada con la de otro de la misma especie. Hay simetrías que en física incluye todos los rasgos de un sistema físico que exhibe propiedades de la simetría – eso es, que bajo ciertas transformaciones, aspectos de esos sistemas son “incambiables”, de acuerdo a una observación particular. Una simetría de un sistema físico es un rasgo físico o matemático de un sistema que es preservado sobre cierto cambio.
En matemática, una transformación es un operador aplicado a una función tal que bajo esa transformación, ciertas operaciones sean simplificadas. En ejemplo, en la aritmética cuando se busca un algoritmo de números, el proceso de búsqueda es reducido a la suma de los algoritmos de cada factor.

Por ejemplo, veamos la invariancia de escala: En un recipiente con agua a punto de hervor, las burbujas de vapor, nucleadas en el fondo del recipiente, crecen, se liberan, y fluctúan hasta la superficie de donde se escapan para la atmósfera. A la temperatura de ebullición, el agua existe al mismo tiempo en dos fases distintas – líquido y gas – y a medida que las burbujas se forman las dos fases se separan en el espacio. Si cerramos el recipiente la temperatura de ebullición aumenta, como en una olla a presión. A medida que la presión aumenta, el sistema llega al punto crítico, donde las propiedades del líquido y del gas se vuelven idénticas. Por encima de esa temperatura, en el régimen supercrítico, dejan de existir dos fases distintas y existe apenas un fluido homogéneo.

Cerca del punto crítico, la materia fluctúa sin límites. Burbujas y gotas, unas tan pequeñas como unos cuantos átomos, otras tan grandes como el recipiente, aparecen y desaparecen, se unen y se separan. Exactamente en el punto crítico la escala de las mayores fluctuaciones divergen, pero el efecto de las fluctuaciones en escalas menores no es despreciable. La distribución de las fluctuaciones es invariable para transformaciones de escala.
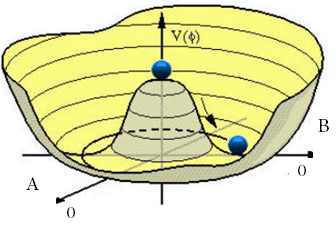
De la figura se deduce que la teoría tiene una “simetría interna”: la figura no cambia cuando hacemos rotaciones en el plano definido por A y B. La invariancia es definida matemáticamente por transformaciones que dejan magnitudes sin cambio. Por ejemplo, la distancia entre dos puntos de un sólido que se mueve, pero no se deforma.
Simetrías locales y globales
Una simetría global es una simetría que sostiene todos los puntos en el tiempo-espacio bajo consideración, a diferencia de la simetría local que solo sostiene a un subconjunto de puntos.
Un lagrangiano

La mayoría de las teorías físicas son descritas por lagrangianos (En física, un lagrangiano es una función matemática a partir del cual se pueden derivar la evolución temporal, las leyes de conservación y otras propiedades importantes de un sistema físico) que son invariantes bajo ciertas transformaciones, cuando las transformaciones son realizadas en diferentes puntos del espacio-tiempo y están relacionadas linealmente – ellas tienen simetría global.
Por ejemplo, en toda teoría cuántica la fase global de una función de onda es arbitraria y no representa algo físico. Consecuentemente, la teoría es invariante bajo a cambio global de fases (Agregando una constante a la fase de todas las funciones de onda, en todos lados); esto es una simetría global. En la electrodinámica quántica, la teoría es también invariante bajo un cambio local de fase, es decir, que se puede alterar la fase de todas las funciones de onda tal que la alteración sea diferente en cada punto del espacio-tiempo. Esto es una simetría local.

También se habla de ruptura de simetrías temporales en la física de partículas.
Los físicos creen también que están en el camino correcto porque, de algún modo que no pueden explicar, tienen la convicción de que son correctas, y las ideas de simetría son esenciales para esa intuición. Se presiente que es correcto que ningún lugar del Universo es especial comparado con cualquier otro lugar del Universo, así que los físicos tienen la confianza de que la simetría de traslación debería estar las simetrías de las leyes de la Naturaleza. Se presiente que es correcto que ningún movimiento a velocidad constante es especial comparado con cualquier otro. De modo que los físicos tienen confianza en que la relatividad especial, al abrazar plenamente la simetría entre todos los observadores con velocidad constante, es una parte esencial de las leyes de la Naturaleza.
Se dice que esta ecuación de Euler es la más bella conocida. Aunque son muchas las ecuaciones que podríamos traer aquí y que son de todos conocidas y han quedado como símbolos en la historia de las matemáticas, la de Euler, es posible que por su elegancia y simplicidad, le pueda ganar a las demás en belleza. Ahí, en ese sencillo conjunto, los números más significativos de las matemáticas se abrazan: o, 1, e, π, y la unidad imaginaria i .
Si se fijan en la fórmula, en ella aparecen los 5 números más importantes en la historia de las matemáticas. El 0 y el 1 que, entre otras aportaciones a esta disciplina, son famosos por ser elementos neutros y, por lo tanto, indispensables en las operaciones de suma y producto; los números π y e, posiblemente, los dos irracionales más famosos (junto con φ, la razón aúrea) que existen (y que nos permiten hacer el chiste aquel de que la parte más irracional de nuestro cuerpo es el pi-e); y la unidad imaginaria, i, cuyo valor es
La BBC Earth le preguntó a matemáticos y físicos qué ecuaciones piensan que son las más hermosas. ¡Aquí las 12 elegidas! las ecuaciones que ellos piensan son las más bonitas.

La ecuación de Dirac arriba. La ecuación fue descubierta a finales de los años 20 por el físico Paul Dirac, y juntó dos de las ideas más importantes de la ciencia: la mecánica cuántica, que describe el comportamiento de objetos muy pequeños; y la teoría especial de Einstein de la relatividad, que describe el comportamiento de objetos en movimiento rápido.
La ecuación fue descubierta por el físico Paul Dirac a finales de los años 20 y junta la mecánica cuántica y la teoría especial de Einstein de la relatividad, que describe el comportamiento de objetos en movimiento rápido. En otras palabras, explica cómo las partículas se comportan cuando viajan a casi la velocidad de la luz.
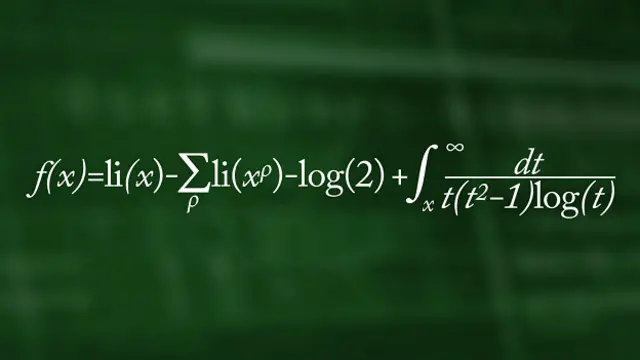
El matemático Bernhard Riemann publicó esta ecuación en 1859
Permite calcular los números primos por debajo de un número dado. “Son los números más básicos e importantes en el corazón del mundo de la matemática. Pero sorprendentemente, a pesar de más de 2000 años de investigación, todavía no los entendemos”, explica Marcus du Sautoy de la universidad de Oxford.
Pi
Pi es la ecuación de la circunferencia, la relación entre la circunferencia y el diámetro de un círculo. Además es un número irracional, lo que significa que los dígitos pueden continuar indefinidamente sin que se repitan.
En uno de los artículos científicos revolucionarios de Albert Einstein publicado en 1905, se introdujo el concepto de E=mc2, donde “E” es energía, “m” es masa y “c” es la velocidad de la luz en el vacío.[1]Desde entonces, E=mc2 se ha convertido en una las ecuaciones más famosas del mundo. Incluso las personas que no tienen conocimiento de física al menos han oído sobre esta ecuación y saben la enorme influencia que tiene en el mundo en que vivimos. Sin embargo, la mayoría de las personas no saben exactamente qué es lo que significa. En términos simples, la ecuación representa la equivalencia entre la masa y la energía; básicamente indica que ambas son solo dos formas diferentes de la misma cosa.[2]Esta simple ecuación ha alterado la forma en la que pensamos sobre la energía y nos ha permitido crear un gran número de avances tecnológicos.
“La ecuación de Euler-Lagrange fue desarrollada en 1750 por Euler y Lagrange como solución al problema de la tautócrona (caso general de la braquistócrona): consiste en determinar la curva de la trayectoria que describiría el descenso en la que una partícula con masa cae a cierto punto, en un tiempo dado, independiente de su posición inicial.
Lagrange resolvería el problema en 1755 y enviaría la solución a Euler. Ambos desarrollarían aún más el método de Lagrange y lo aplicarían a problemas de mecánica; cosa que a su vez conduciría a formular por vez primera la mecánica lagrangiana. Dicha correspondencia también desembocaría en el desarrollo del cálculo de variaciones, un término acuñado por el mismo Euler en 1766.”
Esta ecuación se utiliza para analizar todo. “Más que una ecuación, es una receta para generar una infinita variedad de posibles leyes de física”, comenta Andrew Pontzen de la University College London.
La entidad de
En matemáticas, la identidad de Euler es la igualdad: Función exponencial ez puede definirse como el límite de una secuencia (1 + z/N)N, con N tendiendo a infinito, y así e iπ es el límite de (1 + iπ/N)N.
La ecuación de onda.
El autor de la ecuación matemática más famosa es Leonhard Euler, de ahí que lleve su nombre: la identidad de Euler, llamada «identidad» porque en ella solo existen números. Aunque en la fórmula veamos letras, estas representan en realidad números.
La identidad más famosa de las matemáticas. La Identidad de Euler es la fórmula más famosa de las matemáticas, ya que liga los cinco números más famosos de la matemática e, i, π , 1 y 0. ¡Sólo falta Φ
Demostró el último teorema de Fermat para n = 3, donde introdujo cálculo con números algebraicos. Se puede afirmar que el análisis matemático comienza con Euler.
La fórmula de Euler es eⁱˣ=cos(x)+i⋅sin(x), y la identidad de Euler es e^(iπ)+1=0. Observa cómo se obtienen estas relaciones por medio de las series de Maclaurin de cos(x), sin(x) y eˣ. ¡Estos son algunos de los resultados más sorprendentes de las matemáticas!
“La belleza de la ecuación de la onda se manifiesta de muchas formas”, explica Ian Stewart de la universidad de Warwick del Reino Unido. Se aplica a todo tipo de ondas, desde las de agua a las de sonido y vibraciones. Incluso a las ondas de luz y radio.
Este teorema tiene más usos de los que uno se imagina, calcula la probabilidad que un evento (A) sea real, dado que otro evento (B) también lo es. Tiene muchos usos, como para detectar fallas de vigilancia, defensa militar, operaciones de búsqueda y rescate, en escáneres médicos en incluso para filtros de correos electrónicos no deseados.
Pasamos a la ecuación de campo de Einstein
Tensor de curvatura de Einstein, que se forma a partir de derivadas segundas del tensor métrico gμν
Tensor momento-energía c Velocidad de la luz G Constante de la gravitación universal
Esta ecuación es en realidad un sumario de diez ecuaciones. Katie Mack, de la universidad de Melbourne en Australia, explica que estas fórmulas cambiaron completamente cómo entendemos la naturaleza y evolución del Universo. La ecuación de Einstein nos puede decir cómo nuestro universo ha cambiado con el tiempo, y ofrece un vistazo de los primeros momentos de la creación.
Es un prodigio de la Mente humana
Dirac nos hablaba de ecuaciones bellas. La estética es, evidentemente, subjetiva, y la afirmación de que los físicos buscan la belleza en sus teorías tiene sentido sólo si podemos definir la belleza. Afortunadamente, esto se puede , en cierta medida, pues la estética científica está iluminada por el sol central de la simetría.
La Naturaleza nos la muestra por todas partes
La simetría es un concepto venerable y en modo alguno inescrutable y no podemos negar que tiene muchas implicaciones en la Ciencia, en las Artes y sobre todo, ¡en la Naturaleza! que de manera constante nos habla de ella. Miremos donde miremos…¡allí está!

El físico chino-norteamericano Chen Ning Yang ganó el Nóbel de Física por su en el desarrollo de una teoría de campos basada en la simetría y, aún afirmaba: “No comprendemos todavía el alcance del concepto de simetría”. Es lógico pensar que, si la Naturaleza emplea la simetría en sus obras, la razón debe estar implicada con la eficacia de los sistemas simétricos.
En griego, la palabra simetría significa “la misma medida” (syn significa “juntos”, como en sinfonía, una unión de sonidos, y metrón, “medición”); así su etimología nos informa que la simetría supone la repetición de una cantidad medible. Pero la simetría los griegos, también significaba la “la debida proporción”, lo que implicaba que la repetición involucrada debía ser armoniosa y placentera, como de hecho, resultan ser en las imágenes que arriba contemplamos. Asi, la Naturaleza nos está indicando que una relación simétrica debe ser juzgada por un criterio estético superior.

Humo simétrico
Muchos de nosotros, la mayoría, conocimos la simetría en sus manifestaciones geométricas de aquellas primeras clases en la Escuela Elemental, más tarde en el arte y, finalmente, la pudimos percibir en la Naturaleza, en el Universo y en nosotros mismos que, de alguna manera, somos de ese Universo de simetría.
Los planetas son esféricos y, por ejemplo, tienen simetría de rotación. Lo que quiere indicar es que poseen una característica -en caso, su perfil circular- que permanece invariante en la transformación producida cuando la Natuiraleza los hace rotar. Las esferas pueden Hacerse rotar en cualquier eje y en cualquier grado sin que cambie su perfil, lo cual hace que sea más simétrica.

La clave de la belleza está en la simetría
La simetría por rotación se encuentra en los pétalos de una flor o en los tentáculos de una medusa: aunque sus cuerpos roten, permanecen iguales. La simetría bilateral que hace que los lados derecho e izquierdo sean iguales y se presenta en casi todos los animales, incluido nosotros. Pero es uniendo estos aspectos se obtienen figuras realmente armoniosas. Si se trata de desplazamiento y rotación en un mismo plano hablamos de una espiral, mientras que en el espacio sería una hélice, aunque ambas se encuentran por todas partes en la naturaleza.
Las simetrías se generan mediante las fuerzas que actúan sobre los cuerpos, descritas por leyes rigurosas e inequívocas, como una fórmula matemática y dependen de la existencia de fuerzas distintas que actúan en diversas direcciones. Si éstas permanecen en equilibrio, no hay preferencia alguna hacia arriba o abajo, a la derecha o a la izquierda, y los cuerpos tenderán a ser perfectamente esféricos, como suele ocurrir en el caso de virus y bacterias, las estrellas y los mundos… las galaxias. Además, cuando el aspecto no es el de una esfera perfecta, la Naturaleza hará todo lo posible para acercarse a esta.

La simetría también están presentes en nuestros cerebros
¿Sería posible que la simetría material tuviera un paralelismo en la abstracción intelectual que son las leyes físicas? luego hace falta un esfuerzo mental considerable para pasar de lo material a lo intelectual, pero cuando se profundiza en ellla, la conexión aparece. En la naturaleza existen muchas cosas que nos pueden llevar a pensar en lo complejo que puede llegar a resultar entender cosas que, a primera vista, parecían sencillas.
Me explico:

Fijémonos, por ejemplo, en una Flor de Girasol y en las matemáticas que sus semillas conllevan. Forman una serie de números en la que cifra es la suma de las dos precedentes (por ejemplo 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…) se denomina, en términos matemáticos, sucesión de Fibonacci, una ley que se cumple incluso en el mundo vegetal, como hemos podido comprobar en las semillas del girasol, dispuestas en espiral y que respetan ésta fórmula. La podemos ver por todas partes.

Lo mismo ocurre con otros ejemplares de la diversidad del mundo de las plantas
En el mundo inorgánico las leyes de la cristalización del agua congelada, determinadas por las fuerzas que actúan entre las moléculas, hacen que los cristales adopten formas que son infinitas y varían con respecto a un tema común: la estrella de seis puntas. Sin embargo, los planetas son esféricos porque han nacido en la primordial que rodeaba al Sol, atrayendo materia indiferentemente de todas partes.





Claro que, en la Naturaleza, nada ocurre porque sí, todo tiene su por qué, y, todo lo que en ella podemos contemplar posee una funcionalidad que está directamente relacionada con su mecánica, con el medio en el que habita, con lo que el Universo espera que haga en su medio y, para ello, dota a figura con aquellos “trajes” que mejor les permita realizar aquello para lo que están destinados.
Vamos a generalizar un paso más el concepto de simetría, planteándonos si es posible que una ley física se cumpla en cualquier lugar. ¿En cualquier lugar… de dónde?, ¿de nuestra ciudad?, ¿de nuestro planeta? No: del universo. Una ley que fuera válida en cualquier lugar del universo sería una ley simétrica respecto al espacio. Se cumpliría dondequiera que se hiciese un experimento para comprobarla.

La simetría de las galaxias espirales
Fíjense que nuestra idea de simetría se va haciendo más compleja y más profunda. no nos detenemos en ver si la forma material de un objeto es simétrica, ni de si la escritura de una fórmula matemática es simétrica. Ahora nos preguntamos si una ley física es válida en todo el Universo.
La otra simetría interesante para una ley física es la que se refiere al tiempo. Cierta ley física se cumple ; ¿antes también?, ¿se cumplirá pasado algún tiempo? Una ley que fuera cierta en cualquier instante de la historia del universo sería una ley simétrica respecto al tiempo.

Lo que nos preguntamos es: ¿son simétricas o no las leyes de la física?
Hasta donde alcanzan nuestras medidas, las leyes físicas (y, por tanto, la interacción gravitatoria) sí son simétricas respecto al espacio y respecto al tiempo. En cualquier lugar y momento temporal del universo, la Naturaleza se comporta igual que aquí y ahora en lo que se refiere a estas leyes.

Todas las especies son simétricas entre sí
Esta simetría es un arma muy poderosa para investigar hacia el pasado y hacia el futuro, ya que nos permite suponer (y, en la medida en que confiemos en la seguridad de la simetría, conocer) locales donde jamás podremos llegar por la distancia espacial y temporal que nos separa de muchas partes del universo. Así, por ejemplo, gracias a esta simetría, podemos calcular que el Sol lleva 5.000 millones de años produciendo energía y que le quedan, probablemente, otros 5.000 millones hasta que consuma toda su masa. Esto lo podemos aventurar suponiendo que en ese enorme tramo de 5.000 + 5.000 = 10.000 millones de años las leyes físicas que determinan los procesos mediante los cuales el Sol consume su propia masa como combustible (las reacciones nucleares que le permiten producir energía), fueron, son y serán las mismas aquí en el Brazo de Orión donde nos encontramos como en los arrabales de la Galaxia Andrómeda donde luce una estrella como nuestro Sol que, también envía luz y calor a sus planetas circundantes, y, por muy lejos que podamos mirar, siempre veremos lo mismo.
Por tanto, en cierto modo, la simetría se vuelve tan importante o más que la propia ley física.

La regularidad de las formas de la Naturaleza se refleja incluso en la cultura humana, que desde siempre intenta inspirarse en el mundo natural conformar su propio mundo. Existen hélices en las escaleras de palacios, castillos y minaretes y en las decoraciones de esculturas y columnas. Las espirales abundan en los vasos, en los bajorrelieves, en los cuadros, en las esculturas en los collares egipcios, griegos, celtas, precolombinos e hindúes e, incluso, en los tatuajes con los que los maoríes neozelandeses se decoran el rostro.

¿Tenía en mente Leonardo la proporción áurea a la hora de realizar su obra maestra? Afirmarlo resultaría aventurado. Menos polémico es aseverar que el genio florentino concedía gran importancia a la relación entre la estética y la matemática. Dejaremos la cuestión en el aire por el momento, no sin antes mencionar que Leonardo realizó las ilustraciones de una obra de contenido estrictamente matemático, escrita por su buen amigo Luca Pacioli, llamada “De divina proportione”, es decir, “La divina proporción”.
La proporción aurea
La búsqueda de la perfección geométrica y de las propiedades matemáticas pueden ser una guía importante en el estudio científico del mundo. Paul Dirac, una de los padres de la moderna mecánica cuántica, solía decir que “si una teoría es bella desde el punto de vista matemático, muy probablemente es también verdadera”.
A todo esto, no debemos olvidar que todo, sin excepción, en nuestro Universo, está sometido a la Entropía que nos trae el paso inexorable de eso que llamamos “Tiempo”, y que, convierte perfectas simetrias de joven belleza, en deteriorados objetos o entidades que, nos viene a recordar que nada es perpetuo, que todo pasa y se transforma. Claro que, de alguna manera, todo vuelve a resurgir.

La Belleza más valiosa no la podemos ver. ¡Vive en el interior!
Un dolor que llevo dentro de mí es el no poder contemplar la verdadera belleza que estando presente en los seres vivos inteligentes, en la mayoría de los casos, se nos queda oculta a nuestra percepción, toda vez que esa clase de belleza, que no podemos ver pero sí percibir, sólo la podemos captar con el trato y la convivencia y, verdaderamente, tengo que admitir que, algunas bellezas que he tenido la suerte de poder “ver con los ojos del espíritu”, llegan a ser segadoras, deslumbrantes, su esplendor es muy superior al de la estrella más brillante del cielo, y, seguramente (estoy seguro) como a muchos de ustedes les pasa, tengo la suerte de tenerla junto a mí desde hace muchos años. y, si pienso en ello en profundidad y detenimiento, no tengo más remedio que concluir que es ese brillo y esplendor el que me da la fuerza para seguir cada dia en la dura lucha que nos ha participar.
¡Sí que es importante la Belleza! Dirac tenía toda la razón. Y, no digamos las Simetrías que nos señala el dedo de la Naturaleza el camino a seguir a muchos físicos que quieren desvelar sus secretos.
Emilio Silvera V.
Abr
3
¿La Naturaleza? ¡Simetría dentro de la Diversidad!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Simetrías ~
Clasificado en Simetrías ~
 Comments (4)
Comments (4)

Nuestro mundo, aunque en la Galaxia existan muchos parecidos, no por ello tenemos que dejar de reconocer que, de alguna manera es, un lugar privilegiado que conforma un Ecosistema superior en su conjunto formado por muchos ecosistemas locales aislados los unos de los otros y sin embargo, todos conexionados. La Diversidad de regiopnes diferentes que existen dentro del mismo planeta es asombroso y, lo mismo nos podemos encontrar en un lugar como ese que vemos arriba, o en una isla paradisíaca, una selva, un desierto, o perdidos en un inmenso y embravecido océano, en la ventisca de nieve de inmensas montañas y, también, en grutas enormes en las profundidades del planeta.

Pero todos esos climas diferentes son el resultado de la diversidad y, en cada uno de esos lugares ocurren cosas y, la vida, aunque parezca imposible, está allí presente. Es la consecuencia de que el planeta Tierra esté situado en la zona habitable del Sol, ni demasiado cerca para que la vida perezca achicharrada, ni demasiado lejos para que resulte congelada por el frío. Aquí el agua discurre líquida y cantarina por multitud de lugares y hace posible que, entre el preciado líquido y los rayos del Sol que nos envían la luz y el calor necesarios para la fotosíntesis y la vida… ¡Podamos estar aquí!
Hemos llegado a un nivel muy aceptable de conocimientos y, nos permite hablar de cuestiones complejas como estas:
Todos sabemos que la materia en nuestro Universo adopta muchas formas distintas: Galaxias de estrellas y mundos que, en alguna ocasión, pueden incluso tener seres vivos y algunos han podido evolucionar hasta adquirir la consciencia. Sin embargo, no me quería referir a eso que es bien sabido por todos, sino que, trato de pararme un poco sobre una curiosa propiedad que la materia tiene en algunas ocasiones y que, la Naturaleza se empeña en repetir una y otra vez: ¡La Simetría!
Las Galaxias espirales, la redondez de los mundos, las estrellas del cielo, los árboles y las montañas, los ríos y los océanos, las especies animales (incluída la nuestra) que, se repiten una y otra vez y, en general, salvando particularidades, todas repiten un patrón de simetría.
Recuerdo aquí aquel pensamiento de Paul Valery en el que nos decía:
“El Universo está construido según un plan cuya profunda simetría está presente de algún modo en la estructura interna de nuestro intelecto.”

La Naturaleza está llena de simetrías
La simetría es una propiedad universal tanto en la vida corriente, como desde un punto de vista matemático desde el quehacer de la Física Teórica. En realidad, lo que observamos en la vida corriente es siempre lo repetitivo, lo simétrico, lo que se puede relacionar entre sí por tener algo común. Es siempre lo mismo dentro de una inmensa diversidad formada por grupos iguales.

Las matemáticas nos revelan el arte de la simetría
En un sentido dinámico, la simetría podemos entenderla como lo que se repite, lo reiterativo, lo que tiende a ser igual. Es decir, los objetos que, por mantener la misma geometría, son representativos de otros objetos. En el Caos matemático encontramos concepción de la simetría en el mundo los fractales. Sin embargo, la simetría es mucho más. Hay distintas maneras de expresarla: “Conjunto de invariancias de un sistema”, podría ser una de ellas. Al aplicar una transformación de simetría sobre un sistema, el sistema queda inalterado, la simetría es estudiada matemáticamente usando teoría de grupos. Algunas de las simetrías son directamente físicas. Algunos ejemplos son las reflexiones y las rotaciones en las moléculas y las translaciones en las redes cristalinas.

Aquí hay mucho más de lo que a a simple vista parece. La figura se conoce como “la sucesión de Fibonacci” que está presente en la naturaleza. Se trata de una serie infinita de números naturales, iniciada con los números 0 y 1, y a partir de aquí, cada elemento es la suma de los dos anteriores, y cada uno de ellos es conocido como número de Fibonacci:
Los físicos teóricos también se guían en sus investigaciones por motivaciones estéticas tanto como racionales. Poincaré escribió: “Para hacer ciencia, es necesario algo más que la pura lógica”. Él identificó ese elemento adicional como la intuición, que supone “el sentido de la belleza matemática”. Heisenberg hablaba de “la simplicidad y belleza de los esquemas matemáticos que la Naturaleza nos presenta”.
La simetría está presente por todas partes y, cada objeto, tiene la suya que siempre, está relacionada con la de otro de la misma especie. Hay simetrías que en física incluye todos los rasgos de un sistema físico que exhibe propiedades de la simetría – eso es, que bajo ciertas transformaciones, aspectos de esos sistemas son “incambiables”, de acuerdo a una observación particular. Una simetría de un sistema físico es un rasgo físico o matemático de un sistema que es preservado sobre cierto cambio.
En matemática, una transformación es un operador aplicado a una función tal que bajo esa transformación, ciertas operaciones sean simplificadas. En ejemplo, en la aritmética cuando se busca un algoritmo de números, el proceso de búsqueda es reducido a la suma de los algoritmos de cada factor.
Por ejemplo, veámos la invariancia de escala: En un recipiente con agua a punto de hervor, las burbujas de vapor, nucleadas en el fondo del recipiente, crecen, se liberan, y fluctúan hasta la superficie de donde se escapan para la atmósfera. A la temperatura de ebullición, el agua existe al mismo tiempo en dos fases distintas – líquido y gas – y a medida que las burbujas se forman las dos fases se separan en el espacio. Si cerramos el recipiente la temperatura de ebullición aumenta, como en una olla a presión. A medida que la presión aumenta, el sistema llega al punto crítico, donde las propiedades del líquido y del gas se vuelven idénticas. Por encima de esa temperatura, en el régimen supercrítico, dejan de existir dos fases distintas y existe apenas un fluido homogéneo.

Cerca del punto crítico, la materia fluctúa sin límites. Burbujas y gotas, unas tan pequeñas como unos cuantos átomos, otras tan grandes como el recipiente, aparecen y desaparecen, se unen y se separan. Exactamente en el punto crítico la escala de las mayores fluctuaciones divergen, pero el efecto de las fluctuaciones en escalas menores no es despreciable. La distribución de las fluctuaciones es invariable para transformaciones de escala.

De la figura se deduce que la teoría tiene una “simetría interna”: la figura no cambia cuando hacemos rotaciones en el plano definido por A y B. La invariancia es definida matemáticamente por transformaciones que dejan magnitudes sin cambio. Por ejemplo, la distancia entre dos puntos de un sólido que se mueve, pero no se deforma.
Simetrías locales y globales
Una simetría global es una simetría que sostiene todos los puntos en el tiempo-espacio bajo consideración, a diferencia de la simetría local que solo sostiene a un subconjunto de puntos.
La mayoría de las teorías físicas son descritas por lagrangianos (En física, un lagrangiano es una función matemática a partir del cual se pueden derivar la evolución temporal, las leyes de conservación y otras propiedades importantes de un sistema físico) que son invariantes bajo ciertas transformaciones, cuando las transformaciones son realizadas en diferentes puntos del espacio-tiempo y están relacionadas linealmente – ellas tienen simetría global.
Por ejemplo, en toda teoría cuántica la fase global de una función de onda es arbitraria y no representa algo físico. Consecuentemente, la teoría es invariante bajo a cambio global de fases (Agregando una constante a la fase de todas las funciones de onda, en todos lados); esto es una simetría global. En la electrodinámica quántica, la teoría es también invariante bajo un cambio local de fase, es decir, que se puede alterar la fase de todas las funciones de onda tal que la alteración sea diferente en cada punto del espacio-tiempo. Esto es una simetría local.

También se habla de ruptura de simetrías temporales en la física de partículas.
Los físicos creen también que están en el camino correcto porque, de algún modo que no pueden explicar, tienen la convicción de que son correctas, y las ideas de simetría son esenciales para esa intuición. Se presiente que es correcto que ningún lugar del Universo es especial comparado con cualquier otro lugar del Universo, así que los físicos tienen la confianza de que la simetría de traslación debería estar las simetrías de las leyes de la Naturaleza. Se presiente que es correcto que ningún movimiento a velocidad constante es especial comparado con cualquier otro. De modo que los físicos tienen confianza en que la relatividad especial, al abrazar plenamente la simetría entre todos los observadores con velocidad constante, es una parte esencial de las leyes de la Naturaleza.
La fórmula de Euler ilustrada en el plano complejo.
Se dice que esta ecuación de Euler es la más bella conocida. Aunque son muchas las ecuaciones que podríamos traer aquí y que son de todos conocidas y han quedado como símbolos en la historia de las matemáticas, la de Euler, es posible que por su elegancia y simplicidad, le pueda ganar a las demás en belleza. Ahí, en ese sencillo conjunto, los números más significativos de las matemáticas se abrazan: o, 1, e, π, y la unidad imaginaria i .
Si se fijan en la fórmula, en ella aparecen los 5 números más importantes en la historia de las matemáticas. El 0 y el 1 que, entre otras aportaciones a esta disciplina, son famosos por ser elementos neutros y, por lo tanto, indispensables en las operaciones de suma y producto; los números π y e, posiblemente, los dos irracionales más famosos (junto con φ, la razón aúrea) que existen (y que nos permiten hacer el chiste aquel de que la parte más irracional de nuestro cuerpo es el pi-e); y la unidad imaginaria, i, cuyo valor es
Dirac nos hablaba de ecuaciones bellas. La estética es, evidentemente, subjetiva, y la afirmación de que los físicos buscan la belleza en sus teorías tiene sentido sólo si podemos definir la belleza. Afortunadamente, esto se puede , en cierta medida, pues la estética científica está iluminada por el sol central de la simetría.
La Naturaleza nos la muestra por todas partes
La simetría es un concepto venerable y en modo alguno inescrutable y no podemos negar que tiene muchas implicaciones en la Ciencia, en las Artes y sobre todo, ¡en la Naturaleza! que de manera constante nos habla de ella. Miremos donde miremos…¡allí está!
El físico chino-norteamericano Chen Ning Yang ganó el Nóbel de Física por su en el desarrollo de una teoría de campos basada en la simetría y, aún afirmaba: “No comprendemos todavía el alcance del concepto de simetría”. Es lógico pensar que, si la Naturaleza emplea la simetría en sus obras, la razón debe estar implicada con la eficacia de los sistemas simétricos.
En griego, la palabra simetría significa “la misma medida” (syn significa “juntos”, como en sinfonía, una unión de sonidos, y metrón, “medición”); así su etimología nos informa que la simetría supone la repetición de una cantidad medible. Pero la simetría los griegos, también significaba la “la debida proporción”, lo que implicaba que la repetición involucrada debía ser armoniosa y placentera, como de hecho, resultan ser en las imágenes que arriba contemplamos. Asi, la Naturaleza nos está indicando que una relación simétrica debe ser juzgada por un criterio estético superior.

Simetría en la Naturaleza
Muchos de nosotros, la mayoría, conocimos la simetría en sus manifestaciones geométricas de aquellas primeras clases en la Escuela Elemental, más tarde en el arte y, finalmente, la pudimos percibir en la Naturaleza, en el Universo y en nosotros mismos que, de alguna manera, somos de ese Universo de simetría.
Los planetas son esféricos y, por ejemplo, tienen simetría de rotación. Lo que quiere indicar es que poseen una característica -en caso, su perfil circular- que permanece invariante en la transformación producida cuando la Natuiraleza los hace rotar. Las esferas pueden Hacerse rotar en cualquier eje y en cualquier grado sin que cambie su perfil, lo cual hace que sea más simétrica.

La clave de la belleza está en la simetría
La simetría por rotación se encuentra en los pétalos de una flor o en los tentáculos de una medusa: aunque sus cuerpos roten, permanecen iguales. La simetría bilateral que hace que los lados derecho e izquierdo sean iguales y se presenta en casi todos los animales, incluido nosotros. Pero es uniendo estos aspectos se obtienen figuras realmente armoniosas. Si se trata de desplazamiento y rotación en un mismo plano hablamos de una espiral, mientras que en el espacio sería una hélice, aunque ambas se encuentran por todas partes en la naturaleza.
Las simetrías se generan mediante las fuerzas que actúan sobre los cuerpos, descritas por leyes rigurosas e inequívocas, como una fórmula matemática y dependen de la existencia de fuerzas distintas que actúan en diversas direcciones. Si éstas permanecen en equilibrio, no hay preferencia alguna hacia arriba o abajo, a la derecha o a la izquierda, y los cuerpos tenderán a ser perfectamente esféricos, como suele ocurrir en el caso de virus y bacterias, las estrellas y los mundos… las galaxias. Además, cuando el aspecto no es el de una esfera perfecta, la Naturaleza hará todo lo posible para acercarse a esta .

La simetría también están presentes en nuestros cerebros, donde se repiten secuencias en muchas partes que lo conforman de las neuronas sin fin (cien mil millones como estrellas en la Galaxia).
¿Sería posible que la simetría material tuviera un paralelismo en la abstracción intelectual que son las leyes físicas? luego hace falta un esfuerzo mental considerable para pasar de lo material a lo intelectual, pero cuando se profundiza en ella, la conexión aparece. En la naturaleza existen muchas cosas que nos pueden llevar a pensar en lo complejo que puede llegar a resultar entender cosas que, a primera vista, parecían sencillas.
Me explico:

Sucesión Aurea es también su nombre. La relación entre la distancia entre las espiras del interior de cualquier caracol (no sólo del nautilus). Fijémonos, por ejemplo, en una Flor de Girasol y en las matemáticas que sus semillas conllevan. Forman una serie de números en la que cifra es la suma de las dos precedentes (por ejemplo 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…) se denomina, en términos matemáticos, sucesión de Fibonacci, una ley que se cumple incluso en el mundo vegetal, como hemos podido comprobar en las semillas del girasol, dispuestas en espiral y que respetan ésta fórmula. La podemos ver por todas partes.
Lo mismo ocurre con otros ejemplares de la diversidad del mundo de las plantas
En el mundo inorgánico las leyes de la cristalización del agua congelada, determinadas por las fuerzas que actúan entre las moléculas, hacen que los cristales adopten formas que son infinitas y varían con respecto a un tema común: la estrella de seis puntas. Sin embargo, los planetas son esféricos porque han nacido en la primordial que rodeaba al Sol, atrayendo materia indiferentemente de todas partes.
Extrañas creaciones de la Naturaleza
Claro que, en la Naturaleza, nada ocurre porque sí, todo tiene su por qué, y, todo lo que en ella podemos contemplar posee una funcionalidad que está directamente relacionada con su mecánica, con el medio en el que habita, con lo que el Universo espera que haga en su medio y, para ello, dota a figura con aquellos “trajes” que mejor les permita realizar aquello para lo que están destinados.
La salida del Sol se produce cada día, la formación del Agujero Negro sólo cuando la estrella masiva agosta su combustible nuclear de fusión, implosiona, se produce una Supernova, y, lo que queda es una Nebulosa y un temible agujero negro.
Vamos a generalizar un paso más el concepto de simetría, planteándonos si es posible que una ley física se cumpla en cualquier lugar. ¿En cualquier lugar… de dónde?, ¿de nuestra ciudad?, ¿de nuestro planeta? No: del universo. Una ley que fuera válida en cualquier lugar del universo sería una ley simétrica respecto al espacio. Se cumpliría dondequiera que se hiciese un experimento para comprobarla.
Fíjense que nuestra idea de simetría se va haciendo más compleja y más profunda. no nos detenemos en ver si la forma material de un objeto es simétrica, ni de si la escritura de una fórmula matemática es simétrica. Ahora nos preguntamos si una ley física es válida en todo el Universo.
La otra simetría interesante para una ley física es la que se refiere al tiempo. Cierta ley física se cumple ; ¿antes también?, ¿se cumplirá pasado algún tiempo? Una ley que fuera cierta en cualquier instante de la historia del universo sería una ley simétrica respecto al tiempo.

Lo que nos preguntamos es: ¿son simétricas o no las leyes de la física?
Todo lo que ocurre en la Naturaleza tiene su explicación
Hasta donde alcanzan nuestras medidas, las leyes físicas (y, por tanto, la interacción gravitatoria) sí son simétricas respecto al espacio y respecto al tiempo. En cualquier lugar y momento temporal del universo, la Naturaleza se comporta igual que aquí y ahora en lo que se refiere a estas leyes.
Esta simetría es un arma muy poderosa para investigar hacia el pasado y hacia el futuro, ya que nos permite suponer (y, en la medida en que confiemos en la seguridad de la simetría,conocer) locales donde jamás podremos llegar por la distancia espacial y temporal que nos separa de muchas partes del universo. Así, por ejemplo, gracias a esta simetría, podemos calcular que el Sol lleva 5.000 millones de años produciendo energía y que le quedan, probablemente, otros 5.000 millones hasta que consuma toda su masa. Esto lo podemos aventurar suponiendo que en ese enorme tramo de 5.000 + 5.000 = 10.000 millones de años las leyes físicas que determinan los procesos mediante los cuales el Sol consume su propia masa como combustible (las reacciones nucleares que le permiten producir energía), fueron, son y serán las mismas aquí en el Brazo de orión donde nos encontramos como en los arrabales de la Galaxia Andrómeda donde luce una estrella como nuestro Sol que, también envía luz y calor a sus planetas circundantes, y, por muy lejos que podamos mirar, siempre veremos lo mismo.

Por tanto, en cierto modo, la simetría se vuelve tan importante o más que la propia ley física.
La regularidad de las formas de la Naturaleza se refleja incluso en la cultura humana, que desde siempre intenta inspirarse en el mundo natural conformar su propio mundo. Existen hélices en las escaleras de palacios, castillos y minaretes y en las decoraciones de esculturas y columnas. Las espirales abundan en los vasos, en los bajorrelieves, en los cuadros, en las esculturas en los collares egipcios, griegos, celtas, precolombinos e hindúes e, incluso, en los tatuajes con los que los maoríes neozelandeses se decoran el rostro.

La búsqueda de la perfección geométrica y de las propiedades matemáticas pueden ser una guía importante en el estudio científico del mundo. Paul Dirac, una de los padres de la moderna mecánica cuántica, solía decir que “si una teoría es bella desde el punto de vista matemático, muy probablemente es también verdadera”.

En la Naturaleza, además de las simetrías, encontramos que, la Entropía, hace estragos. Arriba el irreversible cambio con el paso del Tiempo.
A todo esto, no debemos olvidar que todo, sin excepción, en nuestro Universo, está sometido a la Entropía que nos trae el paso inexorable de eso que llamamos “Tiempo”, y que, convierte perfectas simetrias de joven belleza, en deteriorados objetos o entidades que, nos viene a recordar que nada es perpetuo, que todo pasa y se transforma. Claro que, de alguna manera, todo vuelve a resurgir. Pero, si somos consciente de lo efímera que es la belleza… ¡Seremos más humildes y menos vanidosos!
La convivencia puede darnos el amor más profundo, o, el más profundo odio
Un dolor que llevo dentro de mí es el no poder contemplar la verdadera belleza que estando presente en los seres vivos inteligentes, en la mayoría de los casos, se nos queda oculta a nuestra percepción, toda vez que esa clase de belleza, que no podemos ver pero sí percibir, sólo la podemos captar con el trato y la convivencia y, verdaderamente, tengo que admitir que, algunas bellezas que he tenido la suerte de poder “ver con los ojos del espíritu”, llegan a ser segadoras, deslumbrantes, su esplendor es muy superior al de la estrella más brillante del cielo, y, seguramente (estoy seguro) como a muchos de ustedes les pasa, tengo la suerte de tenerla junto a mí desde hace muchos años. y, si pienso en ello en profundidad y detenimiento, no tengo más remedio que concluir que es ese brillo y esplendor el que me da la fuerza para seguir cada dia en la dura lucha que nos ha participar.
¡Sí que es importante la Belleza! Dirac tenía toda la razón. Y, no digamos la Simetría que indican con el dedo de la Naturaleza el camino a seguir a muchos físicos que quieren desvelar sus secretos.
emilio silvera
Mar
25
¿Una guía para descubrir? ¡La simetría!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Simetrías ~
Clasificado en Simetrías ~
 Comments (0)
Comments (0)
La simetría esférica del planeta Marte vista por el Hubble
Esta figura se puede dividir de una forma, verticalmente. Si la intentamos dividir horizontalmente, los dos lados no coincidirían. Dividida de esta forma, la mitad superior no coincide con la mitad inferior. Por lo tanto, podemos decir que la mariposa tiene simetría bilateral .
La simetría es una propiedad universal tanto en la vida corriente, un punto de vista matemático como desde el quehacer de la Física Teórica. En realidad, lo que observamos en la vida corriente es siempre lo repetitivo, lo simétrico, lo que se puede relacionar entre sí por tener algo común.
La Naturaleza está llena de simetrías
En un sentido dinámico, la simetría podemos entenderla como lo que se repite, lo reiterativo, lo que tiende a ser igual. Es decir, los objetos que, por mantener la misma geometría, son representativos de otros objetos. En el Caos matemático encontramos concepción de la simetría en el mundo los fractales. Sin embargo, la simetría es mucho más.
Cuando miro en mi diccionario de Física la palabra Simetría, lo que me dice es:
“Conjunto de invariancias de un sistema. Al aplicar una transformación de simetría sobre un sistema, el sistema queda inalterado, la simetría es estudiada matemáticamente usando teoría de grupos. Algunas de las simetrías son directamente físicas. Algunos ejemplos son las reflexiones y las rotaciones en las moléculas y las translaciones en las redes cristalinas. Las simetrías pueden ser discretas (es decir, cuando hay un finito de transformaciones de simetría), como el conjunto de rotaciones de una molécula octaédrica, o continuas (es decir, cuando no hay número finito), como el conjunto de rotaciones de un átomo o núcleo. Existen simetrías más generales y abstractas, como la invariancia CTP y las simetrías asociadas a las teorías gauge.”
Estas moléculas esféricas de carbono, conocidas como buckybolas, se agitan, como si estuvieran hechas de gelatina. Las buckybolas son moléculas con forma de balón de fútbol…

El Universo está lleno de simetrías por todas partes
También podemos hablar de simetría rota y de supersimetrías. Durante los últimos tiempos, los Físicos han elevado los principios de simetría al más alto nivel en la escala de lo que podemos entender por una explicación. Cuando encontramos una Ley propuesta de la Naturaleza, una pregunta se nos viene a la mente: ¿Por qué ley? ¿Por qué la relatividad especial y la general? ¿Por qué el electromagnetismo de Maxwell? ¿Por qué las teorías de Yang-Mills de las fuerzas nucleares fuerte y débil? Claro que, una respuesta de importancia es que, las teorías hacen predicciones que han sido repetidamente conformadas con precisos experimentos, con diversidad de científicos y lugares y que, siempre, en todos los casos, dieron el mismo resultado. Esto, por supuesto, es la base de la confianza esencial que los físicos tienen en esas teorías.
En todos estos fantásticos lugares rigen las mismas leyes
Claro que, se deja fuera algo esencial: Los físicos creen también que están en el camino correcto porque, de algún modo que no pueden explicar, tienen la convicción de que son correctas, y las ideas de simetría son esenciales para esa intuición. Se presiente que es correcto que ningún lugar del Universo es especial comparado con cualquier otro lugar del Universo, así que los físicos tienen la confianza de que la simetría de traslación debería estar las simetrías de las leyes de la Naturaleza. Se presiente que es correcto que ningún movimiento a velocidad constante es especial comparado con cualquier otro. De modo que los físicos tienen confianza en que la relatividad especial, al abrazar plenamente la simetría todos los observadores con velocidad constante, es una parte esencial de las leyes de la Naturaleza.
Los hongos atómicos guardan cierta simetría
Así que las simetrías de la Naturaleza no son meras consecuencias de las leyes de la Naturaleza. Desde nuestra perspectiva moderna, las simetrías son la base de la que manan las leyes y, siendo así (que lo es), cuando un físico observa una simetría, agudiza su atención, ya que, allí, en aquel lugar, podría encontrarse alguna ley de la Naturaleza que siguiendo aquella presencia, se podría .
Más allá de su papel en dar forma a las leyes que gobiernan las fuerzas de la Naturaleza, las ideas de simetría son vitales para el propio concepto del tiempo. Nadie ha sabido encontrar todavía definición fundamental y definitiva del tiempo. Sin embargo, es indudable que el papel del tiempo en la constitución del cosmos es llevar una especie de de los sucesos y acontecimientos que en el universo ocureren: Nace una estrella, se forma una nueva galaxia, explota una supernova, muere una estrella masiva y surge un agujero negro…

Sí, todos fuimos jóvenes y el paso del tiempo nos transformó en más viejos , no por ello más sabios. Eso sí, con algo más de experiencia y más prudentes a la hora de decidir sobre las cosas importantes que siempre, aunque de joven no le prestemos atención, traen consecuencias.
Sí, todo cambia y nada permanece con el inexorable paso del Tiempo
Reconocemos el transcurrir del tiempo al mirar y ver que, las cosas, no son iguales hoy que lo fueron ayer. Con el transcurrir del tiempo todo cambia y nada permanece. ¿Será el tiempo otra simetría? Debe serlo, ya que, ningún cambio le afecta y, su transcurrir queda inalterado por mucho camino que pudiera haber recorrido y, eso, lo diferente de todo lo demás: Todo cambia excepto el tiempo.
Así, tenemos que llegar a la conclusión de que, el concepto de simetría es, para los Físicos, indispensable como punto de referencia en el descubrimiento de las teorías que más tarde, llegan a convertirse en leyes de la Naturaleza al comprobarse que, son inalterables: Otra vez la Simetría. El desarrollo de la moderna teoría cosmológica, por ejemplo, tiene mucho que ver con la simetría. El significado del Tiempo, su aplicabilidad al universo en su conjunto, la global del espacio, e incluso el marco subyacente de la relatividad especial, todo descansa sobre fundamentos de simetría.
Hay simetría en la muy grande y, también, en lo muy pequeño
Durante el último siglo un concepto muy importante en Física, sobre todo en Mecánica Cuántica, ha sido y es el de simetría. Uno de los resultados más bonitos de la Física dice que allá donde hay una simetría hay una cantidad conservada.
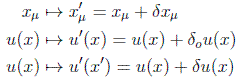
El teorema de Noether se expresa en primer orden como:
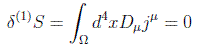
“Teorema (Noether). A toda transformación continua de las coordenadas o/y los campos que deje invariante la acción en un volumen cuadridimensional le corresponde una corriente conservada jμ en la evolución que cumple Dμjμ=0.”
Es lo que se llama teorema de Noether. De este modo, las leyes de la Física pueden ser iguales bajo una u otra simetría y cada uno de esos casos se conservará algo. Así por ejemplo, la simetría de traslación temporal corresponde a una cantidad conservada: la energía. También ocurre que las leyes de la física son las mismas bajo unas transformaciones de rotación en el espacio tridimensional y eso significa que se conserva el momento angular.
Allí donde veamos presente la simetría, debemos prestar atención, ya que, podría ser el indicio de que algo importante se podría derivar de esa simetría presente que, en física, hemos comentado, es un principio de gran importancia.


Jun
25
¿Una guía para descubrir? ¡La simetría!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Simetrías ~
Clasificado en Simetrías ~
 Comments (1)
Comments (1)

La simetría esférica del planeta Marte
La simetría es una propiedad universal tanto en la vida corriente, desde un punto de vista matemático como desde el quehacer de la Física Teórica. En realidad, lo que observamos en la vida corriente es siempre lo repetitivo, lo simétrico, lo que se puede relacionar entre sí por tener algo común.
En un sentido dinámico, la simetría podemos entenderla como lo que se repite, lo reiterativo, lo que tiende a ser igual. Es decir, los objetos que, por mantener la misma geometría, son representativos de otros objetos. En el Caos matemático encontramos esta concepción de la simetría en el mundo los fractales. Sin embargo, la simetría es mucho más.
Cuando miro en mi diccionario de Física la palabra Simetría, lo que me dice es: “Conjunto de invariancias de un sistema. Al aplicar una transformación de simetría sobre un sistema, el sistema queda inalterado, la simetría es estudiada matemáticamente usando teoría de grupos. Algunas de las simetrías son directamente físicas. Algunos ejemplos son las reflexiones y las rotaciones en las moléculas y las translaciones en las redes cristalinas. Las simetrías pueden ser discretas (es decir, cuando hay un número finito de transformaciones de simetría), como el conjunto de rotaciones de una molécula octaédrica, o continuas (es decir, cuando no hay número finito), como el conjunto de rotaciones de un átomo o núcleo. Existen simetrías más generales y abstractas, como la invariancia CTP y las simetrías asociadas a las teorías gauge.”

El Universo está lleno de simetrías por todas partes
También podemos hablar de simetría rota y de supersimetrías. Durante los últimos tiempos, los Físicos han elevado los principios de simetría al más alto nivel en la escala de lo que podemos entender por una explicación. Cuando encontramos una Ley propuesta de la Naturaleza, una pregunta se nos viene a la mente: ¿por qué esta ley? ¿Por qué la relatividad especial y la general? ¿Por qué el electromagnetismo de Maxwell? ¿Por qué las teorías de Yang-Mills de las fuerzas nucleares fuerte y débil? Claro que, una respuesta de importancia es que, las teorías hacen predicciones que han sido repetidamente conformadas con precisos experimentos, con diversidad de científicos y lugares y que, siempre, en todos los casos, dieron el mismo resultado. Esto, por supuesto, es la base de la confianza esencial que los físicos tienen en esas teorías.
Constelaciones
Claro que, se deja fuera algo esencial: Los físicos creen también que están en el camino correcto porque, de algún modo que no pueden explicar, tienen la convicción de que son correctas, y las ideas de simetría son esenciales para esa intuición. Se presiente que es correcto que ningún lugar del Universo es especial comparado con cualquier otro lugar del Universo, así que los físicos tienen la confianza de que la simetría de traslación debería estar entre las simetrías de las leyes de la Naturaleza. Se presiente que es correcto que ningún movimiento a velocidad constante es especial comparado con cualquier otro. De modo que los físicos tienen confianza en que la relatividad especial, al abrazar plenamente la simetría entre todos los observadores con velocidad constante, es una parte esencial de las leyes de la Naturaleza.
Los hongos atómicos también guardan cierta simetría
Así que las simetrías de la Naturaleza no son meras consecuencias de las leyes de la Naturaleza. Desde nuestra perspectiva moderna, las simetrías son la base de la que manan las leyes y, siendo así (que lo es), cuando un físico observa una simetría, agudiza su atención, ya que, allí, en aquel lugar, podría encontrarse alguna ley de la Naturaleza que siguiendo aquella presencia, se podría descubrir.

Más allá de su papel en dar forma a las leyes que gobiernan las fuerzas de la Naturaleza, las ideas de simetría son vitales para el propio concepto del tiempo. Nadie ha sabido encontrar todavía definición fundamental y definitiva del tiempo. Sin embargo, es indudable que el papel del tiempo en la constitución del cosmos es llevar una especie de registro de los sucesos y acontecimientos que en el universo ocureren: Nace una estrella, se forma una nueva galaxia, explota una supernova, muere una estrella masiva y surge un agujero negro…

Sí, todos fuímos jóvenes y el paso del tiempo nos transformó en más viejos pero, no por ello más sabios. Eso sí, con algo más de experiencia y más prudentes a la hora de decidir sobre las cosas importantes que siempre, aunque de joven no le prestemos atención, trae consecuencias.
Reconocemos el transcurrir del tiempo al mirar y ver que, las cosas, no son iguales hoy que lo fueron ayer. Con el transcurrir del tiempo todo cambia y nada permanece. ¿Será el tiempo otra simetría? Debe serlo, ya que, ningún cambio le afecta y, su transcrrir queda inalterado por mucho camino que pudiera haber recorrido y, eso, lo hace diferente de todo lo demás: Todo cambia excepto el tiempo.
Así, tenemos que llegar a la conclusión de que, el concepto de simetría es, para los Físicos, indispensable como punto de referencia en el descubrimiento de las teorías que más tarde, llegan a convertirse en leyes de la Naturaleza al comprobarse que, son inalterables: Otra vez la Simetría. El desarrollo de la moderna teoría cosmológica, por ejemplo, tiene mucho que ver con la simetría. El signioficado del Tiempo, su aplicabilidad al universo en su conjunto, la forma global del espacio, e incluso el marco subyacente de la relatividad especial, todo descansa sobre fundamentos de simetría.
Durante el último siglo un concepto muy importante en Física, sobre todo en Mecánica Cuántica, ha sido y es el de simetría. Uno de los resultados más bonitos de la Física dice que allá donde hay una simetría hay una cantidad conservada. Es lo que se llama teorema de Noether. De este modo, las leyes de la Física pueden ser iguales bajo una u otra simetría y para cada uno de esos casos se conservará algo. Así por ejemplo, la simetría de traslación temporal corresponde a una cantidad conservada: la energía. También ocurre que las leyes de la física son las mismas bajo unas transformaciones de rotación en el espacio tridimensional y eso significa que se conserva el momento angular.
Allí donde veamos presente la simetría, debemos prestar atención, ya que, podría ser el indicio de que algo importante se podría derivar de esa simetría presente que, en física, como hemos comentado, es un principio de gran importancia.

















 Totales: 74.828.798
Totales: 74.828.798 Conectados: 30
Conectados: 30












































