Nov
22
¡Las Galaxias! ¡La Entropía! ¡El Universo! ¡La Vida!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Astronomía y Astrofísica ~
Clasificado en Astronomía y Astrofísica ~
 Comments (0)
Comments (0)
Vía Láctea (como otras galaxias espirales) es una zona de reducción de entropía…, así se deduce de varios estudios realizados y se puede argumentar que, las galaxias deben ser consideradas, por su dinámica muy especial, como sistemas vivos. En planteamiento más prudente se señala que el test de Lovelock constituye lo que se llama una condición “necesaria, pero no suficiente” para la existencia de vida. Si un sistema se encuentra en equilibrio termodinámico -si no supera el test de Lovelock-, podemos tener la seguridad de que está muerto. Si está vivo, debe producir una reducción de la entropía y superar dicho test.

Pero un sistema podría producir entropía negativa sin estar vivo, como en el caso de contracción por efecto de la gravedad que hemos comentado a lo largo de estos trabajos. Desde este punto de vista, no hay frontera claramente definida entre los objetos vivos y la materia “inerte”. Yo, por mi parte creo que, la materia nunca es inerte y, en cada momento, simplemente ocupa la fase que le ha tocado representar en ese punto del espacio y del tiempo.

James y Sandy Lovelock ¿Qué haríamos sin ellas?
El mero hecho de que la frontera entre la vida y la ausencia de vida sea difuso, y que el lugar en el que haya que trazar la línea sea un tema de discusión, es, sin embargo, un descubrimiento importante. Contribuye a dejar claro que en relación con la vida no hay nada insólito en el contexto del modo en que funciona el Universo.
Como ya hemos visto en las explicaciones de otros trabajos expuestos aquí, es natural que los sistemas simples se organicen en redes al borde del caos y, una vez que lo hacen, es natural que la vida surja allí donde hay “una pequeña charca caliente” que sea adecuada para ello. Esto es parte de un proceso más o menos continuo, sin que haya un salto repentino en el que comience la vida. Desde ese punto de vista, lo más importante que la ciencia podría lograr sería el descubrimiento de, al menos, otro planeta en el que haya surgido la vida.

Gracias a la teoría de Lovelock sobre la naturaleza de la vida estamos a punto de poder conseguirlo, y es posible que antes de los próximos 50 años se lance al espacio un telescopio capaz de encontrar planetas con sistemas como el de Gaia, nuestra Tierra.
Hay dos etapas del descubrimiento de estas otras Gaias. En primer lugar debemos ser capaces de detectar otros planetas del tamaño de la Tierra que describan órbitas alrededor de otras estrellas; luego tenemos que analizar la atmósfera de esos planetas para buscar pruebas de que los procesos de reducción de la entropía están en marcha. Los primeros planetas “extrasolares” se detectaron utilizando técnicas Doppler, que ponían de manifiesto unos cambios pequeñísimos en el movimiento de las estrellas alrededor de las cuales orbitaban dichos planetas. Este efecto, que lleva el nombre del físico del siglo XIX Christian Doppler, modifica la posición de las líneas en el espectro de la luz de un objeto, desplazándolas en una cantidad que depende de lo rápido que el objeto se mueva con respecto al observador.

Zonas habitables, los astrónomos han ignorado las enanas blancas en su búsqueda de exoplanetas. Esto puede haber sido un error, de acuerdo con un nuevo estudio de zonas habitables en enanas blancas. Aunque los agujeros negrosy las estrellas de neutrones captan toda la atención como destinos finales de las estrellas, la mayor parte nunca llegarán a ese extremo. Aproximadamente el 97 por ciento de las estrellas de nuestra galaxia no son lo bastante masivas para acabar en ninguna de esas dos opciones.
En lugar de eso, los astrónomos creen que terminarán sus vidas como enanas blancas, densos y calientes trozos de materia inerte en los que las reacciones nucleares terminaron hace mucho. Estas estrellas tienen aproximadamente el tamaño de la Tierra y se mantienen en contra del colapso gravitatorio mediante el Principio de Exclusión de pauli, el cual evita que los electrones ocupen el mismo estado al mismo tiempo. Pero, a todo esto, hay que pensar en el tirón gravitatoria que una de estas estrellas podría incidir sobre cualquier planeta.
Para hacernos una idea de lo que es este tipo de observaciones, pensemos que el tirón gravitatorio que Júpiter ejerce sobre el Sol produce en éste un cambio de velocidad de unos 12,5 metros por segundo, y lo desplaza (con respecto al centro de masa del Sistema solar) a una distancia de 800.000 kilómetros, más de la mitad del diámetro de este astro, cuando el Sol y Júpiter orbitan en torno a sus recíprocos centros de masa. La velocidad de este movimiento es comparable a la de un corredor olímpico de 100 metros lisos y, para un observador situado fuera del Sistema solar, esto, por el efecto Doppler, produce un pequeñísimo desplazamiento de vaiven en la posición exacta de las líneas del espectro de luz emitida por el Sol.
Se trata del tipo de desplazamiento que se ha detectado en la luz a partir de los datos de algunas estrellas de nuestro entorno, y demuestra que en torno a ellas orbitan cuerpos celestes similares a Júpiter. Como ilustración diremos que la Tïerra induce en el Sol, mientras orbita alrededor de él, un cambio de velocidad de tan sólo 1 metro por segundo (la velocidad de un agradable paseo), y desplaza al Sol únicamente 450 kilómetros, con respecto al centro de masa del Sistema solar. No se dispone aún de la tecnología necesaria para medir un efecto tan pequeño a distancias tales como las de nuestras estrellas, y, pensemos que, la más cercana (Alfa Centauri), está situada a 4,3 a.l. de la Tierra, esta es la razón por la cual no se han detectado aún planetas similares a la Tierra.

Sistema Alfa Centauri
Hay otras técnicas que podrían servir para identificar planetas más pequeños. Si el planeta pasa directamente por delante de su estrella (una ocultación o un tránsito), se produce un empalidecimiento regular de la luz procedente de dicha estrella. Según las estadísticas, dado que las órbitas de los planetas extrasolares podrían estar inclinadas en cualquier dirección con respecto a nuestra posición, sólo el 1 por ciento de estos planetas estará en órbitas tales que podríamos ver ocultaciones y, en cualquier caso, cada tránsito dura sólo unas pocas horas (una vez al año para un planeta que tenga una órbita como la de la Tierra; una vez cada once años para uno cuya órbita sea como la de Júpiter.

El universo observable tiene un diámetro de aproximadamente 93 mil millones de años luz. Las distancias dentro del Sistema Solar se miden en unidades astronómicas (UA), donde 1 UA es la distancia media entre la Tierra y el Sol, alrededor de 150 millones de kilómetros. Para distancias más grandes fuera del Sistema Solar, se utiliza el año luz, que es la distancia que recorre la luz en un año, y es equivalente a unos 9,46 billones de kilómetros.
Cuando los humanos miramos al espacio y pensamos en sus increíbles distancias, es inevitable imaginar que sería posible encontrar algún sitio como nuestra casa. No sería lógico creer que sólo en la Tierra se han dado las condiciones para la vida. En nuestra misma Galaxia, planetas como la Tierra los hay a miles o cientos de miles.

Existen, sin embargo, proyectos que mediante el sistema de lanzar satélites al espacio que controlaran el movimiento (cada uno de ellos) de un gran número de estrellas con el fin de buscar esas ocultaciones. Si se estudian 100.000 estrellas, y 1.000 de ellas muestran tránsitos, la estadística resultante implicaría que prácticamente
toda estrella similar al Sol está acompañada por planetas. Sin embargo, aunque todas las búsquedas de este tipo son de un valor inestimable, la técnica Doppler es la que, de momento, se puede aplicar de manera más general a la búsqueda de planetas similares a la Tierra. De cualquier manera, independientemente de los planetas de este tipo que se descubran, lo que está claro es que, de momento, carecemos de la tecnología necesaria para dicha búsqueda.


La mejor perspectiva que tenemos en el momento inmediato, es la que nos ofrece el satélite de la NASA llamado SIM (Space Interforometry Mission) que mediante la técnica de interferometría (combinar los datos de varios telescopios pequeños para imitar la capacidad de observación de un telescopio mucho mayor) ver y medir la posición de las estrellas con la exactitud necesaria para descubrir las oscilaciones que delaten la presencvia de planetas como la Tierra que describen orbitas alrededor de cualquiera de las 200 estrellas más cercanas al Sol, así como por cualquiera de los planetas similares a Júpiter hasta una distancia del Sol que podría llegar hasta los 3.000 años luz.
Hacia el final de la década presente (si todo va bien), la Agencia Espacial Europea lanzará un satélite cuyo nombre será GAIA y que tendrá como misión principal, no precisamente buscar otras Gaias, sino trazar un mapa con las posiciones de los mil millones de objetos celestes más brillantes. Dado que GAIA tendrá que observar tantas estrellas, no mirará cada una muchas veces ni durante mucho tiempo, por lo que no podría detectar las oscilaciones ocasionadas por planetas similares a la Tierra; pero si podría detectar planetas del tamaño de Júpiter y, si estos planetas son tan abundantes como parece indicar los datos obtenidos hasta ahora, no es descabellado pensar que, puedan estar acompañados, como en nuestro propio Sistema solar, por otros planetas más pequeños.


Dentro de los próximos 10 años, deberíamos tener localizados decenas de miles de sistemas planetarios extrasolares en las zonas de la Vía Láctea próxima a nosotros. Sin embargo, seguiría tratándose de observaciones indirectas y, para captar los espectros de algunos de esos planetas, se necesita dar un salto más en nuestra actual tecnología que, como he dicho, resulta insuficiente para realizar ciertas investigaciones que requieren y exigen mucha más precisión.
Los nuevos proyectos y las nuevas generaciones de sofisticados aparatos de alta precisión y de IA avanzada, nos traerán, en los próximos 50 años, muchas alegrías y sorpresas que ahora, ni podemos imaginar.
Cambiemos de tema: ¿Qué es una partícula virtual?

Diagrama de Feynmann. No pocas veces hemos dicho que, en una partícula virtual las relaciones que normalmente existen entre las magnitudes físicas de cualquier partícula no tienen por qué cumplirse. En particular, nos interesan dos magnitudes, que seguro que conocéis de sobras: energía y momento.
Por partícula-antipartícula que aparece de la “nada” y luego se aniquila rápidamente sin liberar energía. Las partículas virtuales pueblan la totalidad del espacio en enormes cantidades, aunque no pueden ser observadas directamente.
En estos procesos no se viola el principio de conservación de la masa y la energía siempre que las partículas virtuales aparezcan y desaparezcan lo suficientemente rápido como para que el cambio de masa o energía no pueda ser detectado. No obstante, si los miembros de una partícula virtual se alejan demasiado como para volverse a juntar, pueden convertirse en partículas reales, según ocurre en la radiación Hawking de un agujero negro; la energía requerida para hacer a las partículas reales es extraída del agujero negro.

En el Gran Colisionador de Hadrones (LHC) a las 14:22 del día 23 de Noviembre del 2009, el detector ATLAS registro la primera colisión de protones en el LHC, seguido del detector CMS, y mas tarde los detectores ALICE y LHCb. Estas primeras colisiones solo son para probar la sincronización de las colisiones de haces de protones con cada uno de los detectores, lo cual resultó con éxito en cada uno de los experimentos y, marca un avance muy alentador hacia la tan esperada etapa (pasada en parte) de toma de datos donde se pueda buscar la partícula dadora de masas a las demás partículas, Super Simetría, Dimensiones Extras, y tantas otras cosas mas que surgen de la inmensa imaginación del intelecto humano.
Es sin duda un momento para recordar, especialmente para aquellos que han invertido parte de su vida en un proyecto tan grande e importante como este con la esperanza de alcanzar el conocimiento sobre la materia, la Naturaleza y el Universo mismo que, nunca pudimos soñar.
Pero, continuémos con la virtualidad de las partículas. La vida media de una partícula virtual aumenta a medida que disminuye la masa o energía involucrada. Así pues, un electrón y un positrón pueden existir durante unos 4×10-21 s, aunque un par de fotones de radio con longitud de onda de 300.000 km pueden vivir hasta un segundo.
En realidad, lo que llamamos espacio vacío, está rebosante de partículas virtuales que bullen en esa “nada” para surgir y desaparecer continuamente en millonésimas de segundo. ¡los misterios del Universo!

¿Qué es la Era de Planck? La Era de Planck es un período en la historia temprana del universo que se extiende desde el momento del Big Bang hasta aproximadamente 10–43 segundos después del evento inicial
En la teoría del Big Bang, fugaz periodo de tiempo entre el propio Big Bang y el llamado Tiempo de Planck, cuando el Universo tenía 10-43 segundo de edad y la temperatura era de 1034 k.
Durante este periodo, se piensa que los efectos de la Gravitación cuántica fueron dominantes. La comprensión teórica de esta fase es virtualmente inexistente.
Plasma.

El plasma forma las estrellas y otros objetos estelares que podemos ver, es la mayor concentración de materia del universos visible. Según algunos el cuarto estado de la materia que consiste en electrones y otras partículas subatómicas sin ninguna estructura de un orden superior a la de los núcleos atómicos.
Se trata de un Gas altamente ionizado en el que el número de electrones libres es aproximadamente igual al número de iones positivos. Como dije antes, a veces descrito como el cuarto estado de la materia, las plasmas aparecen en el espacio interestelar, en las atmósferas de las estrellas (incluyendo el Sol), en tubos de descarga y en reactores nucleares experimentales.

El plasma está bien presente en todos los remanentes de supernovas
Debido a que las partículas en un plasma están cargadas, su comportamiento difiere en algunos aspectos a un gas. Los plasmas pueden ser creados en un laboratorio calentando un gas a baja presión hasta que la energía cinética media de las partículas del gas sea comparable al potencial de ionización de los átomos o moléculas de gas. A muy altas temperaturas, del orden de 50.000 K en adelante, las colisiones entre las partículas del gas causan una ionización en cascada de este. Sin embargo, en algunos casos, como en lámparas fluorescentes, la temperatura permanece muy baja al estar las partículas del plasma continuamente colisionando con las paredes del recipiente, causando enfriamiento y recombinación. En esos casos la ionización es solo parcial y requiere un mayor aporte de energía.
En los reactores termonucleares, es posible mantener una enorme temperatura del plasma confinándolo lejos de las paredes del contenedor usando campos electromagnéticos.
El estudio de los plasmas se conoce como física de plasmas y, en el futuro, dará muy buenos beneficios utilizando en nuevas tecnologías como la nanotecnología que se nos viene encima y será el asombro del mundo.
Pluralidad de mundos.
Muchos mundos, como la Tierra, estarán situados en la zona habitable de sus estrellas y, el agua líquida, correra por los riachuelos y océanos. Si eso es así (que lo será), muchos mundos estarán habitados y, algún día lejano en el futuro, podremos saber de ellos con precisión antes de que se produzca el contacto.
Desde tiempos inmemoriales, grandes pensadores de los siglos pasados, dejaron constancia de sus pensamientos y creencia de que, allá arriba, en los cielos, otras estrellas contenían mundos con diversidad de vida, como en el planeta Tierra. Tales ideas, han acompañado al hombre que, no en pocas oportunidades, fueron tachados de locos.
Hoy, con los conocimientos que poseemos, lo que sería una locura es precisamente pensar lo contrario. ¡que estamos solos!
La Vía Láctea (una sola Galaxia de los cientos de miles de millones que pueblan el Universo), tiene más de 100.000 millones de estrellas. Miles de millones de Sistemas Solares. Cientos de miles de millones de planetas. Muchos miles y miles de estrellas como el Sol de tamaño mediano, amarillas de tipo G.
¿Cómo podemos pensar que solo el planeta Tierra alberga vida?
Protogalaxia.
Galaxia en proceso de formación. A pesar de la enorme técnica y sofisticación de los aparatos con que contamos para la observación del cosmos, no se ha podido encontrar ninguna proto-galaxia cercana, lo cual indica que todas o la mayoría de las galaxias se formaron hace mucho tiempo. Por otra parte, los científicos pensaban que no existía nada mas pequeño que un protón. En 1968 se descubrieron nuevas partículas dentro del protón, las cuales fueron llamadas quarks. Existen tres quarks dentro de cada protón, estos quarks se mantienen unidos entre sí mediante otras partículas llamadas gluones.
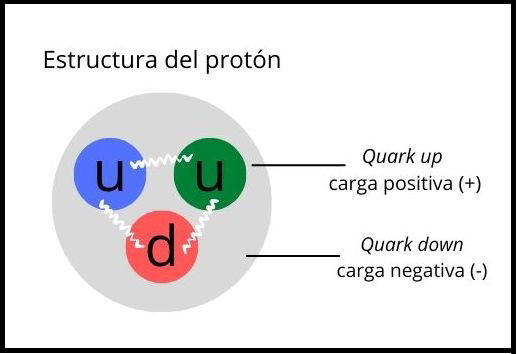
Partícula masiva del Grupo o familia de los Hadrones que se clasifica como Barión. Esta hecho por dos quarks up y un quark down y es, consecuentemente una partícula masiva con 938,3 MeV, algo menos que la del neutron. Su carga es positiva y su lugar está en el núcleo de los átomos, por lo que se les llama de manera genérica con los neutrones con la denominación de nucleones.

Este diagrama esquemático de un púlsar ilustra las líneas de campo magnético en blanco, el eje de rotación en verde y los dos chorros polares de radiación en azul. Un Pulsar es… Una fuente de radio desde la que se recibe un tren de pulsos altamente regular. Ha sido catalogado más de 600 púlsares desde que se descubriera el primero en 1.976. Los púlsares son estrellas de neutrones en rápida rotación, con un diámetro de 20-30 km. Las estrellas se hallan altamente magnetizadas (alrededor de 108 teslas), con el eje magnético inclinado con respecto, al eje de rotación. La emisión de radio se cree que surge por la aceleración de partículas cargadas por encima de los polos magnéticos. A medida que rota la estrella, un haz de ondas de radio barre la Tierra, siendo entonces observado el pulso, de forma similar a un faro.
Los periodos de los pulsos son típicamente de 1 s., pero varían desde los 1’56 ms (púlsares de milisegundo) hasta los cuatro con tres s. Estos periodos rotacionales van decreciendo a medida que la estrella pierde energía rotacional, aunque unos pocos púlsares jóvenes son propensos a súbitas perturbaciones conocidas como ráfagas.
Las medidas precisas de tiempos en los púlsares han revelado la existencia de púlsares binarios, y un púlsar, PSR 1257+12, se ha demostrado que está acompañado de objetos de masa planetaria. Han sido detectado objetos ópticos (destellos) procedentes de unos pocos púlsares, notablemente los púlsares del Cangrejo y Vela.
Se crean en explosiones de supernovas de estrellas supergigantes y otros a partir de enanas blancas, se piensa que puedan existir cien mil en la Vía Láctea.

Quasars
Objeto con un alto desplazamiento al rojo y con apariencia de estrella, aunque es probablemente el núcleo activo muy luminoso de una galaxia muy distante. El nombre es una contracción del ingles quasi stellar, debido a su apariencia estelar. Los primeros quasars descubiertos eran intensos fuentes de radio. Debido a las grandes distancias indicadas por el desplazamiento al rojo del núcleo debe ser hasta 100 veces más brillante que la totalidad de una galaxia normal. Además algunos quasars varían en brillo en una escala de tiempo de semanas, indicando que esta inmensa cantidad de energía se origina en un volumen de unas pocas semanas-luz de longitud. La fuente puede, por tanto, ser un disco de acreción alrededor de un agujero negro de 107 o 108 masas solares.

Imagen de 3C273 recogida por el telescopio Hubble
El primer quasar en ser identificado como tal en 1.963 fue la radiofuente 3c 273 con un desplazamiento al rojo de 0,158, siendo todavía el quasar más brillante, óptimamente hablando, observado desde la Tierra, con magnitud 13. Miles de quasar han sido descubiertos desde entonces. Algunos tienen desplazamiento al rojo tan grandes como 4,9, implicando que lo vemos tal como eran cuando el Universo tenía sólo una décima parte de la edad actual.
En esta brevísima reseña no puede dejarse constancia de todo lo que se sabe sobre quasars, sin embargo, dejamos los rasgos más sobresalientes para que el lector obtenga un conocimiento básico de estos objetos estelares. Para finalizar la reseña diré que, algunas galaxias aparentemente normales pueden contener remanentes de actividad quasar en sus núcleos, y algunas galaxias Seyfert y galaxias Markarian tienen núcleos que son intrínsecamente tan brillantes como algunos quasars. Existen algunas evidencias de que los quasars aparecen en los núcleos de los espirales, y es esa interacción con una galaxia vecina la que proporciona gas o estrellas al núcleo formado por un agujero negro masivo, alimentando así la emisión del quásar. Salvo mejor parecer.

La radiación cósmica de fondo es la luz residual que quedó de ese momento, y actualmente se presenta como un fondo de microondas en todas las direcciones del cielo. La radiación cósmica de fondo fue descubierta, en 1965, por los astrónomos Arno Penzias y Robert Wilson.
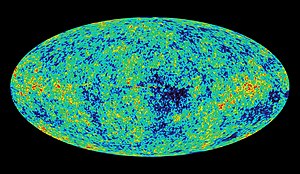
Radiación cósmica de fondo.
Antes, hemos comentado por alguna parte que, se trata de emisión radio de microondas proveniente de todas las direcciones (isotrópica) y que corresponde a una curva de cuerpo negro. Estas propiedades coinciden con las predichas por la teoría del Big Bang, como habiendo sido generada por fotones liberados del Big Bang cuando el Universo tenía menos de un millón de años (Universo bebé) de antigüedad.
La teoría del Big Bang también supone la existencia de radiaciones de fondo de neutrinos y gravitatoria, aunque aun no tenemos los medios para detectarlas. Sin embargo, los indicios nos confirman que la teoría puede llevar todas las papeletas para que le toque el premio.
Últimamente se ha detectado que la radiación cósmica de fondo no está repartida por igual por todo el Universo, sino que, al contrario de lo que se podía esperar, su reparto es anisotrópico, el reparto está relacionado con la clase de materia que produjo tal radiación, su densidad. ¡Ya veremos!
De todas las maneras, ¿No es una maravilla todo el Universo? El que nosotros, estemos aquí para contarlo así lo testifica.
Emilio Silvera V.
Nov
21
A veces nos podría dar la impresión de que, el Universo, nos esperaba
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)


Surgidos de la materia creada por el Universo pudimos alcanzar la inteligencia necesaria para hacer preguntas. Siempre digo que la materia “inerte” evolucionó hasta los pensamientos
En este lugar venimos hablando de cuestiones de Física, del Universo, de vez en cuando tocamos la I.A. y osamos comentar sobre la Conciencia y la Mente. Ante estas complejas cuestiones, el hecho mismo de que estemos aquí para plantearlas, como seres racionales y pensantes, es un auténtico milagro, ya que significa que deben haber ocurrido, necesariamente, complejas secuencias de sucesos para que a partir de la materia “inerte”, la mezcla de materiales complejos en condiciones excepcionales, hiciera surgir la vida.
Reparando en estas coincidencias cósmicas, el físico Freeman Dyson escribió en cierta ocasión:
“Cuando miramos en el universo e identificamos los muchos accidentes de la física y la astronomía que han colaborado en nuestro beneficio, casi parece que el universo debe haber sabido, en cierto sentido, que nosotros íbamos a venir“.
Particularmente, creo que la vida llegó a este planeta por una serie de circunstancias muy especiales: tamaño, temperatura y distancia al Sol (idónea para no morir congelados o asados por una temperatura extrema), su atmósfera primitiva, las chimeneas marinas, la mezcla de elementos, y su transformación evolutiva, el oxígeno, la capa de ozono, los mares y océanos ¡el agua!, etc, etc.

Este podría ser aquel protoplasma vivo del que surgió aquella primera célula replicante que comenzó, la aventura de la vida. En millones de años llegó hasta la conciencia.
Dada la inmensidad de nuestro universo, nuestro mismo caso (un sistema solar con planetas entre los que destaca uno que contiene vida inteligente), se habrá dado en otros muchos mundos similares o parecidos al nuestro, tanto en nuestra misma galaxia, la Vía Láctea, como en otras más lejanas. Me parece una estupidez que se pueda pensar que estamos solos en el universo; la lógica nos dice todo lo contrario.
Nuestro Sol, gracias al cual podemos existir, es una de las cien mil millones de estrellas que contiene nuestra Galaxia. Existen miles de millones de sistemas solares compuestos por estrellas y planetas como los nuestros. ¿En verdad se puede pensar que somos los únicos seres vivos inteligentes de la galaxia?

Me parece que no. Creo que estamos bien acompañados. Morfológicamente podrán ser distintos a nosotros pero, eso dependerá de la fuerza de Gravedad que emita el planeta que les acoja. Sin embargo, también, como nosotros, esas vidas estarán basadas en el Carbono. Digo esto porque, el Universo es igual en todas partes, no importa lo alejadas que estén sus regiones. Está regido por las mismas leyes y constantes y, precisamente por eso, lo que pasa “aquí” también pasará “!allí”.
La luz viaja por el vacío a 299.792,458 metros por segundo (300.000 Km/s). La estrella más cercana está a 4,2 años luz de nosotros. Con los ingenios actuales que corren a 60.000 KM/h. tardaríamos 30.000 años en llegar. ¿Cómo vamos a poder haber hecho ese contacto del que tanto hablamos?
El problema radica en que es difícil coincidir en el tiempo y en las enormes distancias que nos pueden separar. Cuántas Civilizaciones se habrán extinguidos y cuántas habrán surgido. Con las que se fueron se borraron todos sus logros y saberes y, las nuevas, estarán comenzando de nuevo ese difícil camino del saber. ¿El encuentro? ¡No será nada fácil que se produzca!
El tiempo y el espacio nacieron juntos cuando nació el universo en el Big Bang, llevan creciendo unos 13.500-18.000 millones de años y, tanto el uno como el otro, son enormes, descomunalmente grandes para que nuestras mentes lo asimilen de forma real.
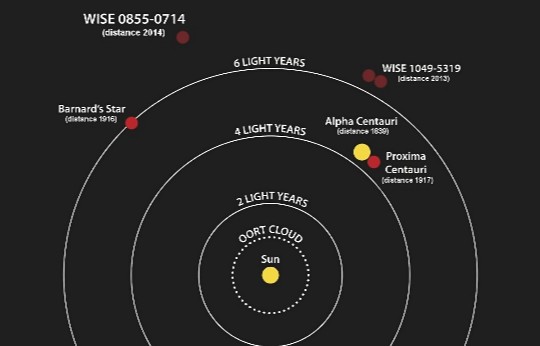
La estrella más cercana a nosotros, Alfa Centauri, está situada a una distancia de 4’3 años luz. El año luz es la distancia que recorre la luz, o cualquier otra radiación electromagnética, en un año trópico a través del espacio. Un año luz es igual a 9’4607×1012 Km, ó 63.240 unidades astronómicas, ó 0’3066 parsecs.
La luz viaja por el espacio a razón de 299.792.458 m/s, una Unidad Astronómica es igual a 150 millones de Km (la distancia que nos separa del Sol). El pársec es una unidad galáctica de distancias estelares, y es igual a 3’2616 años luz o 206.265 unidades astronómicas. Existen para las escalas galácticas o intergalácticas, otras medidas como el kilo-parsec (Kpc) y el mega-parsec (Mpc).
Nos podríamos entretener para hallar la distancia que nos separa de un sistema solar con posibilidad de albergar vida y situado a 118 años luz de nosotros. ¿Cuándo llegaríamos allí?

Nuestra nave llegará unas decenas de años
Es, claramente, la estrella más cercana al Sol, aunque su distancia esté en torno a los 40 billones (un 4 seguido por 13 ceros) de kilómetros, unos 4.35 años-luz. La tercera componente, no obstante, se encuentra algo más cercana, pues orbita a las otras dos y ahora se sitúa a unos 4.22 años-luz. Es llamada por eso Próxima Centauri. Ésta sí es, sin excepciones ni matices, la estrella que está más cerca de nuestro Sol.
Nuestros ingenios espaciales que enviamos a las lunas y planetas vecinos, viajan por el espacio exterior a 50.000/60.000 Km/h. Es una auténtica frustración el pensar lo que tardarían en llegar a la estrella cercana Alfa Centauri a más de 4 años luz.
Así que la distancia es la primera barrera infranqueable (al menos de momento). La segunda, no de menor envergadura, es la coincidencia en el tiempo. Se piensa que una especie tiene un tiempo limitado de existencia antes de que, por una u otra razón, desaparezca.

Nosotros mismos, si pensamos en el tiempo estelar o cósmico, llevamos aquí una mínima fracción de tiempo. Dadas las enormes escalas de tiempo y de espacio, es verdaderamente difícil coincidir con otras civilizaciones que, probablemente, existieron antes de aparecer nosotros o vendrán después de que estemos extinguidos. Por otra parte, el desplazarse por esas distancias galácticas de cientos de miles de millones de kilómetros, no parece nada fácil, si tenemos en cuenta la enorme barrera que nos pone la velocidad de la luz. Esta velocidad, según demuestra la relatividad especial de Albert Einstein, no se puede superar en nuestro universo.
Con este negro panorama por delante habrá que esperar a que un día en el futuro, venga algún genio matemático y nos de la fórmula para burlar esta barrera de la velocidad de la luz, para hacer posible visitar otros mundos poblados por otros seres. Por ahora, el único panorama creíble (dadas nuestras limitaciones físicas), está en los robots que, sin lugar a ninguna duda, serán la avanzadilla de la Humanidad en los viajes espaciales y, ellos serán los primeros en pisar otros mundos. De hecho, ahora mismo tenemos a Mars Phoenix investigando el suelo y la atmósfera de Marte y buscando vestigios de vida pasada o presente.


También cabe esperar que sean ellos (otros seres extraterrestres) los más adelantados y nos visiten a nosotros. Aunque, si tengo que ser sincero, preferiría no ser testigo nunca de una escena como la de arriba, en la que una nave alirnígena se acerca a la Tierra. Bastantes problemas nos creamos ya nosotros mismos para tener encima que bregar con otros venidos de fuera.
Si se tiene que producir ese encuentro, por mi parte, preferiría que seamos nosotros los visitantes. Me acuerdo de Colón, de Pizarro o Hernán Cortes e incluso de los ingleses en sus viajes de colonización, y la verdad, lo traslado a seres extraños con altas tecnologías a su alcance y con el dominio de enormes energías visitando un planeta como el nuestro, y dicho pensamiento no me produce la más mínima gracia. Más bien es gélido escalofrío.
Podrían responder a cualquier anatomía y… ¡sentimientos! Cualquier forma que nos podamos imaginar podría ser cierta. No sabemos lo que hí fuera nos podremos encontrar.
Según todos los indicios que la ciencia tiene en su poder, no parece que por ahora y durante algún tiempo, tengamos la posibilidad de contactar con nadie de más allá de nuestro sistema solar. Por nuestra parte existe una imposibilidad de medios. No tenemos aún los conocimientos necesarios para fabricar la tecnología precisa que nos lleve a las estrellas lejanas a la búsqueda de otros mundos. En lo que se refiere a civilizaciones extraterrestres, si las hay actualmente, no deben estar muy cerca; nuestros aparatos no han detectado señales que dejarían las sociedades avanzadas mediante la emisión de ondas de radio y televisión y otras similares. También pudiera ser, no hay que descartar nada, que estén demasiado adelantados para nosotros y oculten su presencia mientras nos observan, o atrasados hasta el punto de no emitir señales.


Nebulosa de la que un día hace 4.600 millones de años se formó la proto-estrella que sería el Sol


El Sol lleva 4.600 M de años enviando a la Tierra su luz y su calor. Cuando agote su combustible nuclear de fusión, se convertirá en una Gigante Roja que engullirá al planeta Mercurio y también a Venus. La Tierra se quedará muy cerca y completamente calcinada, la vida, tal como la conocemos desaparecerá
La gigante roja eyectará sus capas exteriores al Espacio Interestelar y formará una Nebulosa Planetaria. El resto de la masa de la estrella se comprimirá obligada por la fuerza de Gravedad y se convertirá en una estrella enana blanca que radiará furiosamente en el ultravioleta ionizando a la nebulosa.

Para cuando eso tenga que suceder, si queremos salvar a nuestra especie, ya habremos colonizadfos otros planetas.
De cualquier manera, por nuestra parte, sólo podemos hacer una cosa: seguir investigando y profundizando en el conocimiento del universo para desvelar sus misterios y conseguir algún día (aún muy lejano), viajar a las estrellas, única manera de escapar del trágico e inevitable final de nuestra fuente de vida, el Sol. Dentro de unos 4.000 millones de años, como ya he dicho antes (páginas anteriores), el Sol se transformará en una estrella gigante roja cuya órbita irá más allá de Mercurio, Venus y seguramente la Tierra. Antes, la temperatura evaporará toda el agua del planeta Tierra, la vida no será posible. El Sol explotará como estrella nova y lanzará sus capas exteriores al espacio exterior para que su viejo material forme nuevas estrellas. Después, desaparecida la fuerza de fusión nuclear, la enorme masa del Sol, quedara a merced de su propio peso y la gravedad que generará estrujará, literalmente, al Sol sobre su núcleo hasta convertirla en una estrella enana blanca de enorme densidad y minúsculo diámetro (en comparación con el original). Más tarde, la estrella se enfriará y pasará a engrosar la lista de cadáveres estelares.

Ciudades futuras en otros mundos
Para cuando ese momento este cercano, la humanidad, muy evolucionada y avanzada, estará colonizando otros mundos, tendrá complejos espaciales y ciudades flotando en el espacio exterior, como enormes naves-estaciones espaciales de considerables dimensiones que dará cobijo a millones de seres, con instalaciones de todo tipo que hará agradable y fácil la convivencia.
Modernas naves espaciales surcarán los espacios entre distintos sistemas solares y, como se ha escrito tantas veces, todo estará regido por una confederación de planetas en los que tomarán parte individuos de todas las civilizaciones que, para entonces, habrán contactado.
El avance en el conocimiento de las cosas está regida por la curiosidad y la necesidad. Debemos tener la confianza y la tolerancia, desechar los temores que traen la ignorancia, y, en definitiva, otorga una perspectiva muy distinta de ver las cosas y resolver los problemas. En tal situación, para entonces, la humanidad y las otras especie inteligentes tendrán instalado un sistema social estable, una manera de gobierno conjunto que tomará decisiones de forma colegiada por mayoría de sus miembros, y se vigilará aquellos mundos en desarrollo que, sin haber alcanzado el nivel necesario para engrosar en la Federación Interplanetaria de Mundos, serán candidatos futuros para ello, y la Federación vigilará por su seguridad y desarrollo en paz hasta que estén preparados.
En nuestro planeta pasan cosas que nos deben avergonzar. Pasamos junto a ellos como si fueran invisibles ¿Qué nos pasa?
También sabemos que el desconocimiento, el torpe egoísmo de unos pocos y sobre todo la ignorancia, es la madre de la desconfianza y, como ocurre hoy en pleno siglo XXI, los pueblos se miran unos a otros con temor; nadie confía a en nadie y en ese estado de tensión (que es el caso que se produce hoy día), a la más mínima salta una guerra que, por razones de religión mal entendida o por intereses, siempre dará el mismo resultado: la muerte de muchos inocentes que, en definitiva, nada tuvieron que ver en el conflicto. Los culpables e inductores, todos estarán seguros en sus refugios mientras mueren sus hermanos.
Es irrefutable esta desgraciada realidad que, sin que lo podamos negar, nos convierte en bárbaros mucho más culpables que aquellos de Atila, que al menos tenían la excusa de su condición primitiva y salvaje guiada por el instituto de la conquista y defensa de sus propias vidas.
¿Pero que excusa tenemos hoy?

El cometa se encontraba viajando entre las órbitas de Júpiter y de Marte. Mide unos cuatro kilómetros de diámetro, con una forma irregular.
Enviamos sondas espaciales a las lunas de Júpiter y al planeta Marte para que investiguen sus atmósferas, busquen agua y nos envíen nítidas fotografías de cuerpos celestes situados a cientos de millones de kilómetros de la Tierra.
Se construyen sofisticadas naves que surcan los cielos y los océanos llevando a cientos de pasajeros confortablemente instalados que son transportados de una a la otra parte del mundo.
Podemos transmitir imágenes desde Australia que en segundos pueden ser vistas en directo por el resto del mundo.
Tenemos en el espacio exterior telescopios como el Hubble y el James Webb, que nos envían constantemente al planeta Tierra imágenes de galaxias y sistemas solares situados a miles de millones de años luz de nosotros, y sin embargo, ¡¡medio mundo muere por el hambre, la miseria, la falta de agua y la enfermedad!!

¿Qué nos está pasando?
Aunque parezca que no tiene conexión alguna, la tiene y mucha, el conocimiento del Universo a través de la Astrofísica y la Astronomía, sin lugar a ninguna duda nos hará mejores, ya que, de ese conocimiento profundo nos vendrán otros relacionados que nos harán comprender también que, lo efímero de nuestras vidas, nos obliga, de alguna manera a ser mejores y que los errores cometidos son irreversibles y tal como marcha el tiempo (siempre adelante) no tenemos la oportunidad de reparar los daños.

Existe un principio de la física denominado Navaja de Ockham que afirma que siempre deberíamos tomar el camino más sencillo posible e ignorar las alternativas más complicadas, especialmente si las alternativas no pueden medirse nunca.
Para seguir fielmente el consejo contenido en la navaja de Ockham, primero hay que tener el conocimiento necesario para poder saber elegir el camino más sencillo, lo que en la realidad, no ocurre. Nos faltan los conocimientos necesarios para hacer las preguntas adecuadas.
Así que, siendo así las cosas el camino más aconsejable es el del conocimiento del mundo que nos rodea y del Universo que nos acoge, lo que nos lleva a tener la obligación de aprovechar el Año 2009 que ha sido nombrado como Internacional de la Astronomía, y, aprendamos del Universo, la Naturaleza es siempre la que nos trae las nuevas ideas, lo que, desde luego, no ocurre sin que la observemos.
Sobre el tema de los extraterrestres tengo serias dudas en lo que se refiere a que lleguemos nosotros a otro mundo habitado o que sean ellos los que lleguen al nuestro. Pienso que, si la Naturaleza ha querido que estemos tan separados… ¡Por algo será!
Emilio Silvera V.
Nov
21
¿La Curiosidad? ¡La madre del saber!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber del mundo ~
Clasificado en El saber del mundo ~
 Comments (0)
Comments (0)







Buscando Historias del Pasado

¡Qué bonito sería si las piedras pudieran hablar! ¿Qué nos contarían éstas?
Bueno, nos contarían como se paseaba Cristóbal Colón por el Monasterio de La Rábida en Palos de la Frontera, un pueblo de Huelva, de cuyo puerto se produjo la partida de Colón con los hermanos Pinzones en las tres Carabelas, Pinta, Niña y Santa María, hacia el Nuevo Mundo.

Grabado del inmueble publicado en el Semanario Pintoresco Español en 1849.




Los efectos del terremoto de Lisboa del año 1755 llegaron hasta este monasterio y obligó a reconstruir algunas de sus partes. Las paredes pintadas recordando el Descubrimiento.
Por unas módicas monedas, los Franciscanos que rigen el lugar y viven en el, regulan visitas al público y les guía explicando cada rincón del Monasterio y hablándole o contándoles episodios del pasado con Colón de personaje principal.

Los libros siempre fueron mis mejores amigos. No te comprometen a nada, te distraen y te enseñan, te hacen pasar maravillosas veladas, y, si eres listo (amigo), no olvides esta reseña.
Todos los asiduos a este lugar, sabéis de mi curiosidad insaciable por las cosas, por lo que pasó, por las Civilizaciones antiguas, por los misterios que la materia encierra, y, en fin, por el Universo y las historias de las criaturas que lo pueblan y que, en la antigüedad, estuvieron aquí. Cuando se tiene ante los ojos lugares que, como el que arriba podemos contemplar, nos transportan al pasado, primero lo miramos muy atentamente fijándonos en los detalles y, cerrando los ojos, podemos imaginar cómo las personas que hace muchos años estuvieron ahí, deambulaban y hacían su vida cotidiana dentro del entorno que les tocó vivir.
Templo Virupaksha (Hampi, India)
Baños árabes de Ronda Provincia de Málaga (España)
Biblioteca de Celso (Turquía
Coliseo de Roma (Italia)
Convento do Carmo (Lisboa, Portugal)
Machu Picchu (Perú)
Stonehenge (Amesbury, Reino Unido)
Anfiteatro romano de Cartagena (Murcia-España)
La Alcazaba de Almería (Andalucía-España)
Existen lugares en los que, se han conservado más vivos y realistas los recuerdos del pasado y, en la India, donde al contrario que en China, no cruzan el cielo los Dragones, serpientes o Aves monstruosas, nos dicen que fueron máquinas, las que, para el asombro de todos, cruzaban el cielo. ¿Cuántas leyendas, o, ¿historias? nos llegan del pasado… Será difícil discernir dónde está la realidad y comienza la imaginación.
el asombro de todos, cruzaban el cielo. ¿Cuántas leyendas, o, ¿historias? nos llegan del pasado… Será difícil discernir dónde está la realidad y comienza la imaginación.

James Churchward, el desconcertante estudioso inglés cuyas investigaciones no son nada desdeñables, siempre y cuando no se aproximan a las especulaciones teo-sofistas, nos habla de un manuscrito que contiene la descripción de una nave aérea de hace 20.000 años.
“La energía” –detalla en una obra redactada varios lustros antes de que se hablara de astronaves y satélites artificiales- se obtiene de la atmósfera de manera simple y poco costosa. En la obra daba una amplia explicación del motor y sus compartimentos y cámaras y de las increíbles propiedades que la nave tenía que, incluso, podía quedar estática en el aire, o, salir disparada como un rayo hacia lo más alto del cielo hasta desaparecer de la vista.
desaparecer de la vista.



Las Naves voladoras de los dioses, descritas en escritos Sanscritos
¿Fantasías? Escuchemos un relato de la Academia Internacional de Investigaciones sánscritas de Mysore: “Los manuscritos cuya traducción del sánscrito presentamos, describen varios tipos de “vimana” (naves que se mueven por sí mismas), capaces de viajar por su propio impulso por tierra, agua y aire, y, asimismo, de planeta a planeta. Parece que los vehículos aéreos podían detenerse en el cielo hasta quedar inmóviles, y que estaban dotados de instrumentos capaces de señalar, incluso a distancia, la presencia de aparatos enemigos.
quedar inmóviles, y que estaban dotados de instrumentos capaces de señalar, incluso a distancia, la presencia de aparatos enemigos.
(El relato fue publicado en la India por el especialista Maharshi Bharadaja con el título Aeronáutica del pasado prehistórico.)
Numerosísimos testimonios nos vienen a confirman ampliamente lo anterior. Por ejemplo tenemos una amplia muestra en el Samaranganasutradhara que narra la historia de vuelos fantásticos realizados por el mundo, y hacia el Sol y las estrellas. Un documento de época precristiana nos suministra una detallada descripción del carro celeste de Rama. La narración nos dice: “…el carro se movía por sí solo y era grande y estaba bien pintado; tenía dos pisos, muchas habitaciones y ventanas…”, cuyas hazañas, canta Valmiki el Heródoto indio: “El carro celeste, que posee una fuerza admirable, alada de velocidad, dorado en su forma y en su esplendor… El carro celeste ascendió por encima de la colina y del valle boscoso…alado como el rayo, dardo de Indra, fatal como el relámpago del cielo, envuelto en humo y destellos flameantes, rápida proa circular” (del Ramayana, que narra la epopeya de Rama).
y en su esplendor… El carro celeste ascendió por encima de la colina y del valle boscoso…alado como el rayo, dardo de Indra, fatal como el relámpago del cielo, envuelto en humo y destellos flameantes, rápida proa circular” (del Ramayana, que narra la epopeya de Rama).
Centenares y centenares de historias semejantes nos podemos encontrar a lo largo de las tradiciones hundúes: “ahí va la divina Maya volando en un carro de oro circular, que mide 12.000 codos de circunferencia, capaz de alcanzar las estrellas”, y, hete aquí el “caballo metálico del cielo” del rey Satrugit y el “carruaje del aire” del rey Pururavas. También el siglo IV de nuestra era encontramos a un héroe aeronauta, el monje budista Gunarvarman, quien se va desde Ceylán a Java en un aparato similar a los antiguos, sacado quién sabe de dónde.
en un aparato similar a los antiguos, sacado quién sabe de dónde.
Según se deduce de estos antiquísimos manuscritos en sánscrito, aquellos hindúes prehistóricos (o lo que realmente pudieran ser), no utilizaban aquellos ingenios voladores para excursiones de placer, sino que, según nos cuentan los relatos, las acciones bélicas eran también cotidianas que describen terribles batallas.
excursiones de placer, sino que, según nos cuentan los relatos, las acciones bélicas eran también cotidianas que describen terribles batallas.
Un bajorrelieve en Angkor Wat (Camboya) representa a Rávana Rávana peleando en la batalla de Lanka, el clímax del Ramaiana.
Rávana, el rey de los demonios de Ceylán, enemigo mortal de Rama, “voló sobre los adversarios (según nos narra un manuscrito del año 500 a, de C.) haciendo caer ingenios que causaron grandes destrucciones. Finalmente, fue capturado y muerto, y su máquina celeste cayó en manos del capitán hindú Ram Chandra, quién, sirviéndose de ella, voló a la capital, Adjhudia…”
Agni (Sanscrito: significa fuego y señala al dios védico del fuego en el hinduísmo
Y esto no son más que bagatelas. “El Bhisma Parva –recuerda Drake- menciona armas como la “verga de Brahma” y el “Rayo de Indra”, cuyos efectos se parecen a los producidos por la energía nuclear. El Drona Parva nos habla del “señor Mahadeva” y de sus terribles lanzas volantes (¿misiles?) capaces de destruir ciudades enteras fortificadas…, y describe las fantásticas armas de Agni, que aniquilaron ejércitos completos y devastaron la Tierra como
la “verga de Brahma” y el “Rayo de Indra”, cuyos efectos se parecen a los producidos por la energía nuclear. El Drona Parva nos habla del “señor Mahadeva” y de sus terribles lanzas volantes (¿misiles?) capaces de destruir ciudades enteras fortificadas…, y describe las fantásticas armas de Agni, que aniquilaron ejércitos completos y devastaron la Tierra como bombas de Hidrógeno.”
bombas de Hidrógeno.”
¿Es posible que no se hayan conservado trazas de estos alucinantes conflictos? Los restos existen, y numerosísimos –responden los investigadores-. Basta que nos tomemos la molestia de ir en su busca. No es una empresa fácil, desde luego, puesto que, desde hace milenios la jungla se ha espesado sobre las ruinas, pero si consiguiéramos localizar todas las “ciudades muertas” de la gran península, constelaríamos el mapa de la India de tantos puntos como los que, en un Atlas, nos indican los centros de población actuales.
luego, puesto que, desde hace milenios la jungla se ha espesado sobre las ruinas, pero si consiguiéramos localizar todas las “ciudades muertas” de la gran península, constelaríamos el mapa de la India de tantos puntos como los que, en un Atlas, nos indican los centros de población actuales.

De vez en cuando aparecen descripciones a este respecto que nos dejan perplejos. El explorador De Camp, por ejemplo, refirió haber visto, en la zona que se extiende entre el Ganges y los montes Rajmahal, ruinas carbonizadas por algo que no podía ser un simple incendio, por violento que éste fuera. Algunas piedras gigantescas aparecían fundidas y desenterradas en varios puntos, “como bloques de estaño afectados por la salpicadura de una colada de acero”.
el Ganges y los montes Rajmahal, ruinas carbonizadas por algo que no podía ser un simple incendio, por violento que éste fuera. Algunas piedras gigantescas aparecían fundidas y desenterradas en varios puntos, “como bloques de estaño afectados por la salpicadura de una colada de acero”.
Más al Sur, el oficial británico J. Campbell se topó, en los años veinte, con ruinas similares, y quedó sorprendido por un extrañísimo detalle: en el pavimento semivitrificado de lo que debió de ser un patio interior, parecían haber sido impresas, por una fuerza desconocida, formas de cuerpos humanos.
veinte, con ruinas similares, y quedó sorprendido por un extrañísimo detalle: en el pavimento semivitrificado de lo que debió de ser un patio interior, parecían haber sido impresas, por una fuerza desconocida, formas de cuerpos humanos.

Inmensos edificios de piedra comidos por la vegetación y el paso del tiempo
Otros viajeros refieren haber descubierto en el corazón de los bosques indios ruinas de edificios nunca vistos, con paredes “semejantes a gruesas losas de cristal” asimismo perforadas, resquebrajadas y corroídas por agentes desconocidos. Y habiendo penetrado en una de estas construcciones, parecida a una cúpula baja, el explorador y cazador H. J. Hamilton se encontró con la mayor sorpresa de su vida.
“En una parte –recuerda-, el suelo cedió bajo mis pies con un extraño crujido. Me puse a seguro y, luego, ensanché con la culata del fusil el boquete que se había abierto, y me introduje en él. Me encontré en una estancia larga y estrecha que recibía luz por una grieta de la bóveda. Al fondo, vi una especie de mesa y un asiento del mismo “cristal” de que estaban hechas las paredes.
En el asiento, se enroscaba una forma extraña, de contornos vagamente humanos. Observándola de cerca, me pareció, al principio, que se trataba de una estatua deteriorada por la acción del tiempo, pero, luego, descubrí algo que me llenó de horror: bajo el “vidrio” que revestía aquella estatua, ¡se podían distinguir claramente los detalles del esqueleto!”.
Muros, muebles y seres humanos vitrificados… ¿Qué tremendos secretos se esconden entre las líneas del Mahabrata y del Drona Parva?
“En los textos religiosos hindúes se describen con gran detalle aparatos voladores con terribles armas. Sobre todo en los Vedas, que se tienen por las fuentes más antiguas. La palabra veda significa «conocimiento sagrado». Uno de estos textos, el Rigveda, es una colección de 1.028 himnos a los dioses. Afirma sin ambigüedades que estas máquinas voladoras venían del cosmos a la Tierra y que los dioses descendieron personalmente a impartir conocimientos a los seres humanos. Del mismo modo que en las leyendas judías, en los textos hindúes se describen batallas entre los dioses; pero no en un cielo indefinido de gloria espiritual, sino «en el firmamento sobre la Tierra». En el «Vanaparvan», que pertenece al Mahabharata hindú, se describen las residencias de los dioses como lugares situados en el espacio, que giraban en órbita muy por encima de la Tierra. Lo mismo puede
los dioses; pero no en un cielo indefinido de gloria espiritual, sino «en el firmamento sobre la Tierra». En el «Vanaparvan», que pertenece al Mahabharata hindú, se describen las residencias de los dioses como lugares situados en el espacio, que giraban en órbita muy por encima de la Tierra. Lo mismo puede encontrarse en el Sabhaparva. Estas enormes estaciones espaciales tenían nombres tales como Vaihayasu, Gaganacara y Khecara. Eran tan grandes que las naves-lanzadera, llamadas vimanas, podían entrar en su interior por enormes puertas.”
encontrarse en el Sabhaparva. Estas enormes estaciones espaciales tenían nombres tales como Vaihayasu, Gaganacara y Khecara. Eran tan grandes que las naves-lanzadera, llamadas vimanas, podían entrar en su interior por enormes puertas.”

Cuando uno lee todas estas “historias”, no sería nada extraño que al quedar profundamente dormidos, nuestra mente regrese a los recuerdos de lo que allí le contaron y pueda imaginarse que vienen visitantes no invitados. Nunca podremos poner freno a nuestros pensamientos, es la única libertad real de la que podemos disponer, se generan sin que podamos remediarlo y, para nosotros, en exclusiva, escenifican los más variados, extraños, o, cotidianos escenarios. Esos pensamientos imaginativos reflejan nuestras inquietudes pero, también, no pocas veces, nos hablan de cosas que no podemos explicar.
Historias y leyendas extrañas para nosotros los occidentales, culturas distintas a la nuestra que, sin embargo, buscan las mismas cosas, sienten la misma curiosidad, y, sus pensadores nos hablan de cosas profundas. No olvidemos que en la India se habló por vez primera del átomo, del vacío, y, también allí se utilizó por vez primera el número Cero.
Emilio Silvera Vázquez
Nov
21
¡El Universo y la Mente! Una prueba de la evolución de la materia hasta...
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo y la Mente ~
Clasificado en El Universo y la Mente ~
 Comments (1)
Comments (1)
Nos dicen que todo surgió a partir de una singularidad, un punto de una densidad y energía infinita. Algo parecido a una enorme fluctuación del Vacío que creó el Espacio y el Tiempo, surgieron las partículas y la materia acompañada de grandes energías… ¡después, el Tiempo trajo todo lo demás!



¡El Universo y la Mente! Una prueba de la evolución de la materia hasta la consciencia
Es verdaderamente admirable constatar cómo ha ido evolucionando nuestro entendimiento del mundo que nos rodea, de la Naturaleza, del Universo. Hubo un tiempo en el que, los individuos de nuestra especie deambulaban por el planeta pero no sabían comprender el “mundo”, ni podían pensar siquiera en el misterio que representaban los fenómenos naturales que a su alrededor se sucedían.
Pasado el tiempo, pudieron mirar hacia arriba y, la presencia de aquellos puntitos brillantes en la oscura y misteriosa oscuridad de la noche, el paso de los cometas, y otras maravillas que no podían explicar, despertó su curiosidad consciente y comenzaron a plantearse algunas preguntas. Muchas decenas de miles de más tarde, nuestro deambular por el planeta, las experiencias y la observación de la Naturaleza, nos llevó a comprender, algunas de las cosas que antes no tenían explicación.
Fueron dejando huellas de lo que en el cielo veían
Pensadores del pasado dejaron la huella de sus inquietudes y los llamados filósofos naturales, hicieron el ejercicio de dibujar el “mundo” según ellos lo veían. Nos hablaron de “elementos” de “átomos” y, aunque no era el concepto que ahora de esas palabras podamos tener, ya denotaba una gran intuición en el pensamiento humano que trataba de entender la Naturaleza y cómo estaban hechas las cosas que nos rodeaban. Ellos, a la materia primigenia la llamaron “Ylem” la sustancia cósmica.
Es cierto que siempre hemos quertido abarcar más de lo que nuestra “sabiduría” nos podía permitir. Ahora, en el presente, las cosas no han cambiado y tratamos de explicar lo que no sabemos, y, para ello, si hay que inventarse la “materia oscura”, las “fluctuaciones de vacío”, los “universos paralelos”, los “agujeros de gusano”, o, cualesquiera otros conceptos o fenómenos inexistentes en el mundo material o experimental… ¡qué más da! Lo importante es exponer las ideas que nos pasen por la cabeza que, de alguna manera, pasando el tiempo, se harán realidad. Nuestras mentes, como digo, siempre fueron por delante de nosotros mismos y ha dejado al descubierto esa intuición que nos caracteriza y que, de alguna manera, nos habla de esos hilos invisbles que, no sabemos explicar como pero, nos conectan con el resto del Universo del que, al fin y al cabo, formamos parte, ¡la que piensa!

Tales de Mileto, uno de los siete sabios de Grecia, nos habló de la importancia del agua para la vida. Él intuyó que sin agua, la vida sería estéril en el planeta. Allí donde el agua corria y se mezclaba con las sustancias de la tierra, unido a los fenómenos naturales y ayudada por el tiempo, hacía posible el surgir de la vida.
Ahora, que hemos podido realizar un cierto avance en el “conocimiento del mundo que nos rodea”, no le damos la verdadera importancia que tienen algunos pensamientos del pasado que, en realidad, son los responsables de que ahora, nos encontremos en el nivel de conocimiento que hemos podido conquistar. Tales de Mileto, uno de los siete sabios de Grecia, fue el primero que dejó a un lado la mitología para utilizar la lógica y, entre otras muchas cosas, indicó la importancia que tenía el agua para la existencia de la vida. Empédocles nos habló de los elementos y Demócrito del a-tomo o átomo., Arquitas de Tarento (filósofo, soldado y músico), el amigo de Platón y seguidor de Pitágoras, ya se preguntaba: ¿Es el Universo infinito?

Él mismo se contestaba diciendo que todo tenía un límite y pensaba en el final que lindaba con el “vacío”, allí donde nada impedía que su espada, lanzada con fuerza en el borde del universo, siguiera su camino sin fin, ninguna fuerza podría pararla y con ninguna clase de materia podría chocar. Así, con esos pensamientos surgidos de la mente humana, podemos constatar que, desde siempre, hemos tratado de saber de qué están hechas las cosas, cómo funciona la Naturaleza y de qué manera funciona el universo que tratamos de comprender.
El Universo se expande y nuestras mentes también. Eso que llamamos Tiempo siguió su transcurrir inexorable, los pensamientos de los grandes pensadores se fueron acumulando en un sin fin de conjeturas y teorías que, poco a poco, pudimos ir comprobando mediante la observación, el estudio y la experimentación hasta que pudimos llegar a saber de qué estaban hechas las estrellas y cómo la materia se transmutaba en sus “hornos” nucleares para crear elementos que hicieran posible el surgir de la vida en los mundos (no creo que la vida esté supeditada a este mundo nuestro).
Puede estar representada de muchas maneras pero, materia es
“Materia es todo aquello que tiene localización espacial, posee una cierta cantidad de energía, y está sujeto a cambios en el tiempo y a interacciones con aparatos de medida. En física y filosofía, materia es el término para referirse a los constituyentes de la realidad material objetiva, entendiendo por objetiva que pueda ser percibida de la misma forma por diversos sujetos. Se considera que es lo que forma la parte sensible de los objetos perceptibles o detectables por medios físicos. Es decir es todo aquello que ocupa un sitio en el espacio, se puede tocar, se puede sentir, se puede medir, etc.”
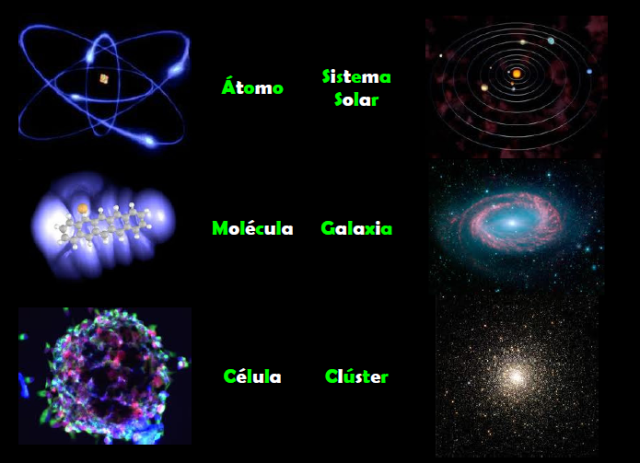
El conocimiento que creemos que tenemos sobre cómo está conformada la materia y las fuerzas fundamentales que con ella interaccionan, nos ha llevado a escenificar un Universo algo más comprensible que aquel, que nuestros ancestros imaginaron con la presencia de dioses y divinidades que eran los que, creaban los “mundos” o, el universo mismo, cada vez que soñaban. Es asombroso que hayamos podido llegar hasta la consciencia siendo la línea de salida la “materia inerte”. Sin embargo, el recorrido ha sido arduo y muy largo…, ¡diez mil millones de años han necesitado las estrellas para poder solidificar los elementos de la vida para crear, en algunos de los muchos mundos presentes en las galaxias, el protoplasma vivo que diera lugar a esa primera célula replicante que comenzara la fascinante aventura de la vida hasta llegar a los pensamientos.

Si pensamos en la presencia de la Vida, el camino tan complejo que ha tenido que seguir para poder llegar, la cantidad de parámetros que han tenido que ser ajustados para su presencia… ¡Uno está tentado a pensar que existe una Conciencia Cósmica!
Si nos preguntaran: ¿Es consciente el Universo? Tendríamos que contestar de manera afirmativa, toda vez que, al menos una parte, ¡la que piensa!, representada por seres vivos y que forman parte de ese inmenso universo, sí que lo es. La vida es la consecuencia de la materia evolucionada hasta su más alto nivel y, a partir de ella, ha podido surgir eso que llamamos cerebro del que surge el concepto de mente, ese ente inmaterial y superior que trasciende y va más allá, lo que los filósofos llamaron Ser y quisieron explicar mediante la metafísica. Todavía, no sabemos lo que la vida es y tampoco, podemos explicar, lo que es la energía, o, por exponer algún concepto de los muchos que denota nuestra ignorancia, tampoco podemos contestar a una simple pregunta: ¿Qué es el Tiempo? ¿Existe en realidad o simplemente es una abstracción de la mente?

Lo cierto es que nuestra especie ha dejado profundas huellas de su deambular por el mundo. Muchos de sus “tesoros y obras” quedaron enterrados en las profundidades del tiempo o inundados por los diluvios que las distintas civilizaciones que fueron nos contaron con sus maravillosas leyendas que, en realidad, trataban de explicar algo que sucedió y que no llegaban a comprender y, para ello, inventaban bonitas historias en las que, narraban hechos que quedaron difuminados por la fantasía hasta el punto de no saber, en el presente, donde termina la realidad y comienza la leyenda y si eran ciertas o no las bonitas “historias” que nos contaron.
Lo cierto es que con frecuencia sucede que al surgir ideas nuevas que tienden a querer explicar científicamente lo que es la Naturaleza, aparecen viejos datos que relacionan esas nuevas ideas con aquellos viejos problemas. Tenemos que admitir que todavía “no sabemos” cómo es la realidad del mundo y que, nuestra realidad, no tiene que coincidir con la verdadera realidad que incansables buscamos y que, no siempre podemos “ver” aunque la tengamos delante de nuestros propios ojos.
De hecho, no sabemos explicar ni cómo se pudieron formar las galaxias, y, a pesar de ello, no tenemos empacho de hablar de singularidades y agujeros de gusano o de universos paralelos. ¡La imaginación!, creo que sin ella, no habríamos podido llegar hasta aquí. La imaginación unida a la curiosidad ha sido desde siempre, el motor que nos llevó hacia el futuro.
Si en realidad existe “el infinito”, seguro que está en nuestras mentes, o, posiblemente en otras que, como las nuestras, han imaginado cómo ensanchar el mundo y universo de los pensamientos sin límite alguno, el único límite que existe, amigos míos, es el de nos impone nuestra ignorancia para llegar a comprender lo que la Naturaleza es. En la Naturaleza están todas las respuestas a las preguntas que planteamos y que nadie sabe contestar. En ella, en la Naturaleza, buscan nuestros sabios esas respuestas y, para poder encontrarlas hemos inventado los aceleradores de partículas, los microscopios y telescopios que nos llevan a ese “otro universo” que el ojo desnudo no puede ver pero que, no deja de ser nuestro propio mundo, y, al ser conscientes de ello, también lo somos de nuestras limitaciones. En realidad, la única manera de avanzar es ser consciente de que no sabemos, toda vez que, si creyéramos que ya lo sabiamos todo… ¿para qué seguir buscando?
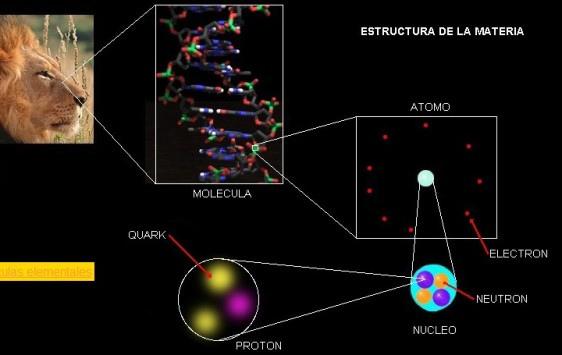
Todo está hecho de Quarks y Leptones, desde una galaxia hasta el fiero león que habita en la selva, también un vaso de leche, mi mesa escritorio, el suelo que pisamos que, por cierto, nos sostiene y nos da la sensación de firmeza debido a que, los átomos que lo conforman, por el bullir de los electrones, han creado un campo magnético que nos da esa sensación, cuando en realidad, casi todo son espacios vacíos.
¡Qué cosas!

El pensamiento filosófico es un “mundo” que ensanchó los límites de la mente humana, nos llevó hasta la Ciencia, en un mundo en el que, las semillas de Quarks y Leptones se constituían en un universo material en el que, unas fuerzas fundamentales interaccionaban para hacer posible el ritmo de todo lo que podemos observar, de todo lo que existe y que llegó, a crear el espacio-tiempo y dentro de toda esa inmensidad, ¡los pensamientos y la imaginación! de objetos complejos que llamamos cerebro y transportan mentes creadoras de ideas como la de universos en la sombra, cuerdas cósmicas y otros muchos fantásticos fenómenos que pueblan un paisaje inmenso de “cosas” en constante ebullición que se transforman para crear otras diferentes. Para que eso sea posible, a veces podemos contemplar lugares violentos donde impera un Caos aparente pero, necesario para la creación.
Estamos rodeados de cosas bellas presentes en cualquier lugar al que podamos mirar pero… ¿Prestamos atención?
“Todas las cosas son”
Con esas sencillas palabras, el sabio, elevó a todas las cosas a la categoría de SER. ¿Tendrá memoría la materia? ¿Será posible que eso que llamamos materia “inerte”, no sea en realidad tan inocua ni tan insensible como imaginamos? Es posible que cada de la materia sea un paso necesario para poder llegar hasta su estado de consciencia que, en este mundo, se ha revelado en nosotros.

Y, en todo ese aparente maremágnum, apareció la vida. “La Vida, una cúpula de vidrio multicolor, mancha el blanco resplandor de la eternidad.” De la misma manera que no llegamos a comprender el Universo, tampoco conocemos lo que la vida es, y, hasta las definiciones que hemos encontrado para explicarla, ni se acercan a la realidad, a la grandiosidad, a la maravillosa verdad que el universo nos muestra a través de la vida, en la que, a veces, subyacen los pensamientos y los mejores sentimientos.

Sí, amigos, son muchas las razones que tenemos para pensar. Sin embargo, la mayoría de las veces, no tenemos el tiempo necesario para ellos, nos falta tranquilidad, los problemas cotidianos nos absorben y preocupan (La hipoteca, me van a despedir, necesito una subida d sueldo, este niño no estudia, el novio de la niña no nos gusta….), muchos son los problemas que, por lo general, tenemos todos como para ponernos a pensar en todas estas cuestiones tan interesantes de la Naturaleza, del mundo en el que vivimos y del Universo que nos acoge, y, es una pena. Todos deberíamos tener un conocimiento básico del entorno natural en el que vivimos, y, del sistema solar al que pertenecemos, del Grupo Local de Galaxias en el que está la Vía Láctea, y, más allá, de todas las maravillas que están esperando que las descubramos.
Conocer el Universo es una obligación, al menos los detalles más básicos.
Emilio Silvera Vázquez
Nov
21
El fino equilibrio que permite la presencia de la Vida
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo dinámico ~
Clasificado en El Universo dinámico ~
 Comments (2)
Comments (2)
- La primera galaxia con tres agujeros negros en su centro
- Detectan una enorme explosión termonuclear en el espacio
- La Cosmología, en crisis: el Universo se expande más deprisa de lo que se creía



Hay que reseñar que, solo en la Vía Láctea, existen unos 30.000 millones de estrellas como el Sol
Las estrellas típicas como el Sol, emiten desde su superficie un viento de partículas cargadas eléctricamente que barre los atmósferas de los planetas en órbitas a su alrededor y a menos que el viento pueda ser desviado por un campo magnético, los posibles habitantes de ese planeta lo podrían tener complicado soportando tal lluvia de radiactividad. En nuestro sistema solar el campo magnético de la Tierra ha protegido su atmósfera del viento solar, pero Marte, que no está protegido por ningún campo magnético, perdió su atmósfera hace tiempo.
Hasta el momento sólo sabemos de la vida en la Tierra
Probablemente no es fácil mantener una larga vida en un planeta del Sistema solar. Poco a poco hemos llegado a apreciar cuán precaria es. Dejando a un lado los intentos que siguen realizando los seres vivos de extinguirse a sí mismos, agotar los recursos naturales, propagan infecciones letales y venenos mortales y emponzoñar la atmósfera, también existen serias amenazas exteriores.
Los movimientos de cometas y asteroides, a pesar de tener la defensa de Júpiter, son una seria y cierta amenaza para el desarrollo y persistencia de vida inteligente en las primeras etapas. Los impactos no han sido infrecuentes en el pasado lejano de la Tierra habiendo tenido efectos catastróficos. Somos afortunados al tener la protección de la luna y de la enorme masa de Júpiter que atrae hacia sí los cuerpos que llegan desde el exterior desviándolos de su probable trayectoria hacia nuestro planeta.
La caída en el Planeta de uno de estos enormes pedruscos podría producir extinciones globales y retrasar en millones de años la evolución.


:format(jpg)/f.elconfidencial.com%2Foriginal%2Fbaa%2Faf2%2F3d2%2Fbaaaf23d21f5d5fddf2c07cafe37bac3.jpg)
Cuando comento éste tema no puedo evitar el recuerdo del meteorito caído en la Tierra que impactó en la península de Yucatán hace 65 millones de años, al final de la Era Mesozoica, cuando según todos los indicios, los dinosaurios se extinguieron. Sin embargo, a aquel suceso catastrófico para los grandes lagartos, en realidad supuso que la Tierra fue rescatada de un callejón sin salida evolutivo. Parece que los dinosaurios evolucionaron por una vía que desarrollaba el tamaño físico antes que el tamaño cerebral.
La desaparición de los dinosaurios junto con otras formas de vida sobre la Tierra en aquella época, hizo un hueco para la aparición de los mamíferos. Se desarrollo la diversidad una vez desaparecidos los grandes depredadores. Así que, al menos en este caso concreto, el impacto nos hizo un gran favor, ya que, hizo posible que 65 millones de años más tarde pudiéramos llegar nosotros. Los dinosaurios dominaron el planeta durante 150 millones de años; nosotros, en comparación, llevamos tres días y, desde luego, ¡la que hemos formado!
La Tierra se fue enfriando, se formaron los océanos y la atmósfera, los elementos para la vida (la química de las estrellas), estaban en la Tierra joven que, situada en la zona habitable de la estrellas, pudo ofrecer las condiciones para el surgir de la vida que, a partir de la materia “inerte” evolucionada… ¡Fue imparable en todas sus formas y en todas sus especies!
Y… Aquí estamos.
En nuestro sistema solar la vida se desarrolló por primera vez sorprendentemente pronto tras la formación de un entorno terrestre hospitalario. Hay algo inusual en esto. El secreto reside en el tiempo biológico necesario para desarrollar la vida y el tiempo necesario para desarrollar estrellas de segunda generación y siguientes que en novas y supernovas cristalicen los materiales complejos necesarios para la vida, tales como el hidrógeno, nitrógeno, oxígeno, carbono, etc.
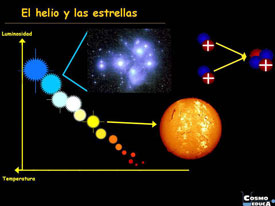


Parece que la similitud en los “tiempos” no es una simple coincidencia. El argumento, en su forma más simple, lo introdujo Brandon Carter y lo desarrolló John D. Barrow por un lado y por Frank Tipler por otro. Al menos, en el primer sistema Solar habitado observado ¡el nuestro!, parece que sí hay alguna relación entre t(bio) y t(estrella) que son aproximadamente iguales el t(bio) –tiempo biológico para la aparición de la vida- algo más extenso.

La evolución de una atmósfera planetaria que sustente la vida requiere una fase inicial durante la cual el oxígeno es liberado por la foto-disociación de vapor de agua. En la Tierra esto necesitó 2.400 millones de años y llevó el oxígeno atmosférico a aproximadamente una milésima de su valor actual. Cabría esperar que la longitud de esta fase fuera inversamente proporcional a la intensidad de la radiación en el intervalo de longitudes de onda del orden de 1000-2000 ángstroms, donde están los niveles moleculares clave para la absorción de agua.
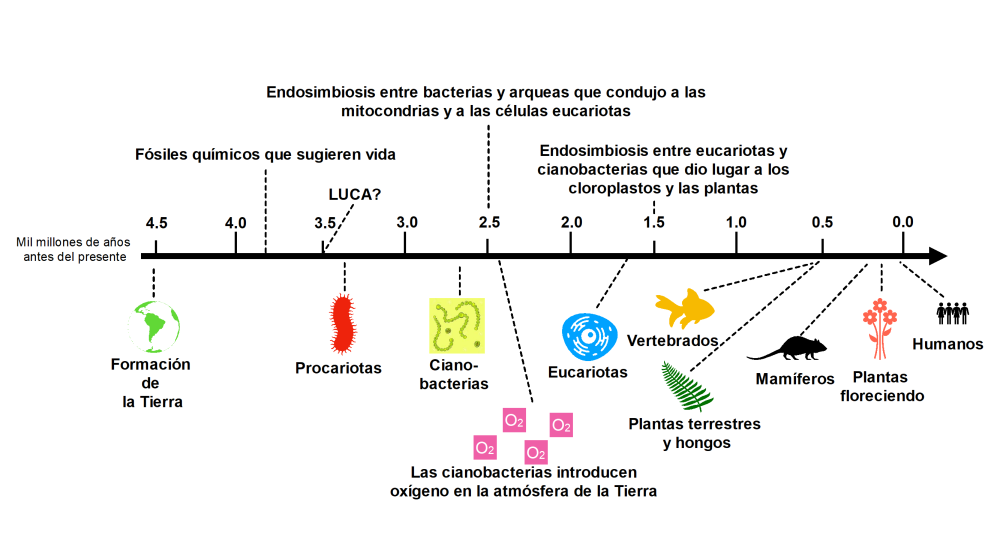
Este simple modelo indica la ruta que vincula las escalas del tiempo bioquímico de evolución de la vida y la del tiempo astrofísico que determina el tiempo requerido para crear un ambiente sustentado por una estrella estable que consume hidrógeno en la secuencia principal y envía luz y calor a los planetas del Sistema Solar que ella misma forma como objeto principal.
A muchos les cuesta trabajo admitir la presencia de vida en el Universo como algo natural y corriente, ellos abogan por la inevitabilidad de un Universo grande y frío en el que, es difícil la aparición de la vida, y, en el supuesto de que ésta aparezca, será muy parecida a la nuestra.

Creo que la clave está en los compuestos del carbono, toda la vida terrestre actualmente conocida exige también el Agua como disolvente. Y como para el carbono, se supone a veces que el agua es el único producto químico conveniente para cumplir este papel. El amoníaco (el nitruro de hidrógeno) es la alternativa ciertamente al agua, la más generalmente posible propuesta como disolvente bioquímico. Numerosas reacciones químicas son posibles en disolución en el amoníaco, y el amoníaco líquido tiene algunas semejanzas químicas con el agua. El amoníaco puede disolver la mayoría de las moléculas orgánicas al menos así como el agua, y por otro lado es capaz de disolver muchos metales elementales. A partir de este conjunto de propiedades químicas, se teorizó que las formas de vida basada en el amoníaco podrían ser posibles. También se dijo del Silicio. Sin embargo, ninguno de esos elementos son tan propicios para la vida como el Carbono y tienen, como ya sabemos, parámetros negativos que no permiten la vida tal como la conocemos.

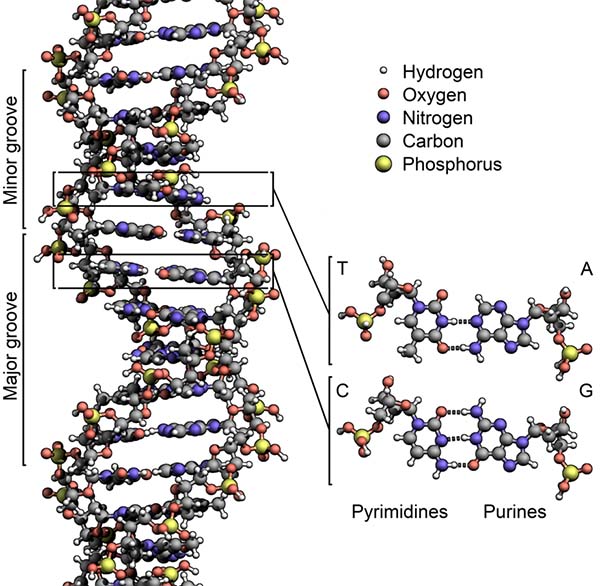
Hasta el momento, todas las formas de vida que surgieron en la Tierra, están basadas en el Carbono.
Los biólogos, sin embargo, parecen admitir sin problemas la posibilidad de otras formas de vida, pero no están tan seguros de que sea probable que se desarrollen espontáneamente, sin un empujón de formas de vida basadas en el carbono. La mayoría de los estimaciones de la probabilidad de que haya inteligencias extraterrestres en el Universo se centran en formas de vida similares a nosotras que habiten en planetas parecidos a la Tierra y necesiten agua y oxígeno o similar con una atmósfera gaseosa y las demás condiciones de la distancia entre el planeta y su estrella, la radiación recibida, etc. En este punto, parece lógico recordar que antes de 1957 se descubrió la coincidencia entre los valores de las constantes de la Naturaleza que tienen importantes consecuencias para la posible existencia de carbono y oxígeno, y con ello para la vida en el Universo.
Hay una coincidencia o curiosidad adicional que existe entre el tiempo de evolución biológico y la astronomía. Puesto que no es sorprendente que las edades de las estrellas típicas sean similares a la edad actual del Universo, hay también una aparente coincidencia entre la edad del Universo y el tiempo que ha necesitado para desarrollar formas de vida como nosotros.

Poco después, surgirían las primeras células replicantes que evolucionaron hacia nosotros

Homo sapiens
Si miramos retrospectivamente cuánto tiempo han estado en escena nuestros ancestros inteligentes (Homo sapiens) vemos que han sido sólo unos doscientos mil años, mucho menos que la edad del Universo, trece mil millones de años, o sea, menos de dos centésimos de la Historia del Universo. Pero si nuestros descendientes se prolongan en el futuro indefinidamente, la situación dará la vuelta y cuando se precise el tiempo que llevamos en el Universo, se hablará de miles de millones de años.


-
C: Carbono
-
H: Hidrógeno
-
O: Oxígeno
-
N: Nitrógeno
-
P: Fósforo
-
Fe: Hierro
-
S: Azufre
-
Ca: Calcio
-
I: Yodo
-
Na: Sodio
-
K: Potasio
-
Cl: Cloro
-
Mg: Magnesio
-
F: Flúor
-
Cu: Cobre
-
Zn: Zinc
-
Glúcidos o Hidratos de Carbono
-
Lípidos
-
Proteínas
-
Ácidos Nucleicos
A veces, nuestra imaginación dibuja mundos de ilusión y fantasía pero, en realidad… ¿serán sólo sueños?, o, por el contrario, pudieran estar en alguna parte del Universo todas esas cosas que imaginamos aquí y que pudieran estar presentes en otros mundos lejanos que, como el nuestro…posibilito la llegada de la vida.


Sí, imaginamos demasiado pero… ¿Qué hay más poderoso que la imaginación?
Brandon Carter y Richard Gott han argumentado que esto parece hacernos bastante especiales comparados con observadores en el futuro muy lejano.


Lo que no sabemos es si, los observadores del futuro serán hombres o máquinas, aunque sospecho que lo segundo, ya que, en el Presente, ya nos multan las máquinas situadas en las carreteras.
¿Cuántos secretos están en esos números escondidos? La mecánica cuántica (h), la relatividad (c), el electromagnetismo (e–). Todo eso está ahí escondido. El número 137 es un número puro y adimensional, nos habla de la constante de estructura fina alfa (α), y, el día que sepamos desentrañar todos sus mensajes… ¡Ese día sabremos!
Extraños mundos que pudieran ser
Podríamos imaginar fácilmente números diferentes para las constantes de la Naturaleza de forma tal que los mundos también serían distintos al planeta Tierra y, la vida no sería posible en ellos. Aumentemos la constante de estructura fina más grande y no podrá haber átomos, hagamos la intensidad de la gravedad mayor y las estrellas agotarán su combustible muy rápidamente, reduzcamos la intensidad de las fuerzas nucleares y no podrá haber bioquímica, y así sucesivamente.
Hay cambios infinitesimales que seguramente podrían ser soportados sin notar cambios perceptibles, como por ejemplo en la vigésima cifra decimal de la constante de estructura fina. Si el cambio se produjera en la segunda cifra decimal, los cambios serían muy importantes. Las propiedades de los átomos se alteran y procesos complicados como el plegamiento de las proteínas o la replicación del ADN pueden verse afectados de manera adversa. Sin embargo, para la complejidad química pueden abrirse nuevas posibilidades. Es difícil evaluar las consecuencias de estos cambios, pero está claro que, si los cambios consiguen cierta importancia, los núcleos dejarían de existir, n se formarían células y la vida se ausentaría del planeta, siendo imposible alguna forma de vida.
“Es difícil formular cualquier teoría firme sobre las etapas primitivas del universo porque no sabemos si hc/e2 es constante o varía proporcionalmente a log(t). Si hc/e2 fuera un entero tendría que ser una constante, pero los experimentadores dicen que no es un entero, de modo que bien podría estar variando. Si realmente varía, la química de las etapas primitivas sería completamente diferente, y la radiactividad también estaría afectada. Cuando empecé a trabajar sobre la gravedad esperaba encontrar alguna conexión ella y los neutrinos, pero esto ha fracasado.”
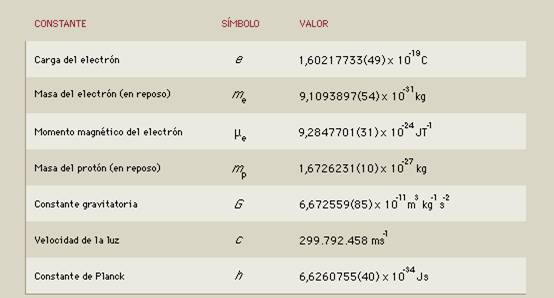
Las constantes de la naturaleza ¡son intocables! En condiciones normales no varían, algunas, si las ponemos cercas de una singularidad… ¡Puede hasta detenerse! Es el caso de la Gravedad y, también el de la velocidad de la luz que llega al final de su viaje al pasar cerca del agujero negro gigante que la atrae y la engulle. Sin embargo, alguna de estas constantes son esenciales para la vida, y, para no ir más lejos, imaginemos la carga del electrón, o, la masa del protón. Si variaran aunque tan solo fuese una diezmillonésima parte… ¡Los átomos no se podrían formar! Y, entonces… ¡Cómo surgiría la Vida!
Ahora sabemos que el Universo tiene que tener miles de millones de años para que haya transcurrido el tiempo necesario par que los ladrillos de la vida sean fabricados en las estrellas y, la gravitación nos dice que la edad del Universo esta directamente ligada con otros propiedades como la densidad, temperatura, y el brillo del cielo.
Ahora, cuando miramos el Universo, comprendemos, en parte, lo que ahí está presente.
Puesto que el Universo debe expandirse durante miles de millones de años, debe llegar a tener una extensión visible de miles de millones de años luz. Puesto que su temperatura y densidad disminuyen a medida que se expande, necesariamente se hace frío y disperso. Como hemos visto, la densidad del Universo es hoy de poco más que 1 átomo por M3 de espacio. Traducida en una medida de las distancias medias entre estrellas o galaxias, esta densidad tan baja muestra por qué no es sorprendente que otros sistemas estelares estén tan alejados y sea difícil el contacto con extraterrestres. Si existe en el Universo otras formas de vía avanzada, entonces, como nosotros, habrán evolucionado sin ser perturbadas por otros seres de otros mundos hasta alcanzar una fase tecnológica avanzada, entonces, como nosotros, habrán evolucionado sin ser perturbadas por otros seres de otros mundos hasta alcanzar una fase tecnológica avanzada.

La expansión del Universo es precisamente la que ha hecho posible que el alejamiento entre estrellas con sus enormes fuentes de radiación, no incidieran en las células orgánicas que más tarde evolucionarían hasta llegar a nosotras, diez mil millones de años de alejamiento continuado y el enfriamiento que acompaña a dicha expansión, permitieron que, con la temperatura ideal y una radiación baja los seres vivos continuaran su andadura en este planeta minúsculo, situado en la periferia de la galaxia que comparado al conjunto de esta, es solo una cuota de polvo donde unos insignificantes seres laboriosos, curiosos y osados, son conscientes de estar allí y están pretendiendo determinar las leyes, no ya de su mundo o de su galaxia, sino que su osadía ilimitada les lleva a pretender conocer el destino de todo el Universo.
Cuando a solas pienso en todo esto, la verdad es que no me siento nada insignificante y nada humilde ante la inmensidad de los cielos. Las estrellas pueden ser enormes y juntas, formar inmensas galaxias… pero no pueden pensar ni amar; no tienen curiosidad ni en ellas está el poder de ahondar en el porqué de las cosas, nosotros si podemos hacer todo eso y más.
La estructura de los átomos y las moléculas está controlada casi por completo por dos números: la razón entre las masas del electrón y el protón b, que es aproximadamente igual a 1/1.836, y la constante de estructura fina a, que es aproximadamente 1/137. Supongamos que permitimos que estas dos constantes cambien su valor de forma independiente y supongamos también (para hacerlo sencillo) que ninguna otra constante de la Naturaleza cambie. ¿Qué le sucede al mundo si las leyes de la naturaleza siguen siendo las mismas?
Si deducimos las consecuencias pronto encontramos que no hay muchos espacios para maniobrar. Incrementemos b demasiado y no puede haber estructuras moleculares ordenadas porque es el pequeño valor de Beta (aF) el que asegura que los electrones ocupen posiciones bien definidas alrededor de un núcleo atómico y las cargas negativas de los electrones igualan las cargas positivas de los protones haciendo estable el núcleo y el átomo.
Si en lugar de a versión b, jugamos a cambiar la intensidad de la fuerza nuclear fuerte aF, junto con la de a, entonces, a menos que aF > 0,3 a½, los elementos como el carbono no existirían.
No podrían existir químicos orgánicos, no podrían mantenerse unidos. Si aumentamos aF en solo un 4 por 100, aparece un desastre potencial porque ahora puede existir un nuevo núcleo de helio, el helio-2, hecho de 2 protones y ningún neutrón, que permite reacciones nucleares directas y más rápidas que de protón + protón → helio-2.
Las estrellas agotarían rápidamente su combustible y se hundirían en estados degenerados o en agujeros negros. Por el contrario, si aF decreciera en un 10 por 100, el núcleo de deuterio dejaría de estar ligado y se bloquearía el camino a los caminos astrofísicos nucleares hacia los elementos bioquímicos necesarios para la vida.
Hasta donde sabemos, en nuestro sistema solar la vida se desarrolló por primera vez sorprendentemente pronto tras la formación de un entorno terrestre hospitalario. El secreto reside en el tiempo biológico necesario para desarrollar la vida y el tiempo necesario para desarrollar estrellas de segunda generación y siguientes que en novas y supernovas que llegaran a poder cristalizar los materiales complejos necesarios para la vida, tales como el hidrógeno, nitrógeno, oxígeno, carbono… Si miramos por ahí, encontraremos múltiples noticias como estas:

Telescopio Spitzer de la NASA ha detectado los pilares de la vida en el universo distante, aunque en un entorno violento. Ha posado su poderoso ojo infrarrojo en un débil objeto situado a una distancia de 3.200 millones de años luz (recuadro), Spitzer ha observado la presencia de agua y moléculas orgánicas en la galaxia IRAS F00183-7111.
Co,mo podemos ver, amigos míos, la vida, como tantas veces vengo diciendo aquí, pulula por todo el Universo en la inmensa familia galáctica compuesta por más de ciento veinticinco mil millones y, de ese número descomunal, nos podríamos preguntar: ¿Cuántos mundos situados en las zonas habitables de sus estrellas habrá y, de entre todos esos innumerables mundos, cuántos albergaran la vida?
Me gustaría saber cuántas “Tierras” habrá solo en la Vía Láctea
A muchos les cuesta trabajo admitir la presencia de vida en el universo como algo natural, ellos abogan por la inevitabilidad de un universo grande y frío en el que es difícil la aparición de la vida. Yo (como muchos otros), estoy convencido de que la vida es, de lo más natural en el universo y estará presente en miles de millones de planetas que, como la Tierra, tienen las condiciones para ello. Una cosa no se aparta de mi mente, muchas de esas formas de vida, serán como las nuestras aquí en la Tierra y estarán también, basadas en el Carbono. Sin embargo, no niego que puedan existir otras formas de vida diferentes a las terrestres.
Emilio Silvera Vázquez
















 Totales: 86.218.491
Totales: 86.218.491 Conectados: 83
Conectados: 83






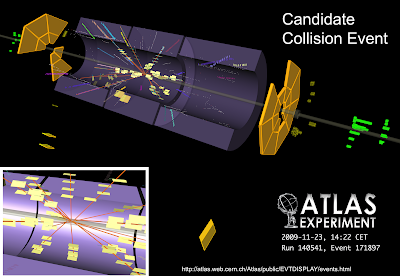
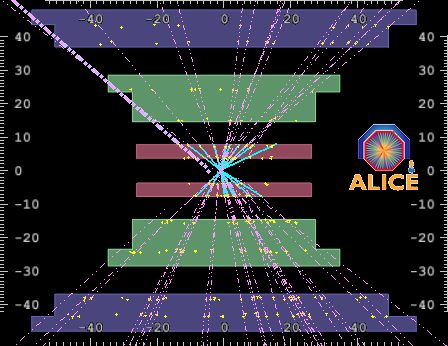























:quality(70)/cloudfront-us-east-1.images.arcpublishing.com/metroworldnews/UJS3PENMVRDPZFBCNO6LQNDAYQ.jpg)





















