¡La Física! Es a veces tan extraña

La Imagen especular (simetría)

La ley conocida como Interacción débil, no cumple con ciertas “leyes de la Física” tales como la conservación de la extrañeza y del isospín, aunque hay otras muchas leyes de conservación que sí respeta.

Los físicos hablan muy a menudo de la conservación de la simetría. Una simetría muy importante, aunque simple, es la “simetría especular” oficialmente llamada “paridad”.

No, esta no es, la imagen especular de un neutrino, de hecho, ellos no tienen imagen especular.

Antes de 1956, siempre se había supuesto que cualquier fenómeno  respetaba las mismas leyes físicas que su imagen especular. En consecuencia uno podría esperar que las partículas o haces de partículas chocan entre ellas de una forma que sea especularmente simétrica, la simetría especular se preservaría.

                                   Los neutrinos siempre nos han dado dolor de cabeza. Su ponemos nuestras manos delante un espejo, ahí las veremos reflejadas. Si de la misma manera, pudiéramos poner dos neutrinos delante del espejo de al lado, eso veríamos: NADA.

El descubrimiento de que muchas partículas no se parecían en nada a sus respectivas imágenes especulares fue realizado por dos físicos chinos, Tsung Dao Lee y Chen Ning Yang, algún tiempo después de haber emigrado a los EE UU. Resultó que la Interacción débil distinguía entre derecha e izquierda. Esto es más claro en el caso del neutrino.

Los neutrinos v_e y v_µ como el fotón, no tienen masa en reposo y, por lo tanto, se mueven siempre a la velocidad de la luz. Los neutrinos también rotan con un espín ½. Si definimos el “polo norte” y el “polo sur” igual que se definen en la Tierra. Los neutrinos son especiales porque siempre tienen el polo sur enfrente de ellos y el polo norte detrás. Nunca se han observados neutrinos para los cuales esto no sea así.

La física sueca Cecilia Jarlskog comparó a los neutrinos con los vampiros porque no tienen imagen especular. Su imagen especular es un imposible físico.

Hace unos días, con ocasión del “hallazgo” del Bosón de Higgs, hablamos aquí del “Mecanismo Higgs”. Pero, ¿es correcto? ¿Nos conducirá hacia una buena teoría? ¿Qué es lo que está permitido y lo que no para describir las partículas elementales y por qué?

El Instituto de Cargèse, en la Isla de Córcega, fue fundado por el físico francés Maurice Lèvy. Desde 1960. Allí, construido en un precioso terreno con una pequeña playa, se realizaban (ahora no se si continúan) escuelas de verano.

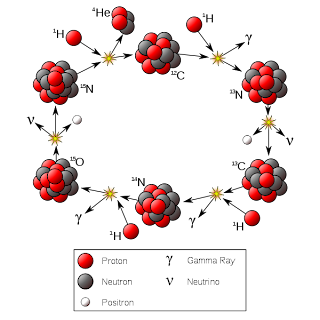
La de 1970 era sobre las interacciones fuertes. Junto con Gell-Mann, Lévy había desarrollado un modelo para la interacción fuerte. Aunque no esperaban que representase toda la verdad, tenía la característica de que se reproducían todas las simetrías de las interacciones fuertes de una forma muy interesante. Pero, debido a que las interacciones son tan fuertes, las partículas no se mueven ni siquiera aproximadamente en línea recta y esto hacía que no se pudiera utilizar el esquema aproximativo habitual, el llamado “desarrollo perturbativo”. A pesar de las dificultades fundamentales que presentaba el modelo con su interminable serie de aproximaciones que no convergían en nada, las discusiones de aquel curso de verano, terminaron dedicándose de forma predominante a intentar extraer de aquel modelo, resultados con algún sentido.

El modelo era interesante. Era un modelo renormalizable en el cual, protones, neutrones y tres clases de piones jugaban un papel muy importante. Pero hacía falta un cuarto acompañante de los piones que se llamó “sigma” (σ). La simetría el modelo requería que los protones “desnudos” y los neutrones no tuvieran masa. Sólo en ese caso se podía entender cómo funcionan las cirrientes sobre las que actúa la interacción débil.

Y, aquí está la parte interesante: se suponía que las partículas sigmas sufrían una condensación Bose y, por lo tanto, aquí también tenemos una “rotura espontánea de simetría”. Los protones y los neutrones, que no tendrían masa en un ambiente simétrico, son entonces frenados por esas partículas sigmas que pueblan el vacío, y adquieren así la masa de la rotura de la simetría. En este sistema se verificaba el teorema de Goldstone, y por lo tanto perdían su masa en reposo.

Aquello no estaba tan mal después de todo. Ya se sabía que los piones eran, con diferencia, los hadrones más ligeros. En la mayoría de las teorías, lo que se tenía que comparar era el cuadrado de las masas de las partículas, y el cuadrado de la masa del pión es aproximadamente catorce veces menor que la masa de la siguiente partícula, el kaón. Una aproximación en la que la masa del pión fuera nula no era, pues, ninguna locura. En una versión mejorado del modelo sigma, podríamos suponer que la masa del pión proviene de una pequeña perturbación. Más tarde, cuando se utilizó el modelo Quarks, se consideró que tanto los piones de Goldstone como la partícula sigma estaban formados por un quark y un anti-quark. La “pertubación” que da la masa al pión resultará ser la pequeña masa de los quarks u y d del interior del hadrón.

 ¡Aquien se le diga que aquí está concentrado todo lo que vemos!

Dos autoridades en el tema de la renormalización, el corenao Benjamin Lee y el alemán Kurt Symanzik, estuvieron en Cargèse, en aquella escuela de verano, para explicar cómo se podía renormalizar en el modelo sigma sin que se perdiera su propiedad más importante, , la rotira espontánea de simetría.

Pero “¿se puede hacer lo mismo si hay un campo de Yang-Mills?”. Gerard ´t Hooft, uno de los alumnos de aquella escuela de verano, le preguntó a Lee y a Symanzik. Ambos le dieron la misma respuesta: “Si yo fuera un estudiante de Veltman le preguntaría a él.” Ellos no habían estuidiado los campos de Yang-Mills, pero a ´t Hooft le pareció que el procedimiento de Lee y Symanzik para el modelo sigma también sería aplicable a cualquier sistema en el que la simetría esté afectada por una condensación de Bose, incluyendo la teoría de Higgs-Kibble. Aquí estaba presente el semillero de una nueva teoría y, ´t Hooft, pensó de inmediato en cómo podía hacerlo crecer.

Esa será otra historia que trataré de contaramos y, de seguro, os interesará.ç

emilio silvera

[?]