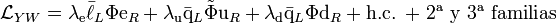Jul
6
¡¡El Bosón de Higgs!!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (5)
Comments (5)
El Acelerador LHC explorará con detalle la alta escala de energía del TeV, con un potencial de descubrimiento de hasta 14 Tera electrón Voltios. Con esta trampa descomunal construida por el hombre, se espera atrapar al esquivo bosón que, según todos los indicios, es el que proporciona la masa a las partículas. Hoy creemos en la existencia de una presencia espectral en el Universo que nos impide conocer la verdadera naturaleza de la materia. Es como si algo quisiera impedirnos ese conocimiento final que nos daría la luz necesaria para que, nuestras mentes, pudieran al fin comprender esa realidad del Universo que, hasta el momento, no hemos sabido vislumbrar, sólo su sombra se nos aparece en algunos experimentos.
Jul
6
La masa de las partículas…El Bosón de Higgs
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (4)
Comments (4)
La puerta de las dimensiones más altas quedó abierta y a los teóricos se les regaló una herramienta maravillosa: el hiperespacio; todo es posible. Hasta el matrimonio de la relatividad general y la mecánica cuántica, allí sí es posible encontrar esa soñada teoría de la gravedad cuántica. Claro que, primero y mientras llega el próximo aceleredor de partículas del futuro, es decir, el que sustituya al LHC, mientras tanto digo, nos hemos dedicado (entre otras cuestiones) a buscar la partícula que, según nos dicen, suministra la masa a las demás, y, según todas las noticias, anuncios y ruedas de prensa, o, entrevistas…¡Ahí está! Veremos ahora que explicaciones se nos dan sobre las consecuencias del hallazgo.

Las singularidades desnudas son una de las más exóticas predicciones de la Teoría de la Relatividad de Einstein. Son bolas de fuego ultra-densas que se piensa que se forman cuando una estrella masiva moribunda, más de cuatro veces más pesada que nuestro Sol, agota su combustible nuclear y colapsa bajo su propio peso. Estas singularidades son llamadas desnudas porque podrían, en principio, ser vistas por los astrónomos.
Así que las teorías se han embarcado a la búsqueda de un objeto audaz: buscan una teoría que describa la simplicidad primigenia que reinaba en el intenso calor del universo en sus primeros tiempos; una teoría carente de parámetros, donde estén presentes todas las respuestas. Todo debe ser contestado a partir de una ecuación básica.
¿Dónde radica el problema?
El problema está en que la única teoría candidata no tiene conexión directa con el mundo de la observación, o no lo tiene todavía si queremos expresarnos con propiedad. La energía necesaria para ello, no la tiene ni el nuevo acelerador de partículas LHC que, siendo el más potente que existe, es aún muy reducido para la prestación de alcanzar la energía de Planck de 1019 GeV.
La verdad es que la teoría que ahora tenemos, el modelo estándar, concuerda de manera exacta con todos los datos a bajas energías y contesta cosas sin sentido a altas energías. ¡Necesitamos algo más avanzado! Y, desde luego, uno de los parámetros del Modelo Estándar, que se metió con calzador, fue ese bosón que suministraba la masa y que era necesario encontrar.

Se ha dicho que la función de la partícula de Higgs es la de dar masa a las partículas que carecen de ella, disfrazando así la verdadera simetría del mundo. Cuando su autor lanzó la idea al mundo, resultó además de nueva, muy extraña. El secreto de todo radica en conseguir la simplicidad: el átomo resultó ser complejo, lleno de esas infinitesimales partículas electromagnéticas que bautizamos con el nombre de electrones. Resultó que tenía un núcleo que contenía, a pesar de ser tan pequeño, casi toda la masa del átomo. El núcleo, tan pequeño, estaba compuesto de otros objetos más pequeños aún; los quarks que estaban instalados en nubes de otras partículas llamadas gluones, y ahora queremos continuar profundizando, sospechando que después de los quarks puede haber algo más.
Bueno, la idea nueva que surgió es que el espacio entero contiene un campo, el campo de Higgs, que impregna el vacío y es el mismo en todas partes, es decir, que si miramos a las estrellas en una noche clara, estamos mirando el campo de Higgs. Las partículas influidas por este campo toman masa. Esto no es por sí mismo destacable, pues las partículas pueden tomar energía de los campos (gauge) de los que hemos comentado: del campo gravitatorio o del electromagnético. Si llevamos un bloque de plomo a lo alto de la Torre Eiffel, el bloque adquirirá energía potencial a causa de la alteración de su posición en el campo gravitatorio de la Tierra. Como E = mc2, ese aumento de la energía potencial equivale a un aumento de la masa, en este caso la masa del sistema Tierra-bloque de plomo. Aquí hemos de añadirle amablemente un poco de complejidad a la venerable ecuación de Einstein: la masa, m, tiene en realidad dos partes; una es la masa en reposo, m0, la que se mide en el laboratorio cuando la partícula está en reposo. La partícula adquiere la otra parte de la masa en virtud de su movimiento (como los protones en el acelerador de partículas, o los muones, que aumentan varias veces su masa cuando son lanzados a velocidades cercanas a c), o en virtud de su energía potencial de campo. Vemos una dinámica similar en los núcleos atómicos. Por ejemplo, si separamos el protón y el neutrón que componen un núcleo de deuterio, la suma de las masas aumenta.

Pero la energía potencial tomada del campo de Higgs difiere en varios aspectos de la acción de los campos familiares. La masa tomada de Higgs es en realidad masa en reposo. De hecho, en la que quizá sea la versión más apasionante de la teoría del campo de Higgs, éste genera toda la masa en reposo. Otra diferencia es que la cantidad de masa que se traga del campo es distinta para las distintas partículas. Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan éstas al campo de Higgs.
La influencia de Higgs en las masas de los quarks y de los leptones nos recuerda el descubrimiento por Pieter Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.
Hasta ahora no tenemos ni idea de qué reglas controlan los incrementos de masa generados por Higgs (de ahí la expectación creada por el nuevo acelerador de partículas LHC), pero el problema es irritante: ¿por qué sólo esas masas - las masas de los W+, W–, Z0, y el up, down, encanto, extraño, top y bottom, así como los leptones – que no forman ningún patrón obvio?

Las masas van desde la del electrón (0’0005 GeV) a la del top, que tiene que ser mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electrodébil (Weinberg-Salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnética y débil. En la unidad hay cuatro partículas mensajeras sin masa – los W+, W–, Z0 y el fotón – que llevan la fuerza electrodébil. Además está el campo de Higgs, y rápidamente, los W y Z absorben la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electrodébil se fragmenta en la débil (débil porque los mensajeros son muy gordos), y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen las teorías. Prefiero la descripción según la cual el Higgs oculta la simetría con su poder dador de masa.
Las masas de los W y Z se predijeron con éxito a partir de los parámetros de la teoría electrodébil, y las relajadas sonrisas de los físicos teóricos nos recuerdan que Hooft y Veltman dejaron sentado que la teoría entera está libre de infinitos.

John Mather, Carlo Rubbia, Martinus Veltman, Gerardus ‘t Hooft at the Lindau Nobel Meetings 2010
Todos los intentos y los esfuerzos por hallar una pista de cuál era el origen de la masa fallaron. Feynman escribió su famosa pregunta: “¿por qué pesa el muón?”. Ahora, por lo menos, tenemos una respuesta parcial, en absoluto completa. Una voz potente y segura nos dice “¡Higgs!”. Durante más de sesenta años los físicos experimentadores se rompieron la cabeza con el origen de la masa, y ahora el campo de Higgs presenta el problema en un contexto nuevo; no se trata sólo del muón. Proporciona, por lo menos, una fuente común para todas las masas. La nueva pregunta feynmaniana podría ser: ¿cómo determina el campo de Higgs la secuencia de masas, aparentemente sin patrón, que da a las partículas de la materia?

La variación de la masa con el estado de movimiento, el cambio de masa con la configuración del sistema y el que algunas partículas (el fotón seguramente, y los neutrinos posiblemente) tengan masa en reposo nula son tres hechos que ponen en entredicho que el concepto de masa sea un atributo fundamental de la materia. Habrá que recordar aquel cálculo de la masa que daba infinito y nunca pudimos resolver; los físicos sólo se deshicieron de él “renormalizándolo”, ese truco matemático que empleam cuando no saben hacerlo bien.
Ese es el problema de trasfondo con el que tenemos que encarar el problema de los quarks, los leptones y los vehículos de las fuerzas, que se diferencian por sus masas. Hace que la historia de Higgs se tenga en pie: la masa no es una propiedad intrínseca de las partículas, sino una propiedad adquirida por la interacción de las partículas y su entorno.
La idea de que la masa no es intrínseca como la carga o el espín resulta aún más plausible por la idílica idea de que todos los quarks y fotones tendrían masa cero. En ese caso, obedecerían a una simetría satisfactoria, la quiral, en la que los espines estarían asociados para siempre con su dirección de movimiento. Pero ese idilio queda oculto por el fenómeno de Higgs.

¿Estarán los campos de Higgs por todas partes, impregnando todo el tejido del espacio tiempo?
Una cosa más; hemos hablado de los bosones gauge y de su espín de una unidad. Hemos comentado también las partículas fermiónicas de la materia (espín de media unidad). ¿Cuál es el pelaje de Higgs? Es un bosón de espín cero. El espín supone una direccionalidad en el espacio, pero el campo de Higgs da masa a los objetos donde quiera que estén y sin direccionalidad. Al Higgs se le llama a veces “bosón escalar” (sin dirección) por esa razón.
La interacción débil, recordaréis, fue inventada por E. Fermi para describir la desintegración radiactiva de los núcleos, que era básicamente un fenómeno de poca energía, y a medida que la teoría de Fermi se desarrolló, llegó a ser muy precisa a la hora de predecir un enorme número de procesos en el dominio de energía de los 100 MeV. Así que ahora, con las nuevas tecnologías y energías del LHC, las esperanzas son enormes para, por fin, encontrar el bosón de Higgs origen de la masa… y algunas cosas más.
Hasta ahora ha sido más fácil saber sobre galaxias lejanas que sobre el Higgs
Hay que responder montones de preguntas: ¿cuáles son las propiedades de las partículas de Higgs? y, lo que es más importante, ¿cuál es su masa? ¿Cómo reconoceremos una si nos la encontramos en una colisión del LHC? ¿Cuántos tipos hay? ¿Genera el Higgs todas las masas o sólo las hace incrementarse? ¿Cómo podemos saber más al respecto? Cómo es su partícula, nos cabe esperar que la veremos ahora después de gastar más de 50.000 millones de euros en los elementos necesarios para ello.
También a los cosmólogos les fascina la idea de Higgs, pues casi se dieron de bruces con la necesidad de tener campos escalares que participasen en el complejo proceso de la expansión del universo, añadiendo pues, un peso más a la carga que ha de soportar el Higgs.
El campo de Higgs, tal como se lo concibe ahora, se puede destruir con una energía grande, o temperaturas altas. Éstas generan fluctuaciones cuánticas que neutralizan el campo de Higgs. Por lo tanto, el cuado que las partículas y la cosmología pintan juntas de un universo primitivo puro y de resplandeciente simetría es demasiado caliente para Higgs. Pero cuando la temperatura cae bajo los 10-5 grados Kelvin o 100 GeV, el Higgs empieza a actuar y hace su generación de masas. Así, por ejemplo, antes del Higgs teníamos unos W, Z y fotones sin masa y la fuerza electrodébil unificada.

El universo se expande y se enfría, y entonces viene el Higgs (que “engorda” los W y Z, y por alguna razón ignora el fotón) y de ello resulta que la simetría electrodébil se rompe.
Tenemos entonces una interacción débil, transportada por los vehículos de la fuerza W+, W–, Z0, y por otra parte una interacción electromagnética, llevada por los fotones. Es como si para algunas partículas del campo de Higgs fuera una especie de aceite pesado a través del que se moviera con dificultad y que les hiciera parecer que tienen mucha masa. Para otras partículas, el Higgs es como el agua, y para otras, los fotones y quizá los neutrinos, es invisible.
De todas formas, es tanta la ignorancia que tenemos sobre el origen de la masa que nos agarramos como a un clavo ardiendo, en este caso, a la partícula de Higgs, que algunos han llegado a llamar “la partícula divina”.
¡Ya veremos en qué termina todo esto!

Aquí Peter Higgs quiso visitar el ingenio que, hipotéticamente, encontrará “su partícula”
Peter Higgs, de la Universidad de Edimburgo, introdujo la idea en la física de partículas. La utilizaron los teóricos Steven Weinberg y Abdus Salam, que trabajaban por separado, para comprender cómo se convertía la unificada y simétrica fuerza electrodébil, transmitida por una feliz familia de cuatro partículas mensajeras de masa nula, en dos fuerzas muy diferentes: la QED con un fotón carente de masa y la interacción débil con sus W+, W– y Z0 de masa grande. Weinberg y Salam se apoyaron en los trabajos previos de Sheldon Glashow, quien, tras los pasos de Julian Schwinger, sabía sólo que había una teoría electrodébil unificada, coherente, pero no unió todos los detalles. Y estaban Jeffrey Goldstone y Martinus Veltman y Gerard’t Hooft. También hay otros a los que habría que mencionar, pero lo que siempre pasa, quedan en el olvido de manera injusta. Además, ¿cuántos teóricos hacen falta para encender una bombilla? La verdad es que, casi siempre, han hecho falta muchos. Recordemos el largo recorrido de los múltiples detalles sueltos y físicos que prepararon el terreno para que llegara Einstein y pudiera, uniéndolo todo, exponer su teoría relativista.
Sobre la idea de Peter Higgs, Veltman, uno de sus arquitectos, dice que es una alfombra bajo la que barremos nuestra ignorancia. Glashow es menos amable y lo llamó retrete donde echamos las incoherencias de nuestras teorías actuales. La objeción principal: que no tenemos la menor prueba experimental. Ahora, por fin, la tendremos con el LHC. El modelo estándar es lo bastante fuerte para decirnos que la partícula de Higgs de menor masa (podría haber muchas) debe “pesar” menor de 1 TeV, ¿por qué?; si tiene más de 1 TeV el modelo estándar se vuelve incoherente y tenemos la crisis de la unitariedad.
Después de todo esto, llego a la conclusión de que el campo de Higgs, el modelo estándar y nuestra idea de donde surgió el universo dependen de que se encuentre el bosón de Higgs. Y ahora, por fin, tenemos un acelerador con la energía necesaria para que nos la muestre, y que con su potencia pueda crear para nosotros una partícula que pese nada menos que 1 TeV.
Las últimas noticias sobre el tema me hacen reponer de nuevo este trabajo que está relacionado con el Campo de Higgs y su Bosón.
emilio silvera
Jul
5
A vueltas con el Bosón de Higgs
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (12)
Comments (12)
ALVARO DE RúJULA
CSIC, UAM, CERN y Boston University
El bosón “de Higgs”
El Large Hadron Collider del CERN (LHC) es, entre otras cosas, una máquina de sacudir el vacío, ya que su principal objetivo es encontrar el bosón de Higgs o demostrar que no existe. En general, demostrar que algo no existe es imposible. El éxito del experimento de Michelson y Morley fue su fracaso. Asimismo, el máximo éxito del LHC consistiría en demostrar que no existe el Higgs. Esto nos situaría en una tesitura científica prerrevolucionaria, quizás análoga a la que tuvo lugar en el albor del siglo XX.
Hace 124 años Michelson y Morley publicaron su crucial experimento. Se trataba de medir el movimiento de la Tierra con relación al éter, la interpretación newtoniana del vacío como la trama del espacio absoluto. Mucho después aún estamos intentando entender el vacío, con medios como el tupido entramado de aceleradores del CERN (Figura 1) y varios de sus detectores, como CMS y ATLAS (Foto 1) DESTACADOSGlosario de materia y energíaPerfil: Álvaro de Rújulaque ya no son experimentos de mesa. El fracaso de Michelson y Morley acabaría apuntalando la visión einsteniana: el vacío no es un escenario en el que las cosas están o se mueven. Al contrario, esas mismas cosas configuran el espacio-tiempo en el que están.
Las “teorías cuánticas relativistas” predictivas –llamadas teorías de campos “renormalizables”– tienen la particularidad de que, en ellas, lo que no está prohibido es obligatorio, como en las dictaduras. Para que la teoría prohíba un proceso no observado es necesario que una simetría de la teoría lo haga. De otro modo las correcciones “cuánticas” (en potencias sucesivas de la constante de Plank) lo generan, con una amplitud impredecible, para más inri.
El modelo estándar es una tal teoría, en la que se basa nuestro entendimiento de las partículas elementales y sus interacciones. Ab initio, una de sus simetrías, misteriosamente llamada “de calibre (gauge)” prohíbe que las partículas tengan las masas no nulas que caracterizan a su gran mayoría; solo fotones y “gluones” tienen masas cero. Romper la simetría a mano no funciona, El modelo estándar es una tal teoría, en la que se basa nuestro entendimiento de las partículas elementales y sus interaccionesla teoría pierde su capacidad predictiva, adquiriendo infinitos parámetros arbitrarios. En nuestro inescrutable lenguaje litúrgico, la teoría deja de ser renormalizable.
Para salir del atolladero es necesario que la rotura de la simetría sea “espontánea”. Un perdigón en el fondo de una probeta vertical está en una posición simétrica (en el eje) y estable (en el fondo). Calentemos la probeta y deformémosla hasta que su fondo se parezca al de una botella. Si realizamos la operación con inconmensurable destreza, la bola se quedará en el eje, posición simétrica, pero inestable. De otro modo se caerá en una dirección cualquiera; la simetría original se ha roto espontáneamente: hay una dirección preferente, que pudiera haber sido cualquier otra. Como en un ferroimán “de Heisenberg” en el que los espines de los átomos interaccionan entre ellos y, por debajo de una temperatura crítica, se alinean espontáneamente. La teoría tiene una simetría (todas las direcciones son equivalentes) aunque sus soluciones de mínima energía (el imán frío) apunten en una dirección espontáneamente generada.
El mecanismo de Higgs
La energía gravitacional o la de interacción entre espines del párrafo anterior se describen como “potenciales” de interacción. El modelo estándar incluye el potencial de un hipotético campo escalar (de espín cero): el campo “de Higgs”. En el estado de mínima energía (¡el vacío!), el campo rompe la simetría gauge y una de sus componentes, que es neutra, adquiere un valor constante no nulo (su valor en el vacío). La teoría “rota” tiene pues un vacío que no está vacío, sino permeado por una “substancia”: un campo constante. A diferencia del viejo éter, este vacío es invariante relativista (es el mismo para un observador que para otros en movimiento respecto a él) y hasta invariante general-relativista (el valor del campo en el vacío no se diluye, aunque el universo se expanda).
Una vez añadido el campo escalar, todo lo del párrafo anterior “le pasa” al modelo estándar, pero también –inevitablemente– le pasan otras cosas. Las partículas de espín ½ (como el electrón y los quarks) adquieren masa, puesto que su interacción con el vacío –que ya no lo está– tiene ahora la forma (única e inevitable) de un “término” de masa. Algo aún más sorprendente le pasa a los “bosones intermediarios” (W+ , W- y Z0), las partículas de espín 1 mediadoras de las interacciones débiles, responsables, por ejemplo, de la radiactividad natural. De entrada tienen masa nula y, como Siguiendo una más antigua tradición, opino que, el bosón de Higgs debería de llamarse el “kenonón”, del griego kenon, “vacío”el fotón, dos estados de polarización. Una vez que la simetría de gauge está rota, adquieren masa, lo cual requiere un tercer estado de polarización o “grado de libertad”. Este grado lo heredan de las otras tres componentes del campo de Higgs, que de entrada tiene cuatro: dos eléctricamente cargadas y dos neutras, solo una de las cuales sobrevive como el campo que “llena” el vacío.
Hay que admitir que todo lo anterior suena a cuento, pero no lo es: el modelo estándar describe lo observado con precisión impresionante. Su parte mejor comprobada es la “electrodinámica cuántica”: la interacción del fotón con las partículas cargadas (la carga eléctrica es la capacidad de emitir o absorber fotones). Puede uno predecir, por ejemplo, el cociente giro-magnético del electrón: la intensidad con la que se comporta como un imán puntual. Observación y teoría son crecientemente precisas y coinciden hoy en día en 14 (¡catorce!) cifras significativas. Las interacciones fuertes (entre quarks) y débiles no están medidas con precisión tan espeluznante, pero sí la suficiente como para indicarnos que vamos por buen camino. El cociente de masas M(W)/M(Z), siendo M la masa y W y Z los bosones intermediarios, es el predicho por el “mecanismo” de Higgs que he esbozado.

Foto 1. Una vista parcial de ATLAS, uno de los detectores del LHC, en su subterráneo punto de colisión, durante su ensamblaje. Atlas mide 25 m de alto y 46 de largo y pesa 7.000 toneladas, casi como la torre Eiffel. El detector incluye 3.000 km de cables y tiene 100 millones de canales electrónicos, además de incontables componentes de variadas tecnologías de punta. Fuente: CERN.
El bosón de Higgs
A todo este edificio estándar le falta una constatación: el descubrimiento del “bosón de Higgs”. Ya va siendo hora de recordar que un bosón es una partícula de espín entero, como el fotón, cuyo espín es la unidad. Un fermión (como el electrón) es una partícula de espín semi-entero (½ en este caso). Los fermiones son asociales: solo cabe uno en un estado cuántico determinado. Los bosones, como los hinchas, son lo contrario: añadirlos sucesivamente en el mismo estado cuesta cada vez menos energía.
Al sacudir una substancia cualquiera, vibra. Las vibraciones de campos electromagnéticos, por ejemplo, son la luz. A un nivel elemental, las vibraciones son cuantos (o partículas): fotones este caso. Si existe una substancia, el campo de Higgs que permea el vacío, la podríamos también “sacudir” con energía suficiente como para crear sus correspondientes cuantos (bosones de Higgs) de masa aún desconocida.
En buena liza, el bosón de Higgs debería llamarse de Peter Higgs, François Englert y Robert Brout y quizás de algunos más. Los físicos de partículas hemos perdido con este bosón la ocasión de darle un mejor nombre; algunos intentos que no citaré son patéticos. La tradición es bautizar a las partículas con nombres absurdos, como “quarks” y a las teorías con nombres engañosos y rimbombantes, como “cromodinámica cuántica”. Siguiendo una más antigua tradición, opino que, el bosón de Higgs debería de llamarse el “kenonón”, del griego kenon, “vacío”. Sin decencia poética, lo solemos llamar “el Higgs”. Como quién dijese “el Litri”.
El LHC
El Large Hadron Collider (LHC) del CERN es un colisionador de hadrones: partículas constituidas por quarks o por quarks y antiquarks, cuyas interacciones “cromodinámicas” están mediadas por gluones y son fuertes. Protones, neutrones y los núcleos de los átomos son hadrones, P=(uud), N=(udd), siendo u y d los quarks “up” y “down” (como de costumbre, ni up ni down tienen el sentido que debería ser habitual).
En el LHC se hacen colisionar desde protones hasta núcleos de plomo. Por ahora la energía de los protones es de 3.5 teraelectronvoltios (TeV), unas 3.740 veces su energía en reposo, mc2. Lo suficiente como para batir por un factor 7 el record anterior, del colisionador en Fermilab, también cerca de Ginebra, pero Geneva, Illinois. La luminosidad de un colisionador (veces la sección eficaz del proceso de colisión) es la cadencia de las colisiones. El LHC progresa rápidamente hacia su luminosidad de diseño, pero de momento funciona solo a la mitad de su energía máxima.
La máquina consta de dos anillos que guían y aceleran partículas en direcciones contrarias y las hacen colisionar en cuatro puntos, véase la Figura 1. Los protones le llegan al LHC parcialmente acelerados en una tortuosa serie de aceleradores “antiguos”. En los puntos de colisión del LHC hay un par de experimentos pequeños (TOTEM y LHCf) y cuatro medianos: ATLAS (Foto 1), CMS, LHCb y ALICE. No caeré en el error, ya inevitable en el caso del LHC, de llamarlos “grandes”. En realidad estamos siempre proyectando otros mayores.
A la caza del Higgs
La mayoría de las partículas que existen son inestables y, a primera vista, inútiles. Para estudiarlas, primero hay que crearlas. Para ello es necesario producir colisiones de una energía (en el “centro de masa”) superior a la energía en reposo de la partícula en cuestión. A los “particuleros” nos resulta más fácil decir estas cosas, puesto que no distinguimos entre energía y masa. Por ejemplo, en la fórmula
E = mc² / √(1 – v² / c²), ponemos la velocidad de la luz c=1, una simple elección de unidades. Si medimos tiempos en nanosegundos y distancias en unidades de “mi pié izquierdo”, c=1 puesto que dicho pié (de unos 30 cm) mide precisamente (por definición) lo que la luz en el vacío recorre en un nanosegundo. Por cierto, la consabida E = mc² es falsa. Es válida para un objeto en reposo, en cuyo caso es casi tautológica.
El LHC es, entre otras cosas, un MSV (Máquina de Sacudir el Vacío) ya que su principal objetivo es encontrar el bosón de Higgs o demostrar que no existe. En general, demostrar que algo no existe es imposible. Este caso es una excepción. Con un Higgs de masa superior a 1 TeV, el modelo estándar violaría la “unitariedad”: predeciría absurdamente procesos con probabilidad superior al 100%. El LHC alcanza para fabricar objetos de masa 1 TeV, y si no encuentra el Higgs, después de algunos años buscándolo, es que no existe. O tiene propiedades significativamente distintas a las previstas, en cuyo caso no es “el” Higgs.
El proceso más probable de producción del Higgs es el de la Figura 2. Curiosamente tendría lugar a través de un “triángulo virtual” de quarks “top”. La razón es que este quark es el más masivo y el Higgs se “acopla” a las partículas proporcionalmente a su masa: así es como el campo de Higgs en el vacío genera las masas.
El proceso de desintegración del Higgs que mejor permitiría medir sus propiedades –y saber si su identidad es la que le atribuimos– está también esbozado en la Figura 2. La razón es que electrones o sus “réplicas” inestables de mayor masa, los muones, son las partículas cuya energía y dirección pueden medirse con mayor precisión, permitiendo determinar bien el espín y “acoplamientos” del Higgs.
Colofón
Ha renacido como venganza póstuma la vieja idea de Einstein que él repudió al enterarse de que el universo no era estático: la “constante cosmológica (L)”, el único ente estático que puede ejercer una repulsión gravitacional. Einstein la introdujo para estabilizar el universo artificialmente contra la atracción gravitacional entre las galaxias, que lo colapsaría. El universo está en expansión acelerada. Esto implica que L no es nula, como opinábamos hasta hace poco sin saber porqué. Todos los datos concuerdan con la posibilidad de que dicha L sea la responsable de la aceleración observada.
En terminología actual, L es la densidad de energía del vacío. Entendemos el modelo estándar lo suficiente como para estimar cuánto el campo de Higgs contribuye a la diferencia de potencial –o densidad de energía– entre el falso vacío inestable (la bola en lo alto del trasero de la botella) y el verdadero vacío (la bola abajo). La gravedad responde directamente a la densidad de energía (e impulso) y no, como las demás fuerzas, solo a diferencias de potencial. La contribución del campo de Higgs a la constante cosmológica debería ser del orden de la diferencia de potencial entre vacíos falso y verdadero. Pero el resultado de esta estimación es unos 54 (¡cincuenta y cuatro!) órdenes de magnitud superior a las observaciones cosmológicas. Tiene su mérito incurrir en tamaña contradicción.
Quizás comprendamos por qué las partículas tienen masa, pero no por qué tienen los valores de masa que tienen. Hemos visto otros defectos de nuestro entendimiento del vacío y de un campo que supuestamente lo permea. Queremos saber más, de ahí el encono en buscar el Higgs, o algo que se le parezca. O que no se le parezca.
El éxito del experimento de Michelson y Morley fue su fracaso. Asimismo, el máximo éxito del LHC consistiría en demostrar que no existe el Higgs. Esto nos situaría en una tesitura científica prerrevolucionaria, quizás análoga a la que tuvo lugar en el albor del siglo XX. Cedo al amable lector el reto de convencer a las autoridades competentes (con su siempre superior criterio) de que el mayor descubrimiento sería, en este caso, no encontrar lo que uno busca.
Apéndice: una labor global
En el CERN trabajan unos 2.300 empleados, 20 de ellos, físicos teóricos con contratos de tres o más años. Hay también unos 7.000 “usuarios”, estudiantes, científicos, ingenieros y técnicos de unos 70 países, muchos de ellos, como Suiza y España, multilingües. Un aguerrido lingüista podría detectar centenares de idiomas en las babélicas cafeterías del CERN, o dialectos de países –como Italia o Francia– en los que no son armas el idioma y la poesía. En total, en los experimentos del LHC, trabajan unos 330 españoles.
El presupuesto del CERN, pagado por los veintipocos países miembros proporcionalmente a su producto interno bruto (con un tope de 20% del presupuesto para Alemania), es de unos mil millones de francos suizos al año, a los que España contribuye aproximadamente con un 7%. Esto significa que los españoles contribuimos cada uno a razón de un euro al año.
Es difícil sobrestimar el impacto de la investigación fundamental en la Economía, Tecnología o Medicina a plazo fijo, relacionado frecuentemente con las próximas elecciones. Me limitaré a dar el ejemplo consuetudinario de la flauta que sonó, aunque no por casualidad. El Hipertext Transfer Protocol (el misterioso “http” de las páginas web) fue inventado en el CERN por Tim Berners-Lee. Es la base de la explosión del uso de Internet. Berners-Lee, con el beneplácito inicialmente escéptico y la indispensable libertad académica que le otorgaban sus jefes, se propuso encontrar un lenguaje universal con el que grupos de físicos pudieran intercambiar datos, independientemente del tipo de ordenadores que empleasen. Y dio en un clavo sin fronteras, como el propio CERN.
Glosario de materia y energía
son idénticas a su antipartícula.
Antiquark. Antipartícula que corresponde a un quark. El número de tipos de quarks y antiquarks en la materia es el mismo. Se representan con los mismos símbolos que aquellos, pero con una barra encima de la letra correspondiente, por ejemplo, si un quark se representa con u, un antiquark se escribe u.
Bosón de Higgs. Partícula elemental que queda por descubrir para cerrar con éxito el denominado modelo estándar de la Física de partículas. El hallazgo de su existencia es clave para entender la forma en que las demás partículas adquieren masa.
Bosón. Uno de los dos tipos básicos de partículas elementales, de espín entero (el otro tipo son los fermiones, de espín seminetero).
Brana. Una palabra inglesa que quiere decir membrana multidimensional, esto es un subespacio de un espacio más grande. Por ejemplo, una 2-brana es una membrana ordinaria (una superficie de dos dimensiones).
Campo gauge. Los campos gauge son generalizaciones del electromagnetismo, y describen las interacciones fundamentales. El campo de color(cromodinámica cuántica) cuyas partículas asociadas son los ocho gluones, describe las interacciones fuertes, mientras que el campo electrodébil (cuyas partículas asociadas son los bosones W^+, W^-, Z^0 y el fotón) describe las interacciones electromagnéticas y las débiles.
Campo. Ente básico que describe las partículas elementales y sus interacciones. El campo gravitatorio hace caer la manzana y orbitar la luna. El campo electromágnetico media las fuerzas correspondientes. Los campos “cuánticos” tienen un comportamiento “dual”: sus vibraciones son partículas (fotones) y ondas. Un campo cuántico relativista es uno que satisface los postulados de las correspondientes –y altamente comprobadas– teorías.
Carga de color. Propiedad de los quarks y los gluones que cuantifica su capacidad de emitir o absorber gluones, mediadores de la interacción fuerte en el contexto de la cromodinámica cuántica (QCD).
Constante de acoplamiento. Cantidad que determina la amplitud de una interacción. La carga eléctrica es un ejemplo, en el caso de la interacción de fotones con partículas cargadas.
Constante de Plank. Relación entre la cantidad de energía y de frecuencia asociadas a una partícula. Desempeña un papel central en la Mecánica cuántica. Si la anulamos a mano, obtenemos la Mecánica clásica.
Corrección cuántica. Hay cantidades que son intrínsecamente cuánticas, como el espín, que no tiene análogo clásico. Pero en otros casos, al calcular el valor de un observable, hay una contribución clásica, a la que hay que añadirle una corrección cuántica proporcional a la constante de Planck.
Cromodinámica cuántica. (QCD). Teoría cuántica de campos que describe una de las fuerzas fundamentales, esto es, la interacción fuerte que es la responsable de las fuerzas entre quarks.
Cilatón. Hipotética partícula que aparece en la teoría de cuerdas.
Espín. Es un efecto cuántico que implica que existe un momento angular residual incluso en el sistema de referencia en el que la partícula está en reposo. Si el espín es entero, (0,1,2) se dice que la partícula es un bosón, y si es semientero (1/2,3/2), se dice que es un fermión. El principio de exclusión de Pauli, que afirma que dos fermiones idénticos no pueden estar en el mismo nivel cuántico, es el que explica la estructura de la tabla periódica de Mendeleev.
Fonón. Cuasipartícula o modo cuantizado de vibración que tiene lugar en redes cristalinas, como la red atómica de un sólido.
Fotón. Partícula elemental responsable de las manifestaciones cuánticas del fenómeno electromagnético. Es la partícula que media las fuerzas eléctricas y magnéticas y que constituye todas las formas de radiación electromagnética, incluyendo los rayos gamma, los rayos X, la luz ultravioleta, la luz visible, la luz infrarroja, las microondas y las ondas de radio.
Gluón. Bosón portador de la interacción “cromodinámica” o fuerte, una de las cuatro fuerzas fundamentales. No posee masa ni carga eléctrica, pero sí carga de color, por lo que además de transmitir la interacción fuerte también la sufre.
Gravitón. Partícula elemental hipotética de tipo bosónico que sería la transmisora de la interacción gravitatoria en la mayoría de los modelos
de gravedad cuántica.
Leptón. Fermión fundamental sin carga hadrónica o de color. Existen seis leptones y sus correspondientes antipartículas: el electrón, el muón, el tau y tres neutrinos asociados a cada uno de ellos.
Modelo estándar de la Física de partículas. Teoría que describe las relaciones e interacciones conocidas entre las partículas elementales que componen la materia. Sin embargo, el modelo estándar no alcanza a ser una teoría completa de las interacciones fundamentales, puesto que no incluye una teoría cuántica de la gravitación, la cuarta interacción fundamental conocida.
Principio de incertidumbre de Heisenberg. La naturaleza dual de los “campos” que describen los aspectos “onda” y “partícula” de objetos tales como la radiación electromagnetica, impone restricciones en la capacidad para determinar al mismo tiempo su posición y su impulso, u otros pares de observables “complementarios”.
Quarks. Partículas fundamentales con carga “fuerte” y carga eléctrica fraccionaria. Dos de ellos (up y down) son los constituyentes de protones y neutrones.
Simetría. Equivalencia de varias posibilidades. En un espacio vacio, todas las direcciones son equivalentes. Un cubo perfecto tiene una simetría menor (solo giros de 90 grados lo dejan como estaba). Algunas simetrías son “internas” (en “espacios” definidos matemáticamente). Por ejemplo el quark up y el quark down son idénticos, si despreciamos sus diferentes masas y cargas eléctricas. “Apuntan” up o down en un espacio “interno”.
Supersimetría. Simetría hipotética que relaciona las propiedades de los bosones y los fermiones. Aunque no se ha verificado experimentalmente que se trate de una simetría de la naturaleza, constituye una parte fundamental de muchos modelos teóricos, incluyendo la teoría de supercuerdas. La supersimetría también es conocida por el acrónimo inglés SUSY.
Teoría de cuerdas. Modelo de la Física que supone que las partículas no son un “punto” sin estructura interna y de dimensión cero, sino una cuerda minúscula que vibra en un espacio-tiempo de más de cuatro dimensiones. Esta teoría, ampliada con otras como la de las supercuerdas o la Teoría M, pretende alejarse de la concepción del punto-partícula.
Teoría M. Hipotética teoría que, partiendo de la teoría de cuerdas, pretende convertirse en una “teoría del todo” capaz de unificar las cuatro fuerzas fundamentales de la naturaleza. Imaginada por Edward Witten, combina las cinco teorías de supercuerdas y supergravedad en once dimensiones.
Perfil: Álvaro de Rújula

Doctor en Física Teórica por la Universidad Complutense de Madrid, de la que fue profesor. Impartió clases en el Institut des Hautes Études Scientifiques (IHES) de París y en la Universidad de Harvard. Forma parte, desde 1977, del equipo del Centro Europeo de Investigaciones Nucleares (CERN) y es docente de la Universidad de Boston, desde 1985. Es colaborador del premio Nobel de Física Sheldon Glashow.
Miembro electo de la Academia Europea, desde 1991; del Instituto de Física Teórica UAM/CSIC y del Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas (CIEMAT), desde 2009.
Como físico teórico, de Rújula se ha ocupado de diversos temas clave de esta disciplina, tanto de asuntos que tienen que ver con la estructura interna del átomo como de cuestiones relacionadas con la Cosmología y la Astrofísica. Es uno de los principales investigadores del equipo del CERN que ha puesto en marcha el Gran Colisionador de Hadrones ( LHC).
Jul
5
¡La máquina de Higgs-Kibble! El Vacío superconductor
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)

2010 APS J.J. Sakurai Premio – Kibble, Guralnik, Hagen, Englert, Brout.
Investigación experimental
Hasta la fecha, el bosón de Higgs no ha sido observado experimentalmente, a pesar de los esfuerzos de los grandes laboratorios de investigación como el CERN o el Fermilab. La no observación de pruebas claras permite estimar un valor mínimo experimental de masa 114.4 GeV para el bosón de Higgs del modelo estándar, con un nivel de confianza del 95%.[6] Experimentalmente se ha registrado un pequeño número de eventos no concluyentes en el colisionador LEP en el CERN. Éstos han podido ser interpretados como resultados de los bosones de Higgs, pero la evidencia no es concluyente.[7] Se espera que el Gran Colisionador de Hadrones, ya construido en el CERN, pueda confirmar o desmentir la existencia de este bosón. El anillo de 27 km de circunferencia (llamado Large Hadron Collider) fue encendido el 10 de septiembre de 2008, como estaba previsto, pero un fallo en el sistema de enfriamiento que debe mantener los imanes a una temperatura aproximada de -271,3 °C detuvo el experimento, hasta el 20 de noviembre del 2009, fecha en que volvió a ser encendido, desde 450 GeV a 2.23 TeV. Pero fue apagado para realizar ajustes, y el 30 de marzo volvió a ser encendido, aunque a potencia de 7 TeV. Eso si, no será hasta 2016 cuando funcione a pleno rendimiento.
La búsqueda del bosón de Higgs es también el objetivo de ciertos experimentos del Tevatrón en el Fermilab
Alternativas al mecanismo de Higgs para la ruptura espontánea de simetría electrodébil
Desde los años en los que fue propuesto el bosón de Higgs, han existido muchos mecanismos alternativos. Todas las otras alternativas usan una dinámica que interactúa fuertemente para producir un valor esperado del vacío que rompa la simetría electrodébil. Una lista parcial de esos mecanismos alternativos es:
Technicolor es la clase de modelo que intenta imitar la dinámica de la fuerza fuerte como camino para romper la simetría electrodébil.
El modelo de Abbott-Farhi de composición de los bosones de vectores W y Z.
Campo de Higgs
El Campo de Higgs es un campo cuántico, que, de acuerdo con una hipótesis del modelo estándar de física de partículas expuesta por el físico Peter Higgs, permearía el universo entero, y cuyo efecto sería que las partículas se comportaran como dotadas de masa, debido a la interacción asociada de partículas elementales, con el bosón de Higgs, cuya existencia aún no ha sido probada directamente y que por la interacción consigo mismo también “adquiriría” masa. Se espera que el Gran Colisionador de Hadrones sirva para probar las hipótesis de Higgs.
Mecanismo de Higgs

El mecanismo de Higgs, ideado por Peter Higgs entre otros, es uno de los mecanismos posibles para producir la ruptura espontánea de simetría electrodébil en una Teoría Gauge invariante. Permitió establecer, la unificación entre la teoría electromagnética y la teoría nuclear débil, que se denominó Teoría del campo unificado dando premio Nobel en año 1979 a Steven Weinberg, Sheldon Lee Glashow y Abdus Salam
Este mecanismo también es conocido como mecanismo de Brout–Englert–Higgs, mecanismo de Higgs–Brout–Englert–Guralnik–Hagen–Kibble, o mecanismo de Anderson–Higgs. En 1964, fue inicialmente propuesto por Robert Brout y François Englert, e independientemente por Peter Higgs y por Gerald Guralnik, C. R. Hagen, y Tom Kibble.Fue inspirado en la Teoría BCS de rompimiento de simetría en superconductividad basado en Teoría Ginzburg-Landau, los trabajos de la estructura del vacío de Yoichiro Nambu, y las ideas de Philip Anderson según las cuales la superconductividad podía ser relevante en la relatividad, el electromagnetismo y otros fenomenos clásicos. El nombre de mecanismo de Higgs fue dado por Gerardus ‘t Hooft en 1971. Los tres artículos originales de Guralnik, Hagen, Kibble, Higgs, Brout, y Englert en donde se propone este mecanismo fueron reconocidos como fundamentales en la celebración del aniversario 50 de la revista Physical Review Letters
Campos y partículas
La segunda mitad del siglo XX fue un tiempo de descubrimiento de nuevas partículas elementales, nuevas fuerzas y, sobre todo, nuevos campos. El espacio puede llenarse con una amplia variedad de influencias invisibles que tienen todo tipo de efectos sobre la materia ordinaria. De todos los nuevos campos que se descubrieron, el que tiene más que enseñarnos sobre el paisaje es el campo de Higgs. Existe una relación general entre partículas y campos. Por cada tipo de partícula de la naturaleza hay un campo y por cada tipo de campo hay una partícula. Así campos y partículas llevan el mismo nombre. El campo electromagnético podría denominarse campo de fotones. El electrón tiene un campo, también lo tienen el quark, el gluón y cada miembro del reparto de personajes del modelo Standard, incluida la partícula de Higgs.
El campo de Higgs

En la concepción del Modelo estándar de física de partículas, el boson de Higgs así como otros bosones (encontrados ya experimentalmente) y ligados en esta teoría, se interpretan desde el Bosón de Goldstone donde cada parte del rompimiento de simetría genera un campo, para el cual los elementos que viven en este campo son sus respectivos bosones. Existen teorías creadas a partir del miedo de la no existencia del boson de Higgs donde no es necesaria su aparición. El campo de Higgs es el ente matemático donde existe, su interpretación con la teoría es el producto de él con los otros campos que sale por el mecanismo de ruptura, este producto nos da el acople y la interacción de él, con esta interacción con los otros campos legamos la caracteristica de generador de masa.
Me resistía pero…Formulación matemática
Introducimos un campo adicional ? que rompa la simetría SU(2)L × U(1)Y ? U(1)em. Debido a las condiciones que se exigen a la teoría será un doblete (de SU(2)L) de campos escalares complejos (doblete de Higgs):
Dobletes de Higgs

El número total de entradas (número dimensional del vector) de Higgs no está determinado por la teoría y podría ser cualquiera. No obstante la versión mínima del SM posee uno solo de estos dobletes.
El sistema vendrá entonces descrito por un Lagrangiano de la forma:
tal que:
donde V(phi) es el potencial renormalizable (y por tanto que mantiene la invarianza gauge) más sencillo. Para que se produzca ruptura espontánea de simetría es necesario que el valor esperado del campo de Higgs en el vacío sea no nulo. Para lambda mayor que 0, si mu 2 menor que 0, el potencial posee infinitas soluciones no nulas (ver figura 1), en las cuales sólo la norma del campo de Higgs está definida:
Estado fundamental
El estado fundamental está, por consiguiente, degenerado y no respeta la simetría del grupo SU(2)L × U(1)Y. Sin embargo, sí conserva la simetría del grupo U(1)em. El valor de cup ? indica la escala de energía a la que se produce la ruptura de la simetría electrodébil. La ruptura SU(2)L × U(1)Y Phi U(1)em se produce cuando se selecciona un estado del vacío concreto. La elección habitual es aquella que hace que Phi 3 sea no nulo:
Espectro de partículas
El espectro de partículas físicas resultantes se construye realizando pequeñas oscilaciones en torno al vacío, que pueden ser parametrizadas en la forma:
donde el vector 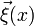 y el escalar h(x) son campos pequeños correspondientes a los cuatro grados de libertad reales del campo . Los tres campos
y el escalar h(x) son campos pequeños correspondientes a los cuatro grados de libertad reales del campo . Los tres campos 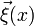 son los bosones de Goldstone, de masa nula, que aparecen cuando una simetría continua es rota por el estado fundamental (teorema de Goldstone).
son los bosones de Goldstone, de masa nula, que aparecen cuando una simetría continua es rota por el estado fundamental (teorema de Goldstone).
En este punto aún tenemos 4 bosones gauge (Wi?(x) y B?(x)) y 4 escalares (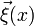 y h(x)), todos ellos sin masa, lo que equivale a 12 grados de libertad (Conviene notar que un bosón vectorial de masa nula posee dos grados de libertad, mientras que un bosón vectorial masivo adquiere un nuevo grado de libertad debido a la posibilidad de tener polarización longitudinal: 12 = 4[bosones vectoriales sin masa] × 2 + 4[escalares sin masa]). P. W. Higgs fue el primero en darse cuenta de que el teorema de Goldstone no es aplicable a teorías gauge, o al menos puede ser soslayado mediante una conveniente selección de la representación. Así, basta con escoger una transformación:
y h(x)), todos ellos sin masa, lo que equivale a 12 grados de libertad (Conviene notar que un bosón vectorial de masa nula posee dos grados de libertad, mientras que un bosón vectorial masivo adquiere un nuevo grado de libertad debido a la posibilidad de tener polarización longitudinal: 12 = 4[bosones vectoriales sin masa] × 2 + 4[escalares sin masa]). P. W. Higgs fue el primero en darse cuenta de que el teorema de Goldstone no es aplicable a teorías gauge, o al menos puede ser soslayado mediante una conveniente selección de la representación. Así, basta con escoger una transformación:
de forma que:

con lo cual desaparecen los tres campos de Higgs no físicos 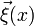 . Debemos aplicar estas transformaciones sobre la suma de las Lagrangianas para bosones y fermiones:
. Debemos aplicar estas transformaciones sobre la suma de las Lagrangianas para bosones y fermiones:
Al final del proceso, tres de los cuatro bosones gauge adquieren masa al absorber cada uno de los tres grados de libertad eliminados del campo de Higgs, gracias a los acoplamientos entre los bosones gauge y el campo Phi presentes en la componente cinética de la Lagrangiana SBS:
Por otro lado, el vacío de la teoría debe ser eléctricamente neutro, razón por la que no existe ningún acoplamiento entre el fotón y el campo de Higgs, h(x), de forma que aquél mantiene una masa nula. Al final, obtenemos tres bosones gauge masivos (W±?, Zµ), un bosón gauge sin masa (A?) y un escalar con masa (h), por lo que seguimos teniendo 12 grados de libertad (del mismo modo que antes: 12 = 3[bosones vectoriales masivos] × 3 + 1[bosón vectorial sin masa] × 2 + 1[escalar]). Los estados físicos de los bosones gauge se expresan entonces en función de los estados originales y del ángulo de mezcla electrodébil ?W:
Ángulo de mezcla
El ángulo de mezcla ?W, se define en función de las constantes de acoplamiento débil, g, y electromagnética, g´, según:
Las predicciones de las masas de los bosones a nivel de árbol son:
donde (e es la carga eléctrica del electrón):
Masa del bosón de Higgs
La masa del bosón de Higgs se expresa en función de ? y del valor de la escala de ruptura de simetría, ?, como:
La medida de la anchura parcial de la desintegración:
a bajas energías en el SM permite calcular la constante de Fermi, GF, con gran precisión. Y puesto que:
se obtiene un valor de ? = 246 GeV. No obstante el valor de ? es desconocido y por tanto la masa del bosón de Higgs en el SM es un parámetro libre de la teoría.
Bosones gauge y fermiones
Análogamente al caso de los bosones gauge, los fermiones adquieren masa mediante los denominados acoplamientos de Yukawa, que se introducen a través de una serie de nuevos términos en la Lagrangiana:
donde:
Del mismo modo que antes, se aplica la transformación sobre la parte levógira de los fermiones, mientras que la parte dextrógira no se transforma:
Y finalmente se obtienen las masas de los fermiones según:
Es conveniente hacer notar en este punto, que la determinación de la masa del bosón de Higgs, no explica directamente las masas fermiónicas ya que dependen de las nuevas constantes ?e, ?u, ?d, … Por otro lado, se deduce también el valor de los acoplamientos del bosón de Higgs con los distintos fermiones y bosones, los cuales son proporcionales a las constantes de acoplamiento gauge y a la masa de cada partícula.
Ya tendremos más sobre el tema
Jul
5
¡Los Campos de Higgs! ¿Que es eso?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (6)
Comments (6)
Los campos de Higgsrompen la simetría de gran unificación y, de no encontrarlo, ¿Sería como un empezar de nuevo?
Bueno, no exactamente. Pero, soy de la opinión que no debemos adelantar los acontecimientos y, debemos tener todas nuestras esperanzas puestas en que, la física teórica está próxima a obtener un gran éxito: confirmando la potencia de la simetría para conformar de manera correcta nuestros razonamientos matemáticos cuando se aventura en las profundidades de lo desconocido de la Naturaleza. Parece que estamos cerca y, si la noticia es confirmada…
Otro triunfo de la aparición del Bosón de Higgs, sería la confirmación de que, las fuerzas, en tiempos pasados eran una sola fuerza, es decir, el universo era parte de un todo simétrico que se desgarró en lo que actualmente conocemos. Por otra parte, sabiendo de la existencia del océano de Higgs, nuestra noción del espacio vacío tendría que ser re-establecida. Un espacio vacío no tiene que ser sinónimo de la NADA ABSOLUTA que, según parece, como la eternidad y lo infinito, no existen.

En Física, cuando hablamos del Campo de Higgs, todos pensamos, de inmediato, que es el campo responsable de la ruptura de simetría asociado con el Bosón de Higgs. El Campo de Higgs puede ser tanto una cantidad escalar elemental como el campo asociado con un estado ligado de dos fermiones. En el Modelo Winberg-Salam, el Campo de Higgs se considera como un campo escalar. En realidad no se saber si estas hipótesis son correctas o no (ahora esperamos que, con “la aparición del Bosón de Higgs, algo más nos digan al respecto), aunque intentos de construir una teoría electrodébil con estados ligados para el Campo de Higgs, conocidos como teorías de Technicolor, no fueron exitosos.
Los Campos de Higgs también aparecen en sistemas de muchos cuerpos que pueden ser formulados como una teoría cuántica de campos con un Bosón de Higgs un ejemplo es la teoría BCS de la superconductividad, en la que el Campo de Higgs está asociado con un par de Cooper, en vez de con un campo escalar elemental.

¿Qué hace? ¿estará buscando el Bosón de Higgs? ¡No hombre! Parece que ya ¡lo encontró!
Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan éstas al campo de Higgs. La influencia de Higgs en las masas de los quarks y de los leptones, nos recuerda el descubrimiento por P. Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.
Hasta ahora no tenemos ni idea de que reglas controlan los incrementos de masa generados por el Higgs (de ahí la expectación creada por el nuevo acelerador de partículas LHC). Pero el problema es irritante: ¿por qué sólo esas masas –Las masas de los W+, W–, y Zº, y el up, el down, el encanto, el extraño, el top y el bottom, así como los leptones – que no forman ningún patrón obvio?

Las masas van de la del electrón 0’0005 GeV, a la del top, mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electro débil (Weinberg-Salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnéticas y débiles. En la unidad hay cuatro partículas mensajeras sin masa los W+, W–, Zº y fotón que llevan la fuerza electro-débil. Además está el campo de Higgs, y, rápidamente, los W y Z chupan la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electrodébil se fragmenta en la débil (débil porque los mensajeros son muy gordos) y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen los teóricos. Prefiero la descripción según la cual el Higgs oculta la simetría con su poder dador de masa.
Las masas de los W y el Z se predijeron con éxito a partir de los parámetros de la teoría electro débil. Y las relajadas sonrisas de los físicos teóricos nos recuerdan que Gerard ´t Hooft y Veltman dejaron sentado que la teoría entera esta libre de infinitos.

Hasta hace algunas decenas de años, se consideraba que el espacio entre las estrellas estaba completamente vacío. Las observaciones ópticas y radioastronómicas han demostrado, en cambio, que éste está lleno de materia interestelar formada predominantemente por hidrógeno mezclado con minúsculas partículas sólidas, llamadas genéricamente polvo interestelar.
Todos los intentos y los esfuerzos por hallar una pista del cuál era el origen de la masa fallaron. Feynman escribió su famosa pregunta: “¿Por qué pesa el muón?”. Ahora, por lo menos, tenemos una respuesta parcial, en absoluto completa. Una vez potente y segura nos dice: “! Higgs ¡” Durante más de 60 años los físicos experimentadores se rompieron la cabeza con el origen de la masa, y ahora el campo Higgs presenta el problema en un contexto nuevo; no se trata sólo del muón. Proporciona, por lo menos, una fuente común para todas las masas. La nueva pregunta feynmariana podría ser: ¿Cómo determina el campo de Higgs la secuencia de masas, aparentemente sin patrón, que da a las partículas de la materia?

Siempre quisimos agarrar la fuente de la que surgía la materia.
Siempre nos hemos preguntado de dónde vino la materia. Hemos llegado a comprender que toda la materia está hecha y es energía concentrada. Con el paso del tiempo pudimos desmenuzar sus componentes y llegamos a ser conscientes de que toda la masa del Universo está conformada a partir de minúsculos objetos que llamamos partículas. Todo lo grande está hecho de cosas pequeñas.
La variación de la masa con el estado de movimiento, el cambio de masa con la configuración del sistema y el que algunas partículas (el fotón seguramente y los neutrinos posiblemente) tengan masa en reposo nula son tres hechos que ponen entre dicho que el concepto de masa sea una tributo fundamental de la materia. Habrá que recordar aquel cálculo de la masa que daba infinito y nunca pudimos resolver; los físicos sólo se deshicieron de él “renormalizándolo”, ese truco matemático que emplean cuando no saben hacerlo bien.
Ese es el problema de trasfondo con el que tenemos que encarar el problema de los quarks, los leptones y los vehículos de las fuerzas, que se diferencian por sus masas. Hace que la historia de Higgs se tenga en pie: la masa no es una propiedad intrínseca de las partículas, sino una propiedad adquirida por la interacción de las partículas y su entorno, y, según mi amigo Ramón Márquez, las partículas toman su masa debido al efecto frenado, cuando en su caminar, se deslizan por los Océanos de Higgs.

La idea de que la masa no es intrínseca como la carga o el espín resulta aún más plausible por la idílica idea de que todos los quarks y fotones tendrían masa cero. En ese caso, obedecerían a una simetría satisfactoria, la quiral, en la que los espines estarían asociados para siempre con su dirección de movimiento. Pero ese idilio queda oculto por el fenómeno de Higgs.
De todas las maneras, va siendo hora ya de que, de una vez por todas, podamos despejar la incognita que desde años atrás ha venido suponiendo el origen de la masa de las partículas y, si como se cree, la fuente está en ese campo de Higgs que ahora trata de sondear el LHC, esperemos que a no tardar mucho, tengamos la respuesta a esa pregunta.
Si al fin aparece el dichoso Bosón de Higgs (y espero que algunas cosas más), sabremos un poco más de los misterios de la Naturaleza y, podremos seguir adelante con la construcción de un Modelo Estándar que, para mi gusto, tiene demasiado parámetros aleatorios para que todo encaje.
¡Veremos qué pasa!

La idea de que la masa no es intrínseca como la carga o el espín resulta aún más plausible por la idílica idea de que todos los quarks y fotones tendrían masa cero. En ese caso, obedecerían a una simetría satisfactoria, la quiral, en la que los espines estarían asociados para siempre con su dirección de movimiento. Pero ese idilio queda oculto por el fenómeno de Higgs.
De todas las maneras, va siendo hora ya de que, de una vez por todas, podamos despejar la incognita que desde años atrás ha venido suponiendo el origen de la masa de las partículas y, si como se cree, la fuente está en ese campo de Higgs que ahora trata de sondear el LHC, esperemos que a no tardar mucho, tengamos la respuesta a esa pregunta.
Si al fin aparece el dichoso Bosón de Higgs (y espero que algunas cosas más), sabremos un poco más de los misterios de la Naturaleza y, podremos seguir adelante con la construcción de un Modelo Estándar que, para mi gusto, tiene demasiado parámetros aleatorios para que todo encaje.
¿El Bosón de higgs! Estará realmente ya, con nosotros.
emilio silvera
















 Totales: 72.382.821
Totales: 72.382.821 Conectados: 23
Conectados: 23




























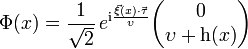


![(\mathcal{D}_\mu \Phi)^{\dagger} (\mathcal{D}^\mu \Phi) = \frac{\upsilon^2}{8}[\mathrm{g}^2 (W_{1\mu}^2 + W_{2\mu}^2) + (\mathrm{g} W_{3\mu} - \mathrm{g}^\prime B_\mu)^2]](http://upload.wikimedia.org/wikipedia/es/math/6/1/6/616cbfafe6476df139c7ad6c4cd80cff.png)