Sep
27
«La cara humana ya está cambiando»
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Evolución ~
Clasificado en Evolución ~
 Comments (0)
Comments (0)
Timothy Bromage, paleoantropólogo
El paleoantropólogo Timothy Bromage describe cómo ha evolucionado nuestro rostro al tiempo que lo ha hecho el cerebro

«La cara humana es única», dice Timothy Bromage, paleoantropólogo de la Universidad de Nueva York. El científico ha participado en un simposio internacional organizado por la Fundación Ramón Areces hace unos días en Madrid para explicar cómo esta parte del cuerpo, capaz de expresar un sin fin de emociones, se ha transformado a medida que lo hacía el cerebro.
-¿Cuándo podemos hablar de la aparición de un rostro que parece humano?

-Si miramos en el registro fósil, encontramos al Homo antecessor (900.00 años), descubierto en la Gran Dolina, en el yacimiento de Atapuerca (Burgos), que tiene aspectos de desarrollo facial que, curiosamente, son muy parecidos a los de los humanos modernos. La forma en la que está organizada la cara en relación con el cerebro se parece más a la nuestra que a la de otros homínidos hallados en la cercana Sima de los Huesos, más similares a los neandertales, como el heidelbergensis.

Heidelbergensis
-¿Y la cara moderna, la nuestra?
-Las raíces de la cara que tenemos ahora comenzaron hace unos 100.000 años, probablemente un poco más. Si miras esa cara no es exactamente como la nuestra actual, pero las raíces se retraen a entonces. La cara humana moderna tiene entre 35.000 y 25.000 años. Su primer dueño fue, con toda seguridad, un africano. Es curioso, porque puedes ver algunos de esos rasgos humanos en homínidos tempranos y no en otros más tardíos, como los neandertales.

Neandertales y sapiens se hibridaron hace más de 100.000 años
-¿Cuál es la característica más distintiva de la cara humana?
-La estructura de nuestra cara ha crecido debajo del cerebro (en vertical) en vez de por delante. De hecho, y en realidad no es sorprendente, la cara humana moderna crece de esta forma (señala su cara de delante hacia atrás). Podemos estudiar esa evidencia en los fósiles.
-Y, aparte del antecessor, ¿es completamente diferente de la del resto de homos?

-Las primeras especies de homo, en sus orígenes, tenían caras muy pronunciadas, mandíbulas salientes, dientes más grandes… Pero luego hubo una reducción de la cara y, al mismo tiempo, un agrandamiento del cerebro, así que esas dos cosas están conectadas.
-¿El desarrollo del cerebro es lo que da forma a la cara?
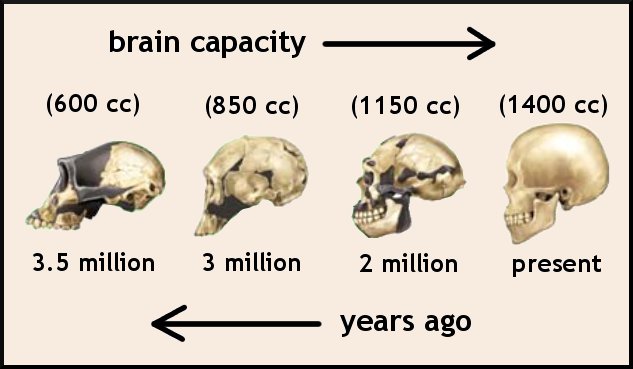
-El tamaño del cerebro está inversamente relacionado con el tamaño de la cara. Cerebro más grande, cara más pequeña. Ambas cosas están unidas y nadie sabe la razón. Algunos creen que es por una cuestión mecánica, para organizar la masa de la cabeza de una forma más eficiente. Si miras a todos los primates, se cumple la misma relación, da igual que no sean homos.
-¿Y ocurre lo mismo con otros animales?
-Nadie lo ha investigado. Hay mucho que averiguar aquí.
-Los neandertales también eran inteligentes, pero tenían una cara muy diferente de la nuestra.

Recreación de grupo de Neandertales en la península Ibérica
-Sí. La diferencia fundamental se encuentra en el medio de la cara. La cavidad para la nariz era más grande y la respiración mucho más expandida. Una explicación para ello es el intento de humidificar y hacer más cálido el aire, para adaptarse a condiciones ambientales frías y secas. Esto incrementaba al capacidad respiratoria de los neandertales. Es una adaptación interesante.
-¿Por qué tenemos la cara que tenemos?

La Evolución es imparable, nada permanece y todo cambia
-La cara incorpora la mayoría de los sentidos del cuerpo, la vista, el sabor, el olor… necesarios para vivir, y eso es importante. Pero también es importante para comer y muchos científicos hablan del sistema masticatorio. Tenemos la cara que tenemos por el tamaño de los dientes, por los músculos que usamos para masticar… todo eso tiene un gran impacto.
-Y sonreímos, guiñamos el ojo, fruncimos la nariz…
-En efecto. Otro factor muy importante es que los humanos tenemos una cara terriblemente expresiva para dar información a otra gente, de forma que puedan leer nuestra mente. Está claro que la cara también tiene un alto significado social, no solo biológico
-¿Somos la única especie que tiene esa habilidad?

Ellos también reflejan en sus caras el estado de ánimo
-No. Incluso Charles Darwin escribió sobre este fenómeno. Es una habilidad que los humanos tenemos particularmente, pero también los simios pueden obtener información de otros miembros del grupo por la expresión facial. Incluso los monos son expresivos, hacen gestos y tienen su comunicación no verbal. Pero el rango de sentimientos que los humanos podemos expresar con nuestra cara es incomparable. Los humanos somos particularmente sensibles a las expresiones de la cara de otras personas.
-¿Y los únicos que nos reconocemos unos a otros por la cara?
-No, no. Estoy seguro de que los grandes simios pueden hacerlo. Hay buenos estudios sobre ello.
-¿Puede la cara humana cambiar en el futuro?

-Lo está haciendo ya. Todos los sistemas evolutivos, como lo es la cara, tienen un propósito y funciones. Si cambias las condiciones de esos propósitos y de esas funciones, entonces la cara cambiará.
-¿Cómo lo está haciendo?
-El mejor ejemplo son los problemas de salud que la gente tiene en la actualidad. Nuestra mandíbula y dientes estaban adaptados a comer comida dura, pero en las sociedades industrializadas hemos dejado de hacerlo. Comemos comida blanda y los huesos no se desarrollan como deben, así que lo que está pasando es que a mucha gente tienen que quitarle los dientes porque no tienen espacio. La función y el propósito cambian por comer un tipo diferente de comida pero no tienes tiempo para evolucionar una nueva cara porque es demasiado rápido.
-¿Hay más consecuencias?
-Otro problema es la apnea del sueño. El espacio para respirar es más pequeño y tienes más riesgo de que no llegue suficiente oxígeno. La apnea del sueño es la consecuencia directa de una reducción innatural de la cara de una persona.
-¿Cómo imagina la cara humana en el futuro?

El aspecto que ofrecerán los humanos dentro de 100 mil años será una frente ancha, ojos grandes y piel pigmentada.
-Ya hay un número cada vez más alto de personas en el mundo que nacen sin el tercer molar (las muelas del juicio), lo que contribuye a una continua reducción en el tamaño de la cara. Es adaptativo, si comes comida blanda, con dos molares basta. Por otro lado, no hay evidencias de que el cerebro esté creciendo. Probablemente haya una reducción en el tamaño de la cara, pero eso será todo lo que veremos en el futuro. Y solo ocurrirá en el mundo industrializado, en el resto, donde todavía comen alimentos duros, no hay estos problemas y sus caras no tienen que cambiar. Todo dependerá de cuánta gente empiece a comportarse como nosotros.
Sep
24
¿La Naturaleza? ¡Simetría dentro de la Diversidad!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo asombroso ~
Clasificado en El Universo asombroso ~
 Comments (0)
Comments (0)

Nuestro mundo, aunque en la Galaxia existan muchos como él (ya han aparecido algunos casi iguales), es un lugar privilegiado que conforma un Ecosistema superior en su conjunto formado por muchos ecosistemas locales aislados los unos de los otros y sin embargo, todos conexionados. La Diversidad de regiones diferentes que existen dentro del mismo planeta es asombrosa y, lo mismo nos podemos encontrar en un lugar como ese que vemos arriba, o en una isla paradisíaca, una selva, un desierto, o perdidos en un inmenso y embravecido océano, en la ventisca de nieve de inmensas montañas y, también, en grutas enormes en las profundidades del planeta.
La NASA descubre el planeta más parecido a la Tierra hallado fuera del Sistema Solar.
Pero todos esos climas diferentes son el resultado de la diversidad y, en cada uno de esos lugares ocurren cosas y, la vida, aunque parezca imposible, está allí presente. Es la consecuencia de que el planeta Tierra esté situado en la zona habitable del Sol, ni demasiado cerca para que la vida perezca achicharrada, ni demasiado lejos para que resulte congelada por el frío. Aquí el agua discurre líquida y cantarina por multitud de lugares y hace posible que, entre el preciado líquido y los rayos del Sol que nos envían la luz y el calor necesarios para la fotosíntesis y la vida… ¡Podamos estar aquí!
Todos sabemos que la materia en nuestro Universo adopta muchas formas distintas: Galaxias de estrellas y mundos que, en alguna ocasión, pueden incluso tener seres vivos y algunos han podido evolucionar hasta adquirir la consciencia. Sin embargo, no me quería referir a eso que es bien sabido por todos, sino que, trato de pararme un poco sobre una curiosa propiedad que la materia tiene en algunas ocasiones y que, la Naturaleza se empeña en repetir una y otra vez: ¡La Simetría!

Las Galaxias espirales, la redondez de los mundos, las estrellas del cielo, los árboles y las montañas, los ríos y los océanos, las especies animales (incluída la nuestra) que, se repiten una y otra vez y, en general, salvando particularidades, todas repiten un patrón de simetría.
Recuerdo aquí aquel pensamiento de Paul Valery en el que nos decía:

“El Universo está construído según un plan cuya profunda simetría está presente de algún modo en la estructura interna de nuestro intelecto.”
Se podría decir que, el Universo está construido según un plan mediante el cual, el logró máximo sería, llegar a los sentimientos.

La Naturaleza está llena de simetrías
La simetría es una propiedad universal tanto en la vida corriente, como desde un punto de vista matemático desde el quehacer de la Física Teórica. En realidad, lo que observamos en la vida corriente es siempre lo repetitivo, lo simétrico, lo que se puede relacionar entre sí por tener algo común. Es siempre lo mismo dentro de una inmensa diversidad formada por grupos iguales.
En un sentido dinámico, la simetría podemos entenderla como lo que se repite, lo reiterativo, lo que tiende a ser igual. Es decir, los objetos que, por mantener la misma geometría, son representativos de otros objetos. En el Caos matemático encontramos concepción de la simetría en el mundo los fractales. Sin embargo, la simetría es mucho más. Hay distintas maneras de expresarla: “Conjunto de invariancias de un sistema”, podría ser una de ellas. Al aplicar una transformación de simetría sobre un sistema, el sistema queda inalterado, la simetría es estudiada matemáticamente usando teoría de grupos. Algunas de las simetrías son directamente físicas. Algunos ejemplos son las reflexiones y las rotaciones en las moléculas y las translaciones en las redes cristalinas.

Aquí hay mucho más de lo que a asimple vista parece
Los físicos teóricos también se guían en sus investigaciones por motivaciones estéticas tanto como racionales. Poincaré escribió: “Para hacer ciencia, es necesario algo más que la pura lógica”. Él identificó ese elemento adicional como la intuición, que supone “el sentido de la belleza matemática”. Heisenberg hablaba de “la simplicidad y belleza de los esquemas matemáticos que la Naturaleza nos presenta”.

La simetría está presente por todas partes y, cada objeto, tiene la suya que siempre, está relacionada con la de otro de la misma especie. Hay simetrías que en física incluye todos los rasgos de un sistema físico que exhibe propiedades de la simetría – eso es, que bajo ciertas transformaciones, aspectos de esos sistemas son “incambiables”, de acuerdo a una observación particular. Una simetría de un sistema físico es un rasgo físico o matemático de un sistema que es preservado sobre cierto cambio.
En matemática, una transformación es un operador aplicado a una función tal que bajo esa transformación, ciertas operaciones sean simplificadas. En ejemplo, en la aritmética cuando se busca un algoritmo de números, el proceso de búsqueda es reducido a la suma de los algoritmos de cada factor.
Por ejemplo, veámos la invariancia de escala: En un recipiente con agua a punto de hervor, las burbujas de vapor, nucleadas en el fondo del recipiente, crecen, se liberan, y fluctúan hasta la superficie de donde se escapan para la atmósfera. A la temperatura de ebullición, el agua existe al mismo tiempo en dos fases distintas – líquido y gas – y a medida que las burbujas se forman las dos fases se separan en el espacio. Si cerramos el recipiente la temperatura de ebullición aumenta, como en una olla a presión. A medida que la presión aumenta, el sistema llega al punto crítico, donde las propiedades del líquido y del gas se vuelven idénticas. Por encima de esa temperatura, en el régimen supercrítico, dejan de existir dos fases distintas y existe apenas un fluido homogéneo.


Cerca del punto crítico, la materia fluctúa sin límites. Burbujas y gotas, unas tan pequeñas como unos cuantos átomos, otras tan grandes como el recipiente, aparecen y desaparecen, se unen y se separan. Exactamente en el punto crítico la escala de las mayores fluctuaciones divergen, pero el efecto de las fluctuaciones en escalas menores no es despreciable. La distribución de las fluctuaciones es invariable para transformaciones de escala.
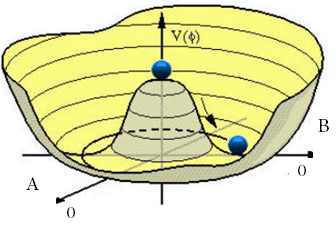
De la figura se deduce que la teoría tiene una “simetría interna”: la figura no cambia cuando hacemos rotaciones en el plano definido por A y B. La invariancia es definida matemáticamente por transformaciones que dejan magnitudes sin cambio. Por ejemplo, la distancia entre dos puntos de un sólido que se mueve, pero no se deforma.
Simetrías locales y globales
Las Galaxias espirales, la redondez de los mundos, las estrellas del cielo, los árboles y las montañas, los ríos y los océanos, las especies animales …
Una simetría global es una simetría que sostiene todos los puntos en el tiempo-espacio bajo consideración, a diferencia de la simetría local que solo sostiene a un subconjunto de puntos.
La mayoría de las teorías físicas son descritas por lagrangianos (En física, un lagrangiano es una función matemática a partir del cual se pueden derivar la evolución temporal, las leyes de conservación y otras propiedades importantes de un sistema físico) que son invariantes bajo ciertas transformaciones, cuando las transformaciones son realizadas en diferentes puntos del espacio-tiempo y están relacionadas linealmente – ellas tienen simetría global.
Por ejemplo, en toda teoría cuántica la fase global de una función de onda es arbitraria y no representa algo físico. Consecuentemente, la teoría es invariante bajo a cambio global de fases (Agregando una constante a la fase de todas las funciones de onda, en todos lados); esto es una simetría global. En la electrodinámica quántica, la teoría es también invariante bajo un cambio local de fase, es decir, que se puede alterar la fase de todas las funciones de onda tal que la alteración sea diferente en cada punto del espacio-tiempo. Esto es una simetría local.

También se habla de ruptura de simetrías temporales en la física de partículas.
Los físicos creen también que están en el camino correcto porque, de algún modo que no pueden explicar, tienen la convicción de que son correctas, y las ideas de simetría son esenciales para esa intuición. Se presiente que es correcto que ningún lugar del Universo es especial comparado con cualquier otro lugar del Universo, así que los físicos tienen la confianza de que la simetría de traslación debería estar las simetrías de las leyes de la Naturaleza. Se presiente que es correcto que ningún movimiento a velocidad constante es especial comparado con cualquier otro. De modo que los físicos tienen confianza en que la relatividad especial, al abrazar plenamente la simetría entre todos los observadores con velocidad constante, es una parte esencial de las leyes de la Naturaleza.

Se dice que esta ecuación de Euler es la más bella conocida. Aunque son muchas las ecuaciones que podríamos traer aquí y que son de todos conocidas y han quedado como símbolos en la historia de las matemáticas, la de Euler, es posible que por su elegancia y simplicidad, le pueda ganar a las demás en belleza. Ahí, en ese sencillo conjunto, los números más significativos de las matemáticas se abrazan: o, 1, e, π, y la unidad imaginaria i .
Si se fijan en la fórmula, en ella aparecen los 5 números más importantes en la historia de las matemáticas. El 0 y el 1 que, entre otras aportaciones a esta disciplina, son famosos por ser elementos neutros y, por lo tanto, indispensables en las operaciones de suma y producto; los números π y e, posiblemente, los dos irracionales más famosos (junto con φ, la razón aúrea) que existen (y que nos permiten hacer el chiste aquel de que la parte más irracional de nuestro cuerpo es el pi-e); y la unidad imaginaria, i, cuyo valor es
Dirac nos hablaba de ecuaciones bellas. La estética es, evidentemente, subjetiva, y la afirmación de que los físicos buscan la belleza en sus teorías tiene sentido sólo si podemos definir la belleza. Afortunadamente, esto se puede , en cierta medida, pues la estética científica está iluminada por el sol central de la simetría.

La Naturaleza nos la muestra por todas partes
La simetría es un concepto venerable y en modo alguno inescrutable y no podemos negar que tiene muchas implicaciones en la Ciencia, en las Artes y sobre todo, ¡en la Naturaleza! que de manera constante nos habla de ella. Miremos donde miremos…¡allí está!

El físico chino-norteamericano Chen Ning Yang ganó el Nóbel de Física por su en el desarrollo de una teoría de campos basada en la simetría y, aún afirmaba: “No comprendemos todavía el alcance del concepto de simetría”. Es lógico pensar que, si la Naturaleza emplea la simetría en sus obras, la razón debe estar implicada con la eficacia de los sistemas simétricos.

En griego, la palabra simetría significa “la misma medida” (syn significa “juntos”, como en sinfonía, una unión de sonidos, y metrón, “medición”); así su etimología nos informa que la simetría supone la repetición de una cantidad medible. Pero la simetría los griegos, también significaba la “la debida proporción”, lo que implicaba que la repetición involucrada debía ser armoniosa y placentera, como de hecho, resultan ser en las imágenes que arriba contemplamos. Asi, la Naturaleza nos está indicando que una relación simétrica debe ser juzgada por un criterio estético superior.

Humo simétrico
Muchos de nosotros, la mayoría, conocimos la simetría en sus manifestaciones geométricas de aquellas primeras clases en la Escuela Elemental, más tarde en el arte y, finalmente, la pudimos percibir en la Naturaleza, en el Universo y en nosotros mismos que, de alguna manera, somos de ese Universo de simetría.
Los planetas son esféricos y, por ejemplo, tienen simetría de rotación. Lo que quiere indicar es que poseen una característica -en caso, su perfil circular- que permanece invariante en la transformación producida cuando la Natuiraleza los hace rotar. Las esferas pueden Hacerse rotar en cualquier eje y en cualquier grado sin que cambie su perfil, lo cual hace que sea más simétrica.

La clave de la belleza está en la simetría, o no.
La simetría por rotación se encuentra en los pétalos de una flor o en los tentáculos de una medusa: aunque sus cuerpos roten, permanecen iguales. La simetría bilateral que hace que los lados derecho e izquierdo sean iguales y se presenta en casi todos los animales, incluido nosotros. Pero es uniendo estos aspectos se obtienen figuras realmente armoniosas. Si se trata de desplazamiento y rotación en un mismo plano hablamos de una espiral, mientras que en el espacio sería una hélice, aunque ambas se encuentran por todas partes en la naturaleza.
Las simetrías se generan mediante las fuerzas que actúan sobre los cuerpos, descritas por leyes rigurosas e inequívocas, como una fórmula matemática y dependen de la existencia de fuerzas distintas que actúan en diversas direcciones. Si éstas permanecen en equilibrio, no hay preferencia alguna hacia arriba o abajo, a la derecha o a la izquierda, y los cuerpos tenderán a ser perfectamente esféricos, como suele ocurrir en el caso de virus y bacterias, las estrellas y los mundos… las galaxias. Además, cuando el aspecto no es el de una esfera perfecta, la Naturaleza hará todo lo posible para hacercarse a esta.

La simetría también están prtesentes en nuestros cerebros
¿Sería posible que la simetría material tuviera un paralelismo en la abstracción intelectual que son las leyes físicas? luego hace falta un esfuerzo mental considerable para pasar de lo material a lo intelectual, pero cuando se profundiza en ellla, la conexión aparece. En la naturaleza existen muchas cosas que nos pueden llevar a pensar en lo complejo que puede llegar a resultar entender cosas que, a primera vista, parecían sencillas.
Me explico:

Fijémonos, por ejemplo, en una Flor de Girasol y en las matemáticas que sus semillas conllevan. Forman una serie de números en la que cifra es la suma de las dos precedentes (por ejemplo 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…) se denomina, en términos matemáticos, sucesión de Fibonacci, una ley que se cumple incluso en el mundo vegetal, como hemos podido comprobar en las semillas del girasol, dispuestas en espiral y que respetan ésta fórmula. La podemos ver por todas partes.

Lo mismo ocurre con otros ejemplares de la diversidad del mundo de las plantas
En el mundo inorgánico las leyes de la cristalización del agua congelada, determinadas por las fuerzas que actúan entre las moléculas, hacen que los cristales adopten formas que son infinitas y varían con respecto a un tema común: la estrella de seis puntas. Sin embargo, los planetas son esféricos porque han nacido en la primordial que rodeaba al Sol, atrayendo materia indiferentemente de todas partes.

Claro que, en la Naturaleza, nada ocurre porque sí, todo tiene su por qué, y, todo lo que en ella podemos contemplar posee una funcionalidad que está directamente relacionada con su mecánica, con el medio en el que habita, con lo que el Universo espera que haga en su medio y, para ello, dota a figura con aquellos “trajes” que mejor les permita realizar aquello para lo que están destinados.
Vamos a generalizar un paso más el concepto de simetría, planteándonos si es posible que una ley física se cumpla en cualquier lugar. ¿En cualquier lugar… de dónde?, ¿de nuestra ciudad?, ¿de nuestro planeta? No: del universo. Una ley que fuera válida en cualquier lugar del universo sería una ley simétrica respecto al espacio. Se cumpliría dondequiera que se hiciese un experimento para comprobarla.


La masa es energía congelada, en presencia de grans masas el espacio se curva, la velocidad de la luz marca el límite de enviar información en nuestro Universo…
Fíjense que nuestra idea de simetría se va haciendo más compleja y más profunda. no nos detenemos en ver si la forma material de un objeto es simétrica, ni de si la escritura de una fórmula matemática es simétrica. Ahora nos preguntamos si una ley física es válida en todo el Universo.
La otra simetría interesante para una ley física es la que se refiere al tiempo. Cierta ley física se cumple ; ¿antes también?, ¿se cumplirá pasado algún tiempo? Una ley que fuera cierta en cualquier instante de la historia del universo sería una ley simétrica respecto al tiempo.

Lo que nos preguntamos es: ¿son simétricas o no las leyes de la física?
Hasta donde alcanzan nuestras medidas, las leyes físicas (y, por tanto, la interacción gravitatoria) sí son simétricas respecto al espacio y respecto al tiempo. En cualquier lugar y momento temporal del universo, la Naturaleza se comporta igual que aquí y ahora en lo que se refiere a estas leyes.
Esta simetría es un arma muy poderosa para investigar hacia el pasado y hacia el futuro, ya que nos permite suponer (y, en la medida en que confiemos en la seguridad de la simetría,conocer) locales donde jamás podremos llegar por la distancia espacial y temporal que nos separa de muchas partes del universo. Así, por ejemplo, gracias a esta simetría, podemos calcular que el Sol lleva 5.000 millones de años produciendo energía y que le quedan, probablemente, otros 5.000 millones hasta que consuma toda su masa. Esto lo podemos aventurar suponiendo que en ese enorme tramo de 5.000 + 5.000 = 10.000 millones de años las leyes físicas que determinan los procesos mediante los cuales el Sol consume su propia masa como combustible (las reacciones nucleares que le permiten producir energía), fueron, son y serán las mismas aquí en el Brazo de orión donde nos encontramos como en los arrabales de la Galaxia Andrómeda donde luce una estrella como nuestro Sol que, también envía luz y calor a sus planetas circundantes, y, por muy lejos que podamos mirar, siempre veremos lo mismo.

Por tanto, en cierto modo, la simetría se vuelve tan importante o más que la propia ley física.
La regularidad de las formas de la Naturaleza se refleja incluso en la cultura humana, que desde siempre intenta inspirarse en el mundo natural conformar su propio mundo. Existen hélices en las escaleras de palacios, castillos y minaretes y en las decoraciones de esculturas y columnas. Las espirales abundan en los vasos, en los bajorrelieves, en los cuadros, en las esculturas en los collares egipcios, griegos, celtas, precoolombinos e hindúes e, incluso, en los tatuajes con los que los maoríes neozelandeses se decoran el rostro.

¿Tenía en mente Leonardo la proporción áurea a la hora de realizar su obra maestra? Afirmarlo resultaría aventurado. Menos polémico es aseverar que el genio florentino concedía gran importancia a la relación entre la estética y la matemática. Dejaremos la cuestión en el aire por el momento, no sin antes mencionar que Leonardo realizó las ilustraciones de una obra de contenido estrictamente matemático, escrita por su buen amigo Luca Pacioli, llamada “De divina proportione”, es decir, “La divina proporción”.
Fuente de esta imagren y texto: Fernando Corbalán
La búsqueda de la perfección geométrica y de las propiedades matemáticas pueden ser una guía importante en el estudio científico del mundo. Paul Dirac, una de los padres de la moderna mecánica cuántica, solía decir que “si una teoría es bella desde el punto de vista matemático, muy probablemente es también verdadera”.

A todo esto, no debemos olvidar que todo, sin excepción, en nuestro Universo, está sometido a la Entropía que nos trae el paso inexorable de eso que llamamos “Tiempo”, y que, convierte perfectas simetrias de joven belleza, en deteriorados objetos o entidades que, nos viene a recordar que nada es perpetuo, que todo pasa y se transforma. Claro que, de alguna manera, todo vuelve a resurgir.
María Silvera presentará un concierto del Renacimiento al barroco: el virginal, el próximo viernes en la Iglesia de San Clemente (Segovia) a las 20:00 del 19 de Diciembre. Su programa es un viaje por países donde este instrumento tuvo un desarrollo importante: Inglaterra, Italia y España.
Un dolor que llevo dentro de mí es el no poder contemplar la verdadera belleza que estándo presente en los seres vivos inteligentes, en la mayoría de los casos, se nos queda oculta a nuestra percepción, toda vez que esa clase de belleza, que no podemos ver pero sí percibir, sólo la podemos captar con el trato y la convivencia y, verdaderamente, tengo que admitir que, algunas bellezas que he tenido la suerte de poder “ver con los ojos del espíritu”, llegan a ser segadoras, deslumbrantes, su explendor es muy superior al de la estrella más brillante del cielo, y, seguramente (estoy seguro) como a muchos de ustedes les pasa, tengo la suerte de tenerla junto a mí desde hace muchos años. y, si pienso en ello en profundidad y detenimiento, no tengo más tremedio que concluir que es ese brillo y esplendor el que me da la fuerza para seguir cada dia en la dura lucha que nos ha participar.
¡Sí que es importante la Belleza! Dirac tenía toda la razón. Y, no digamos las Simetrías que indican con el dedo de la Naturaleza el camino a seguir a muchos físicos que quieren desvelar sus secretos.
emilio silvera
Sep
23
El Espacio, ese sueño nuestro de ir a las estrellas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Futuro ~
Clasificado en Futuro ~
 Comments (0)
Comments (0)
MOTOR WARP El Universo Viaje Espacial – YouTube

Aquí os dejo un video de You Tube que nos habla del sueño de viajar a las estrellas y también, de sus muchos invonvenientess. No sabemos como dominar la fuerza de Gravedad, no sabemos como paliar los inconvenientes para viajar en el vacío espacial, no sabemos…. ¡tántas cosas! oigamos lo que nos dicen.
Es una lástima que, científicos reputados, no tengan la habidad de saber contarnos las cosas con más sencillez, de manera tal que, llegue a nosotros el mensaje de manera sencilla para que lo podamos comprender.
Pero tal cosa, no parece fácil ni está en posesión de cuaqlquiera, así que, oigamos lo que tenemos.
Sep
22
SABER QUE SE PUEDE, CREER QUE SE PUEDA”
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Cerebro y Mente ~
Clasificado en Cerebro y Mente ~
 Comments (10)
Comments (10)

Hoy día podemos considerar que existen dos posturas enfrentadas acerca del funcionamiento del Universo. Por un lado están los que piensan que el Universo es cómo es debido al azar y, en el bando opuesto, están los que consideran que existe un patrón oculto, una especie de imperativo cósmico que subyace encriptado en las leyes que rigen la naturaleza, la materia, los ciclos de los planetas o la vida en general.
Ambas posturas presentan sólidos argumentos a su favor, argumentos que aunque puedan ser criticados no por ello están exentos de razón. Los que dan crédito a la posibilidad del azar básicamente sustentan su opinión en el comportamiento que observamos en las partículas a nivel fundamental. En este nivel, que es el nivel al que se encuentran las partículas más pequeñas que podemos detectar, ciertamente todo parece regirse en base a la probabilidad. Los que opinan, por el contrario, que existe una especie de “orden implicado” básicamente basan sus creencias en la irrazonable efectividad que presentan las matemáticas para describir la realidad.

La analogía del relojero es un argumento teleológico que sostiene que el diseño implica un diseñador. Ha tenido un papel prominente en la teología natural y el “argumento del diseño”, donde se ha usado para argüir a favor de la existencia de Dios y el diseño inteligente del universo.(la imagen y el pequeño texto de abajo no pertenecen al trabajo original, y, sólo se añade para hacer más dinámica la lectura).
Ciertamente parece complicado conciliar ambas posturas. Si es cierto que existe una especie de “diseño inteligente” ¿Cómo podría éste basarse en el azar o la probabilidad? Pero si, por el contrario, todo se debiera al azar ¿Cómo explicamos que nuestras leyes universales se basen en criterios que involucran una lógica racional?
La única posibilidad de unificar ambos criterios sería aceptar que existe una manera de organizar el azar de forma racional, una especie de “principio cosmo-caótico” al que hizo referencia Celeb Scharf. Si esto fuera cierto simplemente implicaría que la lógica que subyace en el comportamiento de todo cuanto acontece en el Universo sería la más simple que cabría imaginar, dado que exigiría únicamente la combinación de dos elementos: uno y su opuesto, que es la única condición que permite o acepta el criterio del azar. En otras palabras, si pudiéramos unificar ambas posturas en una teoría global o unificada implicaría que lo imposible es la única posibilidad. Pues bien, de esta posibilidad es de la que vamos a hablar, de qué manera se puede “materializar” el azar.

Esta proporción ha fascinado desde hace siglos al ser humano, que lo ha considerado un indicador de la perfección y la estética.
Para ello utilizaré un patrón “oculto” que hace ya tiempo descubrimos en la naturaleza, tratando de seguir su rastro para ver dónde nos lleva. Se trata de la “Proporción Áurea”, a veces denominada “Divina Proporción”.
La proporción áurea es perfecta cómo ejemplo para explicar todos estos aspectos tan contradictorios de la naturaleza y de paso entender la esencia de una teoría unificada. Esta relación puede describirse tanto de forma física como de forma matemática, es compatible con el criterio del azar y además representa un patrón organizado de comportamiento en sí misma. Es un patrón que además es independiente de la forma que tengamos de referirnos a él: es una proporción intemporal que ha existido siempre y siempre existirá. Si una civilización situada en el extremo opuesto del Universo la descubriera seguramente utilizaría una simbología completamente distinta de la nuestra, pero lo que nunca podría hacer es alterar su esencia. Se trata, por tanto, de un patrón tan universal cómo podría serlo la relación entre el diámetro y el arco de una circunferencia.

De acuerdo con el conocido físico y divulgador Paul Davies (la existencia de patrones intemporales de comportamiento) “(…) implica que las leyes del Universo han diseñado su propia comprensión y que la mente y el conocimiento no son más que subproductos derivados de su evolución”. Si esto fuera cierto implicaría necesariamente que las leyes universales que conocemos no sólo gobiernan nuestra existencia, sino que también gobiernan nuestros pensamientos (Se trata del conocido “Pienso, luego existo”). Este autor acaba su frase diciendo: “Esta es una asombrosa visión de la naturaleza, magnífica y estimulante en su majestuosa visión de conjunto. Espero que sea correcta. Sería maravilloso si fuera correcta. Pero si lo es, representaría un cambio en la cosmovisión científica tan profundo como el iniciado por Copérnico y Darwin juntos”.
Suele utilizarse el ejemplo de la reproducción de los conejos para explicar la proporción áurea, dado que fue el ejemplo que utilizó su descubridor, Fibonacci, para exponerla. Aunque serviría igual si utilizamos patos, seres humanos o partículas. Este pensador equiparó las virtudes matemáticas de la divina proporción con “Dios”, entre otros motivos porque en cualquier unidad de medida dada siempre habrá una proporción áurea implicada

Comencemos. Tomemos una pareja macho-hembra de conejos. Estos se encuentran, se gustan y sin más preámbulos llevan a cabo la fecundación. Al mes exacto del feliz encuentro dan a luz a una nueva pareja de conejos macho-hembra. Al final del primer mes, por tanto, tenemos dos parejas: una pareja adulta y una pareja de conejos bebe. Los conejos bebe han de esperar un mes para alcanzar la fertilidad y poder fecundar. La pareja adulta no se espera y el mismo día del feliz alumbramiento, haciendo honor a su fama, la hembra vuelve a quedarse preñada. Al final del segundo mes, por consiguiente, tenemos tres parejas: la pareja inicial, la pareja de bebes convertidos en adultos fértiles y la nueva pareja que acaba de nacer.
Si seguimos esta progresión al final del tercer mes tendremos 5 parejas, dos parejas adultas, una pareja que acaba de alcanzar la edad fértil, y dos parejas de bebes conejo que acaban de nacer. Al final del cuarto mes tendremos 8 parejas y así sucesivamente….
La relación que existe entre el número de parejas de un mes dado en comparación con el número de parejas del mes precedente es la que va componiendo progresivamente el valor que conocemos como proporción áurea o sucesión de Fibonacci (2/1, 3/2, 5/3, 8/5, 13/8, 21/13, etc….) Cada vez que una pareja alcanza la edad adulta una nueva secuencia comienza y se “entrelaza” con la anterior generación en el tiempo.

Bueno… pues ¡Manos a la obra!….
Vamos a empezar a “descomponerla”…
Comencemos eliminando los conejos de la sucesión. Aunque sean prácticos en el ejemplo no son necesarios; Cualquier pareja de elementos con la capacidad de auto-duplicarse a sí misma nos serviría.
Sigamos eliminando conceptos innecesarios. Eliminemos el factor-tiempo. En el ejemplo hemos utilizado la magnitud “mes” como periodo de fertilidad o duplicación. Pero la sucesión no cambiaría su aspecto si en lugar de un mes fuera un día, un simple segundo o incluso si la duplicación fuera casi instantánea.
Ahora podemos observar más claramente la simplicidad de su comportamiento: “Pasado un cierto tiempo (sea el que sea) tiene lugar la aparición de un nuevo elemento” ¡Ya está!, No hay más… ese es todo su “secreto”.

Parece sencillo ¿No es cierto? Pues bien, en la comprensión o el descubrimiento de este sencillo funcionamiento se asienta lo que conocemos como “mecánica cuántica”, basada en que cada cierto tiempo un electrón emite (de forma “espontánea”) un fotón. En terminología algo más técnica diríamos que las oscilaciones electromagnéticas se suceden de forma cuantificada (unitaria) y la energía implicada está directamente relacionada con la frecuencia.
¿Cada cuánto tiempo sucede esto? Lo cierto es que es difícil responder a esta pregunta porque no tenemos manera de cuantificar este suceso. Sabemos que ocurre de forma “casi” instantánea (si lo observamos a escala humana) pero no hay forma ni manera de establecer un criterio objetivo basado en el tiempo.
La única manera paralela que tenemos de hacerlo no es utilizando un criterio basado en el tiempo, sino utilizando un criterio basado en la frecuencia o la probabilidad. Si tenemos 137 electrones uno de ellos emitirá espontáneamente un fotón; Dicho de otra manera, la probabilidad de que se emita un fotón en un instante dado de tiempo es 1/137. A este cociente lo llamamos “Constante de estructura fina” y se trata de la constante más representativa de toda la física conocida. Aunque no lo parezca a primera vista este cociente es el resultado de mezclar tres constantes fundamentales de la naturaleza: la velocidad de la luz, la constante de Planck y la carga del electrón. Lo más sorprendente de esta constante es que no viene definida por ninguna unidad física de medida, es un simple número… ¡Sin más!
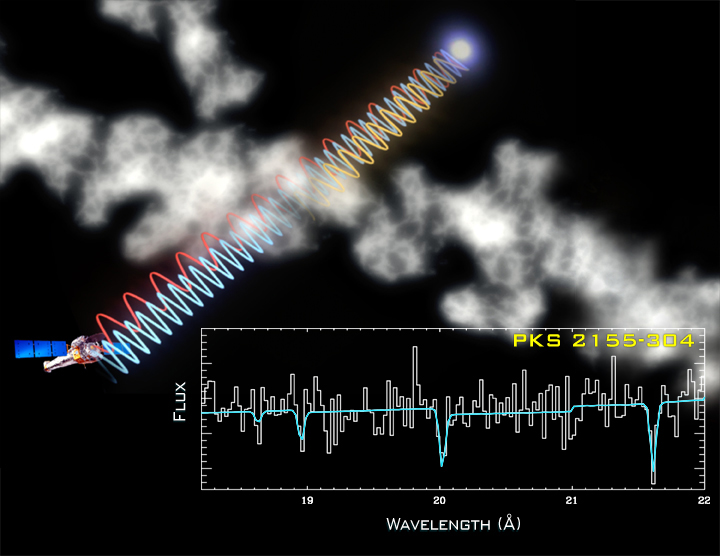
Sí, parece que todo es una aventura en el Universo
A veces se denomina “Constante de acoplamiento universal” y nos proporciona una referencia de lo milimétricamente diseñado que está el Universo, pues si su valor cambiara ligeramente no existiría el Universo cómo lo conocemos. Dada su independencia respecto del tiempo, su esencia continua inalterada: cada cierto tiempo algo pasa dentro del electrón y el resultado es que se emite (o absorbe) un fotón. Esta constante (como vemos) conserva la misma esencia en que se basa la divina proporción.
A esta actividad (no sabemos si frenética o no) que tiene lugar en los núcleos atómicos a veces se le denomina “Energía del vacío” (la energía que surge de la nada, la “Chispa de la Creación”) y básicamente implica que toda partícula en el Universo tiene literalmente una especie de” vida interior”, una vida que se expande en base a este movimiento de duplicación y que es el germen primigenio de lo que denominamos “Expansión del Universo”. Como sabemos gracias a Edwin Hubble el Universo se está expandiendo, lo que implica que las galaxias se alejan unas con respecto de las otras desde el principio de los tiempos. A veces decimos que la expansión del Universo no tiene sentido físico, dado que no sabemos lo que implica que tanto el espacio como el tiempo se estén creando en este mismo momento.
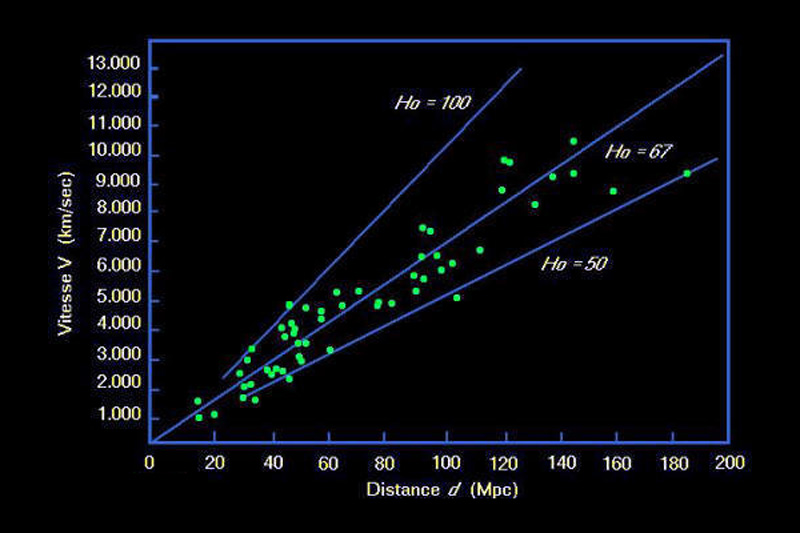
La imagen original era más atractiva pero, la página no la aceptó
Pero lo más sorprendente no es que este movimiento duplicativo o expansivo no tenga sentido físico, lo más sorprendente es que tan sólo podamos definirlo en base a relaciones numéricas. Pero incluso en este sentido este comportamiento guarda una extraña y misteriosa correlación con la “divina proporción” pues este patrón se basa también única y exclusivamente en relaciones numéricas.
Heisenberg, quien formuló la ley fundamental de la mecánica cuántica (que básicamente establece que un estado cuántico es indeterminado) solía decir que los átomos no son cosas, sino que son “tendencias” ¿Podemos aplicar también esta idea a nuestra mágica proporción? Pues resulta que sí, que también podemos hacerlo.
Aunque parezca paradójico la divina proporción es un teorema matemático (en el sentido de que sigue una regla de comportamiento) y no lo es al mismo tiempo. Un teorema podemos definirlo como una regla estática de equilibrio; Sin embargo dicha proporción es una regla dinámica, un valor que se va aproximando a él mismo a medida que vamos añadiendo más y más decimales a su valor. La divina proporción representa una tendencia, siendo ésta además una tendencia indeterminada, dado que se trata de una sucesión que nunca se acaba. De forma matemática la proporción áurea es una imposibilidad pero, sin embargo… ¡Ahí está!
Max Planck
Max Planck decía que: “La materia se origina y existe sólo en virtud de una fuerza que hace vibrar las partículas del átomo” refiriéndose a éste como el más diminuto de los sistemas solares. Poco tiempo después de sus descubrimientos los físicos comprendieron que las matemáticas que describen las frecuencias del sonido emitido por un tambor podían usarse también para calcular los niveles energéticos de vibración de los electrones en un átomo. El problema era descifrar la forma del tambor matemático que determinaba esos niveles energéticos del núcleo. La sorpresa fue descubrir que una función matemática creada por Riemann para tratar de cartografiar la distribución de los números primos coincidía a la perfección con las distribuciones que ellos buscaban. Resultaba que los “átomos de los números” y los “átomos de la materia” se encontraban sometidos a la misma distribución o a la misma estructura.
Cuando decimos que un patrón (matemático o no) es intemporal o independiente del tiempo también solemos referirnos a este hecho diciendo que la información que transmite tan sólo existe en un tiempo imaginario, una especie de plano temporal que opera en una dimensión no-material. El mejor ejemplo para describir esto lo encontramos en el teorema más famoso de la humanidad: el “Teorema de Pitágoras”. Dicho teorema, al margen de las aplicaciones prácticas que todos conocemos, establece una especie de verdad inmutable y universal: “Siempre que tengamos dos elementos absolutamente opuestos entre ellos, dichos elementos estarán relacionados”.
En el caso de la divina proporción esto no sólo es cierto, sino que dicha relación por si sola ya define la misma relación en que se basa el Teorema de Pitágoras. Y es que la divina proporción es el único valor matemático cuyo valor y su valor opuesto resultan ser el mismo valor; Algo aparentemente imposible, pero cierto.
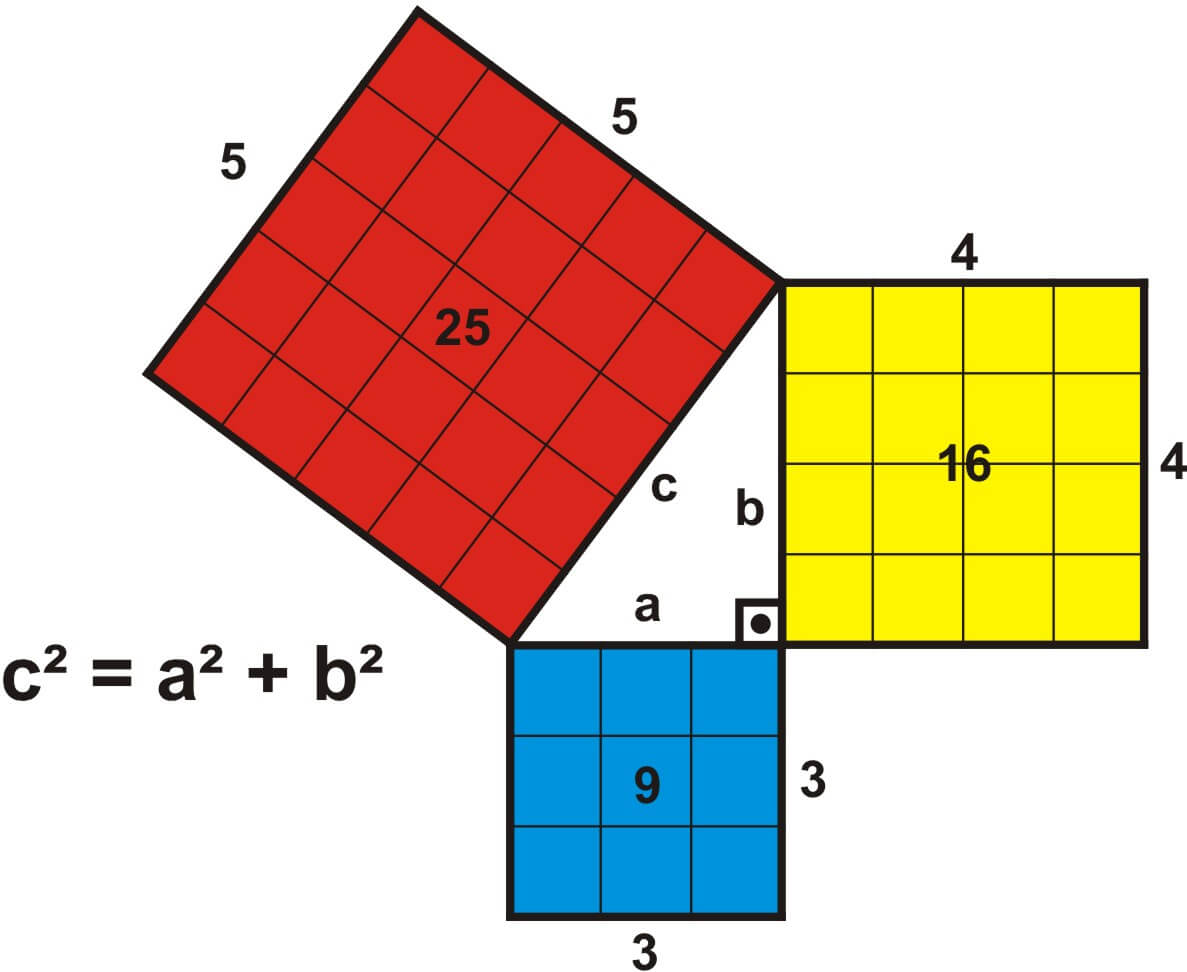
El Teorema de Pitágoras es muy especial. No sólo por ser el único criterio capaz de unificar toda la geometría conocida, sino porque constituye la única regla de Entrelazamiento Dimensional entre dos elementos conocida en matemáticas. Es lo que se conoce como “Conjetura de Fermat” que (básicamente) establece que en el Universo matemático tan sólo es posible relacionar dos elementos opuestos entre ellos cuando los elevamos al cuadrado. Esta propiedad tan sorprendente es la base de lo que conocemos como “Ley de la Gravedad”, que dictamina que dos elementos tan opuestos entre ellos como son las masas y las distancias que las separan coinciden en una dimensión diferente: la dimensión de los cuadrados de sus elementos.
De hecho, la relación de los cuadrados está presente en todos lados donde hemos podido encontrar un patrón de comportamiento. La ondulatoriedad en mecánica cuántica se basa en el cuadrado absoluto de la función de onda, la fuerza electromagnética se debilita en proporción inversa al cuadrado de la distancia entre dos fuerzas eléctricas; Incluso los planetas dan vueltas alrededor del Sol en tiempos cuyos cuadrados son iguales a los cubos de sus distancias.

Pero… ¿Qué sentido físico tiene la elevación al cuadrado? Lo cierto es que tampoco lo sabemos porque queda literalmente en una dimensión diferente. Nuestra capacidad de captar el mundo a través de los sentidos es lineal, de la misma forma que lo es nuestra forma de pensar. No podemos pensar en dos cosas al mismo tiempo y por este motivo la única operación lógica que puede hacer nuestro cerebro es “triangular”.
Las coincidencias son sorprendentes. La proporción áurea es el único valor que incorpora automáticamente una dimensión matemáticamente posible, pero físicamente inexistente. Se trata de un valor doblemente irracional, no tan sólo por incorporar el infinito en su formulación, sino por incorporar también el plano imaginario, que es precisamente el plano que da sentido a la descripción probabilística del mundo a nivel cuántico o fundamental.
Como indican los controvertidos físicos y gemelos Bodganov: “Los grandes teóricos de los números están convencidos: en el corazón de estas series interminables, en esos miles de millones de cifras que giran en el infinito hay un secreto. Una clave que, abriendo las puertas del infinito, nos hace regresar al cero. Y por tanto a la creación del Universo”.
No podría estar más de acuerdo. Es más, creo que es cierto y que existe una demostración maravillosa al respecto. A fin de cuentas, si es cierto que el Universo se basa en la probabilidad, tan sólo es cuestión de tiempo que lo imposible se haga realidad.
Ricard Jiménez
Sep
21
¡Nuestra curiosidad! Siempre desvelando misterios
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Divagando ~
Clasificado en Divagando ~
 Comments (1)
Comments (1)

En cierta ocasión, Leonardo Da Vinci contaba:
“Arrastrado por mi apasionado deseo, anhelante de ver la gran confusión de las variadas y extrañas formas creadas por la ingeniosa Naturaleza, vagué durante un tiempo entre
los oscuros acantilados y llegué a la entrada de una gran caverna. Permanecí delante de ella por un tiempo, estupefacto, e ignorante de la existencia de algo semejante, con la espalda curvada y la mano izquierda apoyada en las rodillas, y protegiéndome los ojos con la derecha, con los párpados bajos y semicerrados, inclinándome a menudo de un lado y otro para ver si podía distinguer algo del interior; pero no pude por la gran oscuridad que allí había. Y después de permanecer así un rato, de pronto surgieron en mí dos sentimientos, temor y deseo; temor de la amenazante caverna oscura, y deseo de ver si había dentro algo milagroso.”
La historia es un fiel reflejo metafórico de lo que sentimos cuando, ante nosotros, se nos presenta algo que no llegamos a comprender y que nos da miedo abordar pero , prevalece el deseo y la curiosidad que sentimos por desvelar aquel misterio y llegar a conocer que, se esconce dentro de él. Ese impulso, es el que ha llevado a muchos físicos a realizar descubrimientos que han hecho posible el avance del conocimiento del “mundo”.
, prevalece el deseo y la curiosidad que sentimos por desvelar aquel misterio y llegar a conocer que, se esconce dentro de él. Ese impulso, es el que ha llevado a muchos físicos a realizar descubrimientos que han hecho posible el avance del conocimiento del “mundo”.

Estar cerca de un agujero negro y sentir las fuerzas que te atraen y espaguetiza tu cuerpo para engullirlo…
Aquí vemos la entrada a otra “Gruta de Leonardo” en la que no sabemos que fuerzas y energías podrían estar presentes y que fuerzas de marea nos arrastrarían hacia quíen sabe que lugares ignotos situados en otros universos o, por el contrario, en lugar de ser la entrada hacia un mundo maravilloso, sólo se trata del camino que nos lleva hacia la destrucción.
quíen sabe que lugares ignotos situados en otros universos o, por el contrario, en lugar de ser la entrada hacia un mundo maravilloso, sólo se trata del camino que nos lleva hacia la destrucción.
“Lo cierto es que cuanto más aprendamos acerca del mundo y cuanto más profundo sea nuestro aprendizaje, tanto más conscientes, específico y articulado será nuestro conocimiento de lo que no conocemos, nuestro conocimiento de nuestra ignorancia. Pues, en verdad, la fuente principal de nuestra ignorancia es el hecho de que nuestro conocimiento sólo puede ser finito, mientras que nuiestra ignorancia es necesariamente infinita.” Así lo escribió el gran filósofo de la ciencia, Karl Popper.
ser finito, mientras que nuiestra ignorancia es necesariamente infinita.” Así lo escribió el gran filósofo de la ciencia, Karl Popper.
Hay una difundida y errónea suposición de que la ciencia se ocupa de explicarlo todo, y que, por ende, los fenómenos inexplicados preocupan a los científicos al amenazar la hegemonía de la visión del mundo. El técnico en bata del Laboratorio, en la película de bajo presupuesto, se queda mirando para el techo, pensativo y, de pronto, se da una palmadita en la frente cuando se encuentra con algo nuevo , y exclama con voz temblorosa, entrecortada: “¡Pero, no hay explicación para esto!”. En realidad, por supuesto, cada científico digno se apresura a abordar lo inexplicado, pues es lo que hace avanzar la ciencia. Son, a veces, los grandes sistemas místicos de pensamientos, envueltos en terminologías demasiado vagas para ser erróneas, los que explican todo, raramente se equivocan y no crecen.
, y exclama con voz temblorosa, entrecortada: “¡Pero, no hay explicación para esto!”. En realidad, por supuesto, cada científico digno se apresura a abordar lo inexplicado, pues es lo que hace avanzar la ciencia. Son, a veces, los grandes sistemas místicos de pensamientos, envueltos en terminologías demasiado vagas para ser erróneas, los que explican todo, raramente se equivocan y no crecen.

La ciencia es intrínsicamente abierta y exploratoria, y comete errores todos los días. En verdad, ese será siempre su destino, de acuerdo con la lógica esencial del segundo teorema de incompletitud de Kurt Gödel. El teorena de Gödel demuestra que la plena validez de cualquier sistema inclusive un sistema científico, no puede demostrarse dentro del sistema. En otras palabras, la comprensibilidad de una teoría no puede establecerse a menos que haya algo fuera de su marco con lo cual someterla a prueba, algo más allá del límite definido por una ecuación termodinámica, o por la anulación de la función de onda cuántica o por cualquier otra teoría o ley. Y si hay tal marca de referencia más amplio, entonces la teoría, por definición, no lo explica todo.En resumen, no hay ni habrá nunca una descripción científica completa y copmprensiva del universo cuya validez pueda demostrarse. Estamos inmersos en una Naturaleza en la que, estará siempre presente ¡la incertidumbre!. Miramos hacia las lejanas estrellas y nos preguntamos sobre la esencia del universo y, algunas veces, incluso hemos pensados que podríamos ser nosotros.
que haya algo fuera de su marco con lo cual someterla a prueba, algo más allá del límite definido por una ecuación termodinámica, o por la anulación de la función de onda cuántica o por cualquier otra teoría o ley. Y si hay tal marca de referencia más amplio, entonces la teoría, por definición, no lo explica todo.En resumen, no hay ni habrá nunca una descripción científica completa y copmprensiva del universo cuya validez pueda demostrarse. Estamos inmersos en una Naturaleza en la que, estará siempre presente ¡la incertidumbre!. Miramos hacia las lejanas estrellas y nos preguntamos sobre la esencia del universo y, algunas veces, incluso hemos pensados que podríamos ser nosotros.

Sí, tratar de saber es bueno. Sin embargo, nunca llegaremos a saberlo todo
Tal planteamiento, al menos como lo veo yo, es bueno y saludable. Pensemos en el infierno que sería un universo pequeñito al que pudiéramos explorar y comprender totalmente. Alejandro Magno, se dice , lloró cuando le dijeron que había infinitos mundos (“¡Y nosotros no hemos conquistado ni siquiera uno!”, exclamó sollozando), pero la situación parece más optimista a quienes se inclinan a desatar, no a cortar, el nudo gordiano de la Naturaleza.
le dijeron que había infinitos mundos (“¡Y nosotros no hemos conquistado ni siquiera uno!”, exclamó sollozando), pero la situación parece más optimista a quienes se inclinan a desatar, no a cortar, el nudo gordiano de la Naturaleza.
Ningún hombre, o mujer, realmente reflexivo deberían desear saberlo todo, pues cuando el conocimiento y su análisis son completos, el pensamiento se detiene y (cosa que no nos conviene), comienza a desaparecer la curiosidad y el interés por las cosas que, al conocerlas, no encierran ningún misterio que desvelar, con lo cual, la degradación comienza su camino en el interior de nuestras mentes.

La falta de interés nos hace caer en la melancolía, el aburrimiento, nada llama ya nuestra atención
caer en la melancolía, el aburrimiento, nada llama ya nuestra atención

La paradoja del más conocido cuadro de la serie La trahison des images (1928–1929) de René Magritte. Serie sobre la que Foucault escribió un no menos conocido ensayo.
conocido ensayo.
René Magritte, en 1926, pintó un cuadro de una pipa y escribió debajo de él con una cuidadosa letra de escolar (lo que arriba podeis leer) y que, traducido, decía “Esto no es una pipa”. Esta pintura podría convertirse apropiadamente en el emblema de la Cosmología científica. La palabra “Universo” no es el Universo; ni lo son las ecuaciones de la teoría de la supersimetría, ni la ley de Hubble ni la métrica de Friedmann-Walker-Robinson. Generalmente, la ciencia tampoco sirve de mucho para
pintura podría convertirse apropiadamente en el emblema de la Cosmología científica. La palabra “Universo” no es el Universo; ni lo son las ecuaciones de la teoría de la supersimetría, ni la ley de Hubble ni la métrica de Friedmann-Walker-Robinson. Generalmente, la ciencia tampoco sirve de mucho para explicar lo que algo es, y mucho menos, lo que el universo entero, realmente “es”.
explicar lo que algo es, y mucho menos, lo que el universo entero, realmente “es”.
La Ciencia describe y predice sucesos, pero paga por este poder al tener que, rectificar muchas veces, dado que las predicciones que se hacen, son aproximaciones de la realidad que buscamos y que, poco a poco, tratamos de perfeccionar depurando los defenctos de aquellas más viejas con estas otras más nuevas que llevan incorporados nuevos parámetros despuñés descubiertos.
poder al tener que, rectificar muchas veces, dado que las predicciones que se hacen, son aproximaciones de la realidad que buscamos y que, poco a poco, tratamos de perfeccionar depurando los defenctos de aquellas más viejas con estas otras más nuevas que llevan incorporados nuevos parámetros despuñés descubiertos.
¿Por qué, pues, la Ciencia tiene éxito? La respuesta es que nadie lo sabe. Es un completo misterio-quizá el completo misterio- por qué la mente humana puede comprender algo del vasto universo. Como solía decir Einstein “Lo más incomprensible del universo es que lo podamos comprender”.
éxito? La respuesta es que nadie lo sabe. Es un completo misterio-quizá el completo misterio- por qué la mente humana puede comprender algo del vasto universo. Como solía decir Einstein “Lo más incomprensible del universo es que lo podamos comprender”.

Quizá como nuestro cerebro evoluciona mediante la acción de las leyes naturales, éstas resuenan y vibran de alguna manera, por nosotros desconocida en él. La Naturaleza nos presenta una serie de repeticiones -pautas de conducta que reaparecen a escalas diferentes, haciendo posible identificar principios, como las leyes de conservación, que se aplican de moso universal- y estas pueden proporcionar el vínculo entre lo que ocurre dentro y fuera de nuestras mentes. Pero, el misterio, realmente no es que coincidamos de alguna manera con el universo, sino que en cierta medida estamos en conflicto con él, y sin embargo podemos comprender algo de él. ¿Por qué esto es asó? Sin lugar a ninguna duda es por el simple hecho de que somos “una parte del universo” ¡La que piensa! y, al estar a él conectados con esos hilos invisbles de la Mente, nos llegan mensajes que despiertan la intuición que nos lleva de la mano de los nuevos pensamientos que surgen hacia ese mundo mágico del saber.
del universo” ¡La que piensa! y, al estar a él conectados con esos hilos invisbles de la Mente, nos llegan mensajes que despiertan la intuición que nos lleva de la mano de los nuevos pensamientos que surgen hacia ese mundo mágico del saber.
Claro que, el teorema de Gódel indica que siempre estaremos limitados en el saber del universo u, esos limites subyacen, muy posiblemente en aquella ruptura de las simetrías cósmicas en el momento de la génesis o de lo que fuera lo que allí pasó, si fluctuación de vacío, a un cambio de fase especatacular que, desde otro iniverso, nos envió a éste nuestro creado en la transición.
otro iniverso, nos envió a éste nuestro creado en la transición.
Ningún hombre, o mujer, realmente reflexivo deberían desear saberlo todo. Es precisamente el no saber lo que nos hace seguir buscando. Siempre he dicho que son muchas más las preguntas que las respuestas.
¡Sabemos tan poco! De hecho, ni sabemos de donde venimos y hacia donde vamos, lo que, por otra parte, nos ofrece un gran campo para la especulación de mlo que fue y de lo que podría ser.
emilio silvera
















 Totales: 75.420.028
Totales: 75.420.028 Conectados: 28
Conectados: 28























