¡Preludio a la relatividad! -Las ecuaciones de Lorentz-Fitzgerald- Éste último pensaba y decía cosas comos estas:

          George FitzGerald

“… la telegrafía debe mucho a Euclides y otros geómetras puros, al griego y al árabe que fueron matemáticos magistrales que inventaron nuestra escala de numeración y el álgebra, de Galileo y Newton, que fundaron la dinámica, para que Newton y Leibniz inventaran el cálculo, para que Volta descubriera la galvánica bobina, a Oersted quien descubrió la acción magnética de las corrientes, que a Ampère descubriera las leyes de su acción, a Ohm que descubrió la ley de la resistencia de los cables, a Wheatstone, de Faraday, a Lord Kelvin, a Clerk Maxwell, Hertz a… Sin los descubrimientos, invenciones, y las teorías científicas resumen de estos hombres la telegrafía y otras maravillas y conocimientos…  ¡serían imposibles ahora!”

    Hendrik Antoon Lorentz

Se le deben importantes aportaciones en los campos de la termodinámica, la radiación, el magnetismo, la electricidad y la refracción de la luz.  Formuló conjuntamente con George Francis FitzGerald una teoría sobre el cambio de forma de un cuerpo como resultado de su movimiento; este efecto, conocido como “contracción de Lorentz-FitzGerald”, cuya representación matemática de ella es conocida con el de transformación de Lorentz,  fue una más de las numerosas contribuciones realizadas por Lorentz al desarrollo de la teoría de la relatividad.

Fue, al igual que Henri Poincaré,  uno de los primeros en formular las bases de la teoría de la relatividad (frecuentemente atribuida primaria o solamente a Albert Einstein).  Fue ganador del Premio Nobel de Física en 1902, junto con su pupilo Pieter Zeeman,  por su investigación conjunta sobre la influencia del magnetismo en la radiación, originando la radiación electromagnética.  fue premiado con la Medalla Rumford en 1908 y la Medalla Coplay en 1918. Lorentz era hombre humilde y sencillo y le gustaba resaltar los logros de los demás:

                   Michael Faraday

“Como es probable que sepas, gran parte de nuestro conocimiento sobre la electricidad y el magnetismo se basa en los experimentos ingeniosísimos realizados por Michael Faraday en la primera parte del siglo XIX. Faraday era un experimentador genial, y descubrió numerosos fenómenos desconocidos hasta entonces, como la mutua. Estableció diversas leyes, pero no pudo elaborar una teoría global acerca del electromagnetismo porque sus conocimientos matemáticos no iban más allá de la trigonometría: hacía falta un teórico capaz de amalgamar el conocimiento adquirido por Faraday y otros experimentadores, como Hans Christian Ørsted, en una teoría general”.

Ese teórico era otro genio, James Clerk Maxwell, que estableció un conjunto de cuatro ecuaciones diferenciales bellísimas que describían de una manera extraordinariamente precisa los resultados de casi todos los experimentos de Faraday, Ørsted y compañía. Lo más sorprendente, el propio Maxwell y sus contemporáneos, fue una de las consecuencias inevitables de sus ecuaciones: la existencia de perturbaciones del campo eléctrico y el magnético que se propagaban por el espacio.”

A la contracción, Einstein le dio un marco teórico en la teoría especial de la relatividad. En teoría, un objeto de longitud l₀ en reposo en un sistema de referencia parecerá, un observador en otro sistema de referencia que se mueve con velocidad relativa v con respecto al primero, tener longitud , donde c es la velocidad de la luz. La hipótesis original atribuía contracción a una contracción real que acompaña al movimiento absoluto del cuerpo. La contracción es en cualquier caso despreciable a no ser que v sea del mismo orden o cercana a c.

             Si no alcanza esa velocidad, nunca podrá escapar de la Gravedad de la Tierra

Un objeto que se moviera a 11,2 Km/s (la velocidad de escape de nuestro planeta) experimentaría sólo una contracción equivalente a 2 partes por cada 1.000 millones en el sentido del vuelo. Pero a velocidades realmente elevadas, tal contracción sería sustancial. A unos 150.000 Km/s (la mitad de la velocidad de la luz) sería del 15%; a 262.000 Km/s (7/8 de la velocidad de la luz), del 50%. Es decir, que una regla de 30 cm que pasara ante nuestra vista a 262.000 Km/s nos parecería que mide sólo 15’24 cm, siempre y cuando conociéramos alguna manera para medir su longitud en pleno vuelo. Y a la velocidad de la luz, es decir, 300.000 Km/s en números redondos, su longitud en la dirección del movimiento sería cero. Puesto que, presuntamente, no puede existir ninguna longitud inferior a cero, se deduce que la velocidad de la luz en el vacío es la mayor que puede imaginarse el universo.

                                                                                 experimento conocido de Michelson-Morley

Todo aquello fue posible gracia a que en 1893, el físico irlandés George Francis FitzGerald emitió una hipótesis explicar los resultados negativos del experimento conocido de Michelson-Morley.  Adujo que toda materia se contrae en la dirección del movimiento, y que esa contracción es directamente proporcional al ritmo (velocidad) del movimiento.

Según tal interpretación, el interferómetro se quedaba corto en la dirección del “verdadero” movimiento terrestre, y lo hacía precisamente en una cantidad que compensaba con toda exactitud la diferencia de distancias que debería recorrer el rayo luminoso.  Por añadidura, todos los aparatos medidores imaginables, incluyendo los órganos sensoriales humanos, experimentarían ese mismo fenómeno.

Parecía como si la explicación de FitzGerald insinuara que la Naturaleza conspiraba con objeto de impedir que el hombre midiera el movimiento absoluto, lo cual introducía un efecto que anulaba cualquier diferencia aprovechable para detectar dicho movimiento.

Este asombroso fenómeno recibió el de “contracción de FitzGerald”, y su autor formuló una ecuación para el mismo que, referido a la contracción de un cuerpo móvil, fue predicha igualmente, y de manera independiente, por H.A.Lorentz (1853-1928) de manera que, finalmente, se quedaron unidas como “Contracción de Lorentz-Fitz Gerald”.

El efecto Fitzgerald sobre longitudes y el efecto Lorentz sobre masas mantuvieron una conexión tan estrecha que aparecieron a menudo agrupadas como las ecuaciones Lorentz-Fitzgerald.

La dilatación del tiempo es el fenómeno predicho por la teorçia de la relatividad,  por el cual un observador observa que el reloj de otro (un reloj físicamente idéntico al suyo) está marcando el tiempo a un ritmo menor que el que mide su reloj. Esto se suele interpretar normalmente como que el tiempo se ha ralentizado para el otro reloj, pero eso es cierto solamente en el contexto del sistema de referencia del observador. Localmente, el tiempo siempre está pasando al mismo ritmo. El fenómeno de la dilatación del tiempo se aplica a cualquier proceso que manifieste cambios a través del tiempo.

Donde:

es el intervalo temporal entre dos eventos co-locales para un observador en algún sistema de referencia inercial. (por ejemplo el número de tic tacs que ha hecho su reloj)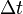

es el intervalo temporal entre los dos mismos eventos, tal y como lo mediría otro observador moviéndose inercialmente con velocidad v, respecto al primer observador

es la velocidad relativa entre los dos observadores

la velocidad de la luz y

es el también conocido como factor de Lorentz

De esta manera la duración del un ciclo de reloj del reloj que se mueve se ha incrementado: esta “funcionando más despacio”. Según lo indicado las transformaciones de Lorentz  pueden ser utilizadas para casos más generales.

Postulados de la Relatividad Especial

• Primer postulado:  Principio especial de relatividad: Las leyes de la física son las mismas en todos los sistemas de referencia inerciales. En otras palabras, no existe un sistema inercial de referencia privilegiado, que se pueda considerar como absoluto.

• Segundo postulado: Invariancia de c: La velocidad de la luz en el vacío es una constante universal, c, que es independiente del movimiento de la fuente de luz.

Hace 66 millones de años, una roca espacial de 10 kilómetros chocó contra la Tierra causando una explosión equivalente a 7.000 millones de bombas atómicas. El choque levantó una enorme fumarola de roca pulverizada que se elevó hasta cubrir todo el globo y sumirlo en una profunda oscuridad. Tsunamis de más de 100 metros arrasaron las costas del actual Golfo de México, donde cayó el meteorito, y se desencadenaron fuertes terremotos. Parte de los escombros levantados por el impacto comenzaron a llover como diminutos meteoritos y transformaron el planeta en un infierno de bosques ardiendo. Las plantas que no se quemaron se quedaron sin luz solar durante meses. Tres de cada cuatro seres vivos en el planeta fueron exterminados, incluidos todos los dinosaurios no avianos.

Una de las grandes incógnitas sobre el evento de extinción masiva del Cretácico es si existió un refugio donde la vida permaneció más o menos intacta. Algunos estudios han situado ese oasis en el hemisferio sur del planeta, especialmente cerca del Polo.

“La mayoría de lo que sabemos sobre la extinción y la recuperación de la vida en tierra después del asteroide viene del Oeste de EE UU, relativamente cerca del lugar del impacto, en Chixculub, México”, explica Michael Donovan, investigador de la Universidad estatal de Pensilvania (EE UU). Se sabe “mucho menos” de lo que sucedió en otras zonas más alejadas, dice, pero hay estudios recientes del polen y las esporas que apuntan a que en Patagonia y Nueva Zelanda la extinción de plantas fue mucho menor.

En un estudio publicado hoy en Nature Ecology & Evolution, Donovan y otros científicos en EE UU, Argentina y China exploran la hipótesis del refugio del sur a través del análisis de hojas fósiles de antes y después del impacto encontradas en la Patagonia argentina. En concreto, el equipo de investigadores ha analizado las pequeñas mordeduras dejadas por insectos herbívoros en la vegetación para estimar cuándo se recuperó el nivel de diversidad biológica anterior al desastre.

Los resultados muestran que, al igual que lo que se observó en el hemisferio norte, los insectos del sur prácticamente desaparecieron después del choque del meteorito. Pero los fósiles analizados también muestran que los niveles de diversidad de insectos se recuperaron en unos cuatro millones de años, dos veces más rápido que en el norte.

“También hemos estudiado los minadores, rastros de deterioro en las hojas hechos por larvas de insecto al alimentarse”, explica Donovan. “No encontramos pruebas de la supervivencia de minadores del Cretácico, lo que sugiere que este no fue un refugio para estos insectos”, explica, pero en los restos de después del impacto enseguida aparecen nuevas especies.

El trabajo refuerza la hipótesis de que la vida regresó antes a las zonas más alejadas del punto de impacto, “aunque también pudo haber otros factores desconocidos”, advierte Donovan. Las diferencias en el tiempo de recuperación probablemente influyeron en los patrones de biodiversidad hasta la actualidad, comenta.

El trabajo también puede ayudar a explicar por qué otras pequeñas criaturas que se alimentaban de insectos acabaron conquistando la Tierra tras sobrevivir al meteorito que exterminó a los dinosaurios. “Es posible que los cambios en la cadena alimentaria causados por la extinción de los insectos después del impacto, seguidos de la recuperación de los niveles anteriores afectasen a otros organismos, incluidos los mamíferos”, resalta.

El 24 de febrero de 1987, desde el observatorio chileno de Las Campanas se detectó un intenso brillo en el cielo. Era una supernova producida por el estallido de una estrella que había agotado su combustible. El cataclismo se había producido a las afueras de la Nebulosa de la Tarántula, en la Gran Nube de Magallanes, una galaxia enana situada en el vecindario de nuestra Vía Láctea. Este fenómeno, que solo se produce en nuestro entorno galáctico tres o cuatro veces cada siglo, permitió además detectar los primeros neutrinos procedentes de fuera del Sistema Solar. La captura de esos neutrinos extrasolares se produjo en el observatorio japonés Kamiokande. Aunque eran solo 24, proporcionaron gran cantidad de información sobre la supernova e hicieron merecedor del Nobel de física Masatoshi Koshiba.

Los neutrinos son unas partículas sin carga eléctrica que interactúan muy poco con el resto de la materia y pueden viajar por el cosmos sin verse afectados por los campos magnéticos que desvían otro tipo de partículas. Eso hace fácil determinar su origen y les convierte en buenos mensajeros para estudiar violentos fenómenos como las supernovas o los agujeros negros. El observatorio de Kamioka, construido en una mina a un kilómetro bajo tierra a principios de los 80, fue sustituido por una versión mejorada del experimento. Un gran tanque de 45 metros de diámetro por 45 metros metros de altura, lleno con 50.000 toneladas de agua pura, sirvió como trampa para atrapar estas escurridizas partículas.

Ahora, según adelantaba la Agencia Sinc esta semana, los miembros de la colaboración internacional de científicos que trabaja en Super-Kamiokande han desarrollado un sistema de vigilancia para estar listo en caso de que estalle una supernova y poder detectarla. Según explica Luis Labarga, investigador de la Universidad Autónoma de Madrid y uno de los autores del artículo que explica el plan en la revista Astroparticle Physics, “se trata de un sistema informático que está analizando constantemente los datos que va recogiendo el detector para ver si hay algún tipo de exceso de flujo, de sucesos, que permita obtener una pequeña estimación probabilística de si es o no una supernova”. “La idea es poder saber si ha ocurrido una supernova en las siguientes horas o minutos a que suceda”, añade.

En caso de que la respuesta de esta alerta temprana sea positiva, se enviaría un aviso a observatorios de todo el mundo con las coordenadas del lugar del cielo en el que ha ocurrido para que puedan estudiar el fenómeno. “La ventaja de Super-Kamiokande es que si existe una supernova galáctica lo va a ver siempre porque no está mirando a ningún lado. Los telescopios ópticos, sí”, apunta Labarga.

Cuando estalla una supernova, la mayor parte de la energía que se libera lo hace en forma de neutrinos. Por eso, los estudiar estas partículas puede ayudar a entender bien estos fenómenos. Algunos de los objetos que se pueden estudiar mejor gracias a este nuevo tipo de astrofísica son las estrellas de neutrones y los agujeros negros, monstruos de materia superconcentrada que aparecen cuando las estrellas se colapsan bajo su propia gravedad.

Uno de los misterios que han rodeado a la supernova detectada en 1987 procede de la imposibilidad de detectar la estrella de neutrones que debería haber quedado tras el estallido de la estrella original. Algunas hipótesis para explicar la ausencia de esa estrella apuntan a que podría haber acumulado materia suficiente para producir un nuevo colapso y acabar convertida en un agujero negro. Gigantescas trampas para neutrinos como la japonesa de Kamioka pueden ayudar a resolver este y otros enigmas.