Ago
11
Distancias inalcanzables (en el presente)
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Las distancias en el Espacio ~
Clasificado en Las distancias en el Espacio ~
 Comments (1)
Comments (1)
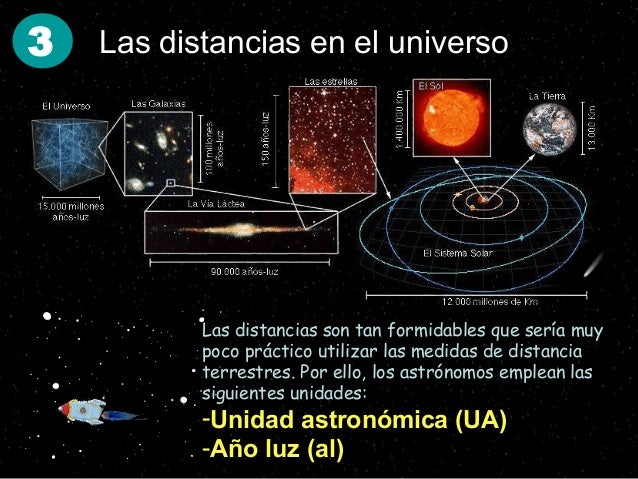
En el espacio exterior, el Cosmos, lo que conocemos por universo, las distancias son tan enormes que se tienen que medir con unidades espaciales como el año luz (distancia que recorre la luz en un año a razón de 299.792.458 metros por segundo). Otra unidad ya mayor es el pársec (pc), unidad básica de distancia estelar correspondiente a una paralaje trigonométrica de un segundo de arco (1”). En otras palabras, es la distancia a la que una Unidad Astronómica (UA = 150.000.000 Km) subtiende un ángulo de un segundo de arco. Un pársec es igual a 3’2616 años luz, o 206.265 Unidades Astronómicas, o 30’857×1012Km. Para las distancias a escalas galácticas o intergalácticas se emplea una unidad de medida superior al pársec, el kilopársec (Kpc) y el megapársec (Mpc).
Para tener una idea aproximada de estas distancias, pongamos el ejemplo de nuestra galaxia hermana, Andrómeda, situada (según el cuadro anterior a 725 kilopársec de nosotros) en el Grupo local a 2’3 millones de años luz de la Vía Láctea.
¿Nos mareamos un poco?
| 1 segundo luz | 299.792’458 Km |
| 1 minuto luz | 18.000.000 Km |
| 1 hora luz | 1.080.000.000 Km |
| 1 día luz. | 25.920.000.000 Km |
| 1 año luz | 9.460.800.000.000 Km |
| 2’3 millones de años luz | 21.759.840.000.000.000.000 Km |
¡Una barbaridad! Si tomamos conciencia de lo que realmente suponen estas distancias, y, pensamos que nuestras naves actuales podrían recorrer el Espacio a una velocidad máxima de unos 60.000 Km/h, nos podríamos preguntar cuanto tardaría una expedición en llegar a a un sistema planetario cercano, digamos que estuviera situado a unos 12 años luz . ¿Cuantas generaciones tendrían que morir en la nave hasta llegar al destino… ¡Si es que llegaba!?

Andrómeda, la hermana mayor de la Vía Láctea, situada a 2,3 años-luz de nosotros, viaja en nuestra dirección a una buena velocidad. Sin embargo, se calcula que nos no llegará hasta nosotros hasta dentro de unos pocos miles de millones de años, casi cuando el Sol tenga agotado su combustible nuclear de fusión, para convertirse en una Nebulosa planetaria con una enana blanca en su centro.

Ahí tenemos la imposibilidad física de viajar a otros mundos, y no digamos a otras galaxias. Las velocidades que pueden alcanzar en la actualidad nuestros ingenios espaciales no llegan ni a 50.000 Km/h. ¿Cuánto tardarían en recorrer los 21.759.840.000.000.000.000 Km que nos separa de Andrómeda?
Incluso el desplazarnos hasta la estrella más cercana, Alfa Centauri, resulta una tarea impensable si tenemos en cuenta que la distancia que nos separa es de 4’3 años luz, y un año luz = 9.460.800.000.000 Km. Así que, para llegar a la “cercana” Alfa Centauri tendríamos que multiplicar por 4 esa inmensa distancia. ¿Cuándo llegaríamos allí? ¿Los viajeros que partieron de la Tierra y muchas generaciones siguientes (si todo transcurre con normalidad) serían los que arribarían al destino. Sin embargo, dudo que, cuando llegaran, no hubieran padecido mutaciones por tan larga estancia en el Espacio.
Muchos son los que han querido imaginar como viajar más rápido que la Luz… ¡Sin superar su velocidad! Todos sabemos, como nos enseñó la Relatividad Especial de Einstein que, la luz, nos marca el límite de la velocidad que se puede alcanzar en el Espacio. Nada podrá nunca viajar más rápido que la luz en el vacío, es decir, más rápido de 299.792.458 metros cada segundo. Y, se idean otras formas para poder burlar ese límite y llegar antes que la luz a un determinado lugar. Hasta que no se busque la manera de esquivar la barrera de la velocidad de la luz, los viajes a otros mundos están algo complicados para nosotros.
La única ventaja a nuestro favor: ¡EL TIEMPO! Tenemos mucho, mucho tiempo por delante para conseguir descifrar los secretos del hiperespacio que nos mostrará otros caminos para desplazarnos por las estrella que, en definitiva, será el destino de la humanidad.

Nuestro Sol, antes de que pasen 4.000 millones de años, comenzará una transición de fase que, de estrella en la secuencia principal de HP, pasará a su fase terminal convirtiéndose en una Gigante roja que, eyectará sus capas exteriores al espacio interestelar formando una Nebulosa planetaria y, la estrella, exenta de la energía de fusión, quedará a merced de la fuerza de Gravedad que la comprimirá hasta límites de una densidad que sólo podrá ser frenada por la degeneración de los electrones. En ese punto, volverá el equilibrio entre dos fuerzas y el proceso se parará dejando una enana blanca con un radio parecido al de la Tierra y una densidad de 109 Kg m3.
Colisión Vía Láctea-Andrómeda – Wikipedia
Antes de que todo eso llegue, tenemos que tener en cuenta que habrá que salvar otro gran escollo que se nos viene encima (nunca mejor dicho), ya que, la Galaxia Andrómeda viene hacia La Vía Láctea a razón de 1.000.000 de Km/h y, aproximadamente en unos 3.000 millones de años la tendremos, irremediablemente, colisionando con nuestra Galaxia, con lo cual, las fuerzas de marea que esas enormes masas puden producir, son de impensable magnitud y, el desenlace tardará varios millones de años en finalizar hasta que de las dos grandes Galaxias del Grupo Local, sólo quede una enorme galaxia elíptica y, en el proceso, habrán nacido un sin fin de nuevas estrellas, otras habrán sido despladas de su regiones y lanzadas a distancias enormes, algunas habrán podido colisionar y, en definitiva, lo que allí pueda ocurrir en el futuro lejano, es de incalculable trascendencia para la Humanidad (si aún sigue aquí para ese tiempo).


Sí, existen muchos lugares a los que, cuando llegue el momento podremos viajar. Sin embargo, necesitamos muchos más conocimientos de los que actualmente tenemos para poder realizar esos viajes “imposibles” en las actuales circunstancias. Estamos comenzando, ahora, a poder realizar los primeros intentos de salir al Espacio, y, para cuando realmente podamos efectuar viajes espaciales, habrán pasado muchos, muchos, muchísimos años. No quiero mencionar, lo que podríamos tardar en dominar viajes hiperespaciales a velocidades uperlumínicas. Claro que, la imaginación humana es… ¡”infinita”!
Si esto es así (que lo es), tenemos una buena excusa para pensar en posibles modos de escapar hacia otros mundos lejanos en los que poder asentar a la Humanidad lejos de esos acontecimientos de magnitud (para nosotros) infinita y contra los que nada podremos hacer, excepto, si podemos y buscamos el medio… huir a otros lugares más seguros.
Si, las distancias que nos separan de esos otros mundos parece una barrera difícil de franquear, y, sin embargo, tengo una gran esperanza puesta en que, la Humanidad, la inteligencia de los seres que la compone, y, sobre todo su imaginación, con el tiempo por delante tendrá la oportunidad de buscar esas difíciles soluciones que posibiliten nuestro traslado a las estrellas lejanas.

Para lograr eso, con nuestras limitaciones actuales, no tenemos más remedio que valernos de sondas robotizadas y, en el futuro, serán perfectos robots humanoides que, no tendrán ninguna de nuestras barreras para deambular por el cielo y visitar esas regiones lejanas en las que, posiblemente, se encuentren los planetas idóneos para habitats de seres como nosotros.
Esas son, en realidad, las miras que están puestas en todas esas misiones enviadas a las lunas y planetas cercanos para estudiar su entorno, la atmósfera, la superficie y las radiaciones. Se trata de ir conociendo el entorno y, con los adelantos tecnológicos que ahora mismo tenemos, se hace lo que se va pudiendo y, cada día, se avanza un paso más a la búsqueda de esas soluciones que, ese día muy lejano aún, llegará la debacle a la Tierra y, para entonces, no podremos continuar aquí. La única solución: Escapar a otros mundos.
emilio silvera
Ago
11
Surgieron pensamientos… ¡Que nunca dejaran de asombrarnos!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (2)
Comments (2)

Ludwig Boltzmann será el protagonista de hoy
Hay ecuaciones que son aparentemente insignificantes por su reducido número de exponentes que, sin embargo, ¡dicen tántas cosas…! En la mente de todos están las sencillas ecuaciones de Einstein y de Planck sobre la energía-masa y la radiación de cuerpo negro. Esa es la belleza de la que hablan los físicos cuando se refieren a “ecuaciones bellas”.

Maxwell

Las ecuaciones de Maxwell…, “y se hizo la luz”
La identidad de Euler: Algunos dijeron de su ecuación: “la expresión matemática más profunda jamás escrita”, “misteriosa y sublime”, “llena de belleza cósmica”, “una explosión cerebral”.

Newton y su segunda ley que, aunque no funcione cuando nos acercamos a velocidades relativistas, rompió la marcha hacia la Gravedad.

Pitágoras y “su” teorema, también debe estar presente como lo está su teorema en las construcciones de todo el mundo y… mucho más.

Schrödinger y su función de onda que tampoco se queda atrás (aunque como la ecuación de Newton, si hablamos de velocidades relativistas…)
Bueno, E = mc2, nos lleva a profundidades de la materia antes jamás vistas y nos permite sacar conclusiones como que, en un gramo de materia está encerrada toda la energía consumida por la Humanidad durante un minuto. ¡Masa y Energía son la misma cosa!
Einstein, con esa ecuación de arriba de la relatividad general, vino a cambiar el mundo y, a partir de entonces, nació la verdadera cosmología. ¡Nos habla de tántas cosas!
¿Qué decir de la maravillosa fórmula de la entropía de Boltzman?
S = k log W
Creo que hoy, hablaremos de ella. Boltzman con su trabajo e ingenio, le dio a la Humanidad la herramienta para que pudiera seguir avanzando en el difícil laberinto de la Cienca, fue, sin duda, uno de los físicos más ilustres del siglo XIX.
El trabajo científico desarrollado por Boltzmann en su época crítica de transición que puso el colofón a la física “clásica” –cuya culminación podríamos situar en Maxwell– y antecedió (en pocos años) a la “nueva” física, que podemos decir que comenzó con Max Planck y Einstein. Aunque ciertamente no de la importancia de los dos últimos, la labor científica de Boltzmann tiene una gran relevancia, tanto por sus aportaciones directas (creador junto con “su amigo” Maxwell y Gibbs de la mecánica estadística, aunque sea el formulismo de éste último el que finalmente haya prevalecido; esclarecedor del significado de la entropía, etc.) como por la considerable influencia que tuvo en ilustres físicos posteriores a los que sus trabajos dieron la inspiración, como es el caso de los dos mencionados, Planck y Einstein.

Boltzmann fue un defensor a ultranza del atomismo, polemizando sobre todo con Mach y Ostwald, antiatomistas partidarios de la energética y claros exponentes de la corriente idealista de la física alemana. Tuvo que abandonar su ambiciosa idea de explicar exactamente la irreversibilidad en términos estrictamente mecánicos; pero esta “derrota”, no ocultaré que dolorosa desde el punto de vista personal, le fue finalmente muy productiva, pues de alguna manera fue lo que le llevó al concepto probabilista de la entropía. Estas primeras ideas de Boltzmann fueron reivindicadas y extendidas, en el contexto de la teoría de los sistemas dinámicos inestables, sobre todo por la escuela de Prigogine, a partir de la década de 1970.
La personalidad de Boltzmann era bastante compleja. Su estado de ánimo podía pasar de un desbordante optimismo al más negro pesimismo en cuestión de unas pocas horas. Era muy inquieto; él decía – medio en serio, medio en broma – que eso se debía a haber nacido en las bulliciosas horas finales de los alegres bailes del Martes de Carnaval, previas a los “duelos y quebrantos” (entonces) del Miércoles de Ceniza.

Ludwig Boltzmann and co-workers in Graz, 1887. (standing, from the left) Nernst, Streintz, Arrhenius, Hiecke, (sitting, from the left) Aulinger, Ettingshausen, Boltzmann, Klemenčič, Hausmanninger
Su lamentable final, su suicidio en Duino (Trieste) el 5 de septiembre de 1906, muy probablemente no fue ajeno a esa retorcida personalidad, aunque su precaria salud física fue seguramente determinante a la hora de dar el trágico paso hacia el lado oscuro.
Uno de los problemas conceptuales más importantes de la física es cómo hacer compatible la evolución irreversible de los sistemas macroscópicos (el segundo principio de la termodinámica) con la mecánica reversible (las ecuaciones de Hamilton o la ecuación de Schrödinger) de las partículas (átomos o moléculas) que las constituyen. Desde que Boltzmann dedujo su ecuación en 1872, este problema ha dado lugar a muy amplios debates, y el origen de la irreversibilidad es, aún hoy en día, controvertido.

En una de sus primeras publicaciones, Boltzmann obtuvo en 1866 una expresión de la entropía, que había sido definida un año antes por Clausius, basado en conceptos mecánicos. Las limitaciones de este trabajo eran que su aplicación se restringía al estudio de los gases y que el sistema era periódico en el tiempo. Además, Boltzmann no pudo deducir de su definición de entropía la irreversibilidad del segundo principio de la termodinámica de Clausius. En 1868, basándose en las ideas probabilísticas de Maxwell, obtuvo la distribución de equilibrio de un gas de partículas puntuales bajo la acción de una fuerza que deriva de un potencial (distribución de Maxwell-Boltzmann).

En el Universo, considerado como sistema cerrado, la entropía crece y…
En 1.872 publicó la denominada ecuación de Boltzmann para cuya deducción se basó, aparentemente, en ideas mecánicas. Esta ecuación contiene, sin embargo, una hipótesis no mecánica (estadística) o hipótesis del caos molecular, que Boltzmann no apreció como tal, y cuya mayor consecuencia es que, cualquiera que sea la distribución inicial de velocidad de un gas homogéneo diluido fuera del equilibrio, ésta evoluciona irreversiblemente hacia la distribución de velocidad de Maxwell. A raíz de las críticas de Loschmidt (paradoja de la reversibilidad) y Zermelo (paradoja de la recurrencia), Boltzmann acabó reconociendo el carácter estadístico de su hipótesis, y en 1877 propuso una relación entre la entropía Sde un sistema de energía constante y el número de estados dinámicos W accesibles al sistema en su espacio de fases; esto es, la conocida ecuación S = kB ln W, donde kB es la constante de Boltzmann. En esta nota, se hace una breve descripción de la ecuación de Boltzmann y de la hipótesis del caos molecular.

El comportamiento de los gases siempre dio a los físicos en qué pensar
La ecuación de Boltzmann describe la evolución temporal de un gas diluido de N partículas puntuales de masa m contenidas en un volumen V que interaccionan a través de un potencial de par central repulsivo V(r) de corto alcance a. Como simplificación adicional, considérese que sobre las partículas no actúan campos externos. Si f1(r,v,t) indica la densidad de partículas que en el tiempo t tienen un vector de posición r y velocidad v, que está normalizada en forma:
∫dr ∫dvƒ1(r,v,t) = N
Su evolución temporal es la suma de dos contribuciones. En ausencia de interacción, las partículas que en el tiempo t tienen vector de posición r y velocidad v se encuentran, después de un intervalo de tiempo Δt, en r + v Δt y tiene la misma velocidad. Como
f1(r + vΔt,v,t + Δt) = f1(r,v,t)
en el límite Δt → 0 (2) se escribe:
∂1 f1(r,v,t) = – v∂r f1(r,v,t)
Que es una ecuación invariante bajo el cambio t → – t y v → – v. La evolución es, por tanto, mecánica.
Se cumplieron más de cien años desde la muerte de Boltzmann y su trabajo sigue siendo recordado. No pienso que Boltzmann creyera en la existencia real de los átomos, pero sí en su utilidad e incluso en su necesidad para comprender las leyes macroscópicas y la evolución irreversible de los fenómenos macroscópicos desde una base más fundamental que el nivel fenomenológico. Pero había quien (con autoridad) no creía ni en la existencia ni en su utilidad. Este debate no era ajeno a las tendencias ideológicas, religiosas y usos sociales de aquella época porque, en general, la ciencia es parte de la cultura y depende del momento histórico que viven los científicos, al fin y al cabo, seres humanos como los demás, influenciables por su entorno en una gran medida.
Por el siglo XIX, e incluso antes, ya se hablaba de “átomos”* y una rudimentaria teoría cinética de los gases gozaba de aceptación y utilidad científica (recordemos los trabajos de Benoulli, Dalton, Laplace, Poisson, Cauchy, Clausius, Krönig… y Maxwell). Pero fue Boltzmann quien definitivamente profundizó en la cuestión, para el estudio del equilibrio y, sobre todo, intentando explicar mecánicamente (mecano-estadísticamente) la evolución termodinámica irreversible y la descripción de los procesos de transporte ligados a ella. Y, nuevamente (por su enorme importancia) no podemos dejar de mencionar la muy singular labor que hicieron Gibbs, Einstein, Planck, Fermi y otros. Sin la motivación ideológica de Boltzmann, Gibbs elaboró una bellísima, útil y hoy dominante formulación (cuerpo de doctrina) de la termodinámica y física estadística.
Lorentz
Fue Lorentz quien primero utilizó la ecuación de Boltzmann y lo hizo para describir la corriente eléctrica en sólidos dando un paso significativo por encima del pionero Drude. Lorentz introdujo un modelo opuesto al browniano donde partículas ligeras como viento (electrones) se mueven chocando entre sí y con árboles gordos (tales como iones en una red cristalina); un modelo del que se han hecho estudios de interés tanto físico como matemático. Enskog (inspirándose en Hilbert) y Chapman (inspirándose en Maxwell) enseñaron cómo integrar la ecuación de Boltzmann, abriendo vías a otras diversas aplicaciones (hidrodinámica, propagación del sonido, difusión másica, calor, fricción viscosa, termoelectricidad, etc.). Recordemos que Boltzmann encontró como solución de equilibrio de su ecuación una distribución de velocidades antes descubierta por Maxwell (hoy, como reseñé anteriormente, de Maxwell-Boltzmann), por lo que concluyó que así daba base microscópica mecánica (teorema H mecano-estadístico) al segundo principio de la termodinámica (estrictamente, evolución de un sistema aislado hacia su “desorden” máximo).
El físico austríaco Ludwig Boltzmann sentó las bases estadísticas de la entropía, su trabajo fue tan importante que el gran físico Max Planck sugirió que su versión de la fórmula de Boltzmann fuera grabada en la lápida de Boltzmann de Viena.
Está claro que ningún físico que se precie de serlo puede visitar Viena sin visitar el parque Zentralfriedhof para ver la tumba de Boltzmann. Yo sí me pasé por allí. Me senté junto a la tumba; el lugar estaba desierto, y cerrando los ojos traté de conectar con la conciencia del genio. La sensación, extraña y agradable, seguramente fue creada por mi imaginación, pero creo que charlé con él en el interior de mi mente – la fuerza más potente del universo– y aquellos sentimientos, aquel momento, compensaron el esfuerzo del viaje.
En la tumba, sobre una gran lápida de mármol de color blanco con los nombres Ludwig Boltzmann y de los familiares enterrados con él, sobre el busto de Boltzmann, se puede leer la inscripción, a modo de epitafio:
En esta breve ecuación se encierra la conexión entre el micromundo y el macromundo, y por ella se reconoce a Boltzmann como el padre de la rama de la física conocida como mecánica estadística. Esta sencilla ecuación es la mayor aportación de Boltzmann y una de las ecuaciones más importantes de la física. El significado de las tres letras que aparecen (aparte la notación del logaritmo) es el siguiente:
- S es la entropía de un sistema.
- W es el número de microestados posibles de sus partículas elementales.
- k es una constante de proporcionalidad que hoy recibe el nombre de Constante de Boltzmann, de valor 1’3805 × 10-23 J/K (si el logaritmo se toma en la base natural).
En definitiva, la ecuación describe la estrecha relación entre la entropía (S) y las miles de formas de partículas que en un sistema se pueden arreglar (k log W). La última parte es difícil. K es la constante de Boltzmann y W es el número de elementos microscópicos de un sistema (por ejemplo, el impulso y la posición de los átomos individuales de gas) en un sistema macroscópico en un estado de equilibrio (por ejemplo, el gas de sellado en una botella). Parece que la naturaleza ama el caos cuando empuja a los sistemas hacia el desequilibrio y Boltzmann le llamó entropía a este fenómeno.

Los pensamientos, como los paisajes del mundo para el viajero incansable, son inesperados y sorprendentes. Nunca se sabe lo que puede surgir de una Mente bien preparada e intuitiva.
Cuando profundizamos un poco en lo que el cerebro humano ha sido capaz de generar, los pensamientpos que ha llegado a generar bien sea en forma de ecuaciones matemáticas o expresados con palabras, no podemos dejar de sorprendernos y maravillarnos al ver que, ¡todo el universo parece estar dentro de nuestras mentes! ¿Qué secretos se encierran allí? ¿Cómo nos lleva a estos pensamientos tan profundos?
Como todas las ecuaciones sencilla de gran trascendencia en la física (como la famosa E = mc2), hay un antes y un después de su formulación: sus consecuencias son de un calado tan profundo que cambiaron la forma de entender el mundo, y en particular, de hacer física a partir de ellas. De hecho, la sutileza de la ecuación es tal que hoy, cien años después de la muerte de su creador, se siguen investigando sus nada triviales consecuencias. Creo que lo mismo ocurrirá con α = 2πe2/ħc que, en tan reducido espacio y con tan pocos símbolos, encierra los misterios del electromagnetismo (el electrón), de la constante de Planck(la mecánica cuántica), y de la luz (la relatividad de Einstein), todo ello enterrado profundamente en las entrañas de un número: 137.
Bueno, a pesar de todo lo anterior, Schrödinger nos decía:
“La actitud científica ha de ser reconstruida, la ciencia ha de rehacerse de nuevo”

¡Lo grande y lo pequeño! ¡Son tantos los secretos de la Naturaleza!
Siempre hemos tenido consciencia de que en física, había que buscar nuevos paradigmas, nuevos caminos que nos llevaran más lejos. Es bien conocida la anécdota de que a finales del siglo XIX un destacado físico de la época William Thomson (1824-1907) conocido como Lord Kelvin, se atrevió a decir que solo dos pequeñas “nubecillas” arrojaban sombras sobre el majestuoso panorama de conocimiento que había construido la física clásica desde Galileo y Newton hasta ese momento: el resultado del experimento de Michelson-Morley, el cual había fallado en detectar la existencia del supuesto éter luminífero; y la radiación del cuerpo negro, i.e la incapacidad de la teoría electromagnética clásica de predecir la distribución de la energía radiante emitida a diferentes frecuencias emitidas por un radiador idealizado llamado cuerpo negro. Lo que Lord Kelvin no puedo predecir es que al tratar de disipar esas dos “nubecillas”, la física se vería irremediablemente arrastrada a una nueva física: la física moderna fundada sobre dos revoluciones en ciernes: la revolución relativista y la revolución cuánticacon dos científicos como protagonistas: Planck y Albert Einstein. Sin embargo, ha pasado un siglo y seguimos con esas dos únicas guías para continuar el camino y, resultan insuficientes para llegar a la meta que… ¡Está tan lejos!
emilio silvera
Ago
11
¿Terminaremos sabiendo nuestro origen?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo y... ¿nosotros? ~
Clasificado en El Universo y... ¿nosotros? ~
 Comments (0)
Comments (0)
NATURE
Alesi, el pequeño ancestro de simios y humanos
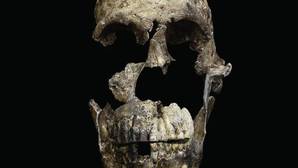
Un cráneo de 13 millones de años de antigüedad hallado en Kenia responde a interrogantes sobre los orígenes de la especie humana

Este cráneo, del tamaño de un limón, pertenece a una nueva especie Nyanzapithecus alesi – Fred Spoor
Científicos del Turkana Basin Institute de Kenia y del Anza College, en Estados Unidos, han descubierto en el yacimiento del lago Turkana a «Alesi», un cráneo completo que podría arrojar luz sobre el antepasado común de los actuales simios y humanos. Los restos, del tamaño de un limón, corresponden a una cría, de apenas un año y cuatro meses, de una especie recién bautizada que vivió hace 13 millones de años. Su nombre es «Nyanzapithecus alesi» y hace honor a la palabra «ales» que en turkano significa ancestro. El hallazgo se publicó ayer en la revista Nature.

«Nyanzapithecus alesi formaba parte de un grupo de primates que existió en África durante 10 millones de años», ha explicado Isaiah Nengo, investigador en la Universidad Stony Brook y primer autor del estudio. «Lo que muestra su descubrimiento es que este grupo estaba muy cerca del origen de los humanos y los simios actuales, y que este origen es africano».
El enigma de los ancestros
Entre todos los primates actuales, los humanos están más emparentados con los simios, que incluyen a chimpancés, gorilas, oranguntanes y gibones. Los fósiles muestran con claridad cómo hace siete millones de años, todos estos animales tenían un ancestro común, y cómo unos y otros evolucionaron desde entonces.

Sin embargo, los científicos saben poco sobre la evolución anterior de los ancestros de simios y humanos. ¿Qué pasó hace diez millones de años? Los fósiles que podrían explicarlo son muy escasos y apenas consisten en un puñado de dientes aislados y en pequeños fragmentos de mandíbulas. Por eso, por ejemplo, nunca se ha podido responder a la pregunta de si los ancestros de simios y humanos se originaron en África, o qué aspecto tenían. ¿Se parecían a los gibones? ¿O a animales mayores y más robustos?
Esta incertidumbre podría llegar a su fin, gracias a esta nueva investigación. Un cráneo fósil de simio del tamaño de un limón, el más completo hasta ahora de un simio extinto, y al que los investigadores han bautizado como Alesi, está llamado a ayudar a cerrar ese hueco crucial en la historia de los primates.
La historia de Alesi comienza en 2014, cuando fue hallado por un cazador de fósiles llamado John Ekusi. El pequeño estaba en el interior de una capa de sedimentos de 13 millones de años de antigüedad, situada en una región muy especial: en las cercanías de la zona de Napudet, una región situada al oeste del Lago Turkana, (al norte de Kenia), y famosa por haber brindado a los científicos innumerables fósiles con los que reconstruir los primeros pasos de la historia de la especie humana.
Enterrado por un volcán
«La zona de Napudet nos permite echar un vistazo único a un paisaje africano de hace 13 millones de años», ha explicado Craig S. Feibel, investigador de la Universidad Rutgers (Estados Unidos). «Un volcán próximo enterró el bosque donde vivía el pequeño simio, preservando los fósiles y muchos árboles. También nos proporcionó muchos minerales volcánicos cruciales para datar el fósil», ha añadido.
Aunque muchos de los interesantes rasgos de Alesi son visibles a simple vista, los investigadores lo han analizado también a través de una técnica de reconstrucción en tres dimensiones de altísima calidad y que es similar a una radiografía, en gran detalle. Estas pruebas se han realizado en el sofisticado Laboratorio Europeo de Radiación Sincrotrón de Grenoble, Francia.
Gracias a esto, han comprobado que el cráneo de Alesi es realmente extraordinario. «Fuimos capaces de reconstruir la cavidad cerebral, el oído interno y los dientes adultos, aún no emergidos, incluso con las líneas de crecimiento diarias», ha dicho Paul Tafforeau, investigador del laboratorio europeo. «La calidad de las imágenes era tan buena que averiguamos, gracias a los dientes, que la cría tenía un año y cuatro meses cuando murió».
Los dientes de una cría

Los dientes también han revelado otra información muy importante. Este pequeño simio pertenecía a una especie desconocida hasta ahora, y que los científicos han bautizado con el nombre de Nyanzapithecus alesi. «Hasta ahora, todas las especies del género «Nyanzapithecus eran conocida solo por sus dientes, y había muchos interrogantes abiertos sobre si eran simios o no», ha dicho John Fleagle, investigador de la Universidad Stony Brook. «Lo que aquí resulta crucial es que el cráneo tenía los canales óseos de los oídos totalmente desarrollados. Esto es un importante rasgo que vincula a este ejemplar con los simios actuales», ha resumido Ellen Miller, investigadora en la Universidad Wake Forest (Estados Unidos).
El cráneo de Alesi llama la atención por lo pequeño que es su hocico y por lo similar que resulta al de un gibón. Pero Alesi estaba emparentado con los simios actuales. Sus canales auditivos muestran que no se movía tan rápido como los gibones. Sus cautelosos movimientos le hicieron avanzar hacia la evolución de humanos y simios.
Ago
11
Otra confirmación de la Relatividad
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Relativista ~
Clasificado en Física Relativista ~
 Comments (0)
Comments (0)
CienciA-abc
Detectan pruebas de la Relatividad de Einstein en el monstruoso corazón de la Vía Láctea
Por primera vez, se han observado efectos relativistas en una estrella cercana a un agujero negro supermasivo.

La enorme masa de Sagitario A, el agujero negro supermasivo del centro de la galaxia, deforma el espacio-tiempo y desvía las órbitas de las estrellas – ESO/M. Parsa/L. Calçada
La Física que conocemos aún no ha podido adentrarse en los agujeros negros, pero sabemos perfectamente que están ahí. Uno de ellos ayuda a mantener unido ese vertiginoso remolino de cientos de miles de millones de estrellas que es la Vía Láctea. En su centro, a unos 26.000 años luz de la Tierra, «late» un agujero negro supermasivo de cuatro millones de masas solares y que recibe el nombre de Sagitario A (o también Sgr A*). No hace falta ser creyente para sentirse maravillado: Sagitario A es un gran atractor que mata estrellas y hace nacer a otras nuevas.
Los astrónomos están tratando de obtener la primera imagen de la historia de su horizonte de sucesos, ese límite predicho por Einstein y a partir del cual la Física se adentra en territorio desconocido. Pero mientras esto se logra, un equipo de científicos checos y alemanes se ha fijado en las estrellas de su entorno, durante 20 años, y han encontrado evidencias de efectos relativistas, predichos por Einstein un siglo atrás. Por primera vez, los astrónomos han detectado este tipo de efectos en estrellas que orbitan a alta velocidad el entorno de un agujero negro supermasivo.
Para poder mirar tan lejos los astrónomos han tenido que «viajar» hasta el Observatorio Paranal, en el desierto de Atacama, en Chile, del Observatorio Europeo Austral (ESO). Allí los cuatro telescopios ópticos del Very Large Telescope (VLT) les han permitido detectar los sutiles movimientos de las estrellas.

Si la Relatividad de Einstein funciona, como ya han demostrado otras muchas observaciones y experimentos, el movimiento de las estrellas cercanas al agujero negro no debería ser explicado solo a través de las leyes de Newton. La gravedad y las velocidades llevan a que sea la Relatividad la que explica su posición y movimiento.
Un laboratorio en el centro de la galaxia

«El centro de la galaxia es el mejor laboratorio para estudiar el movimiento de las estrellas en un entorno relativista», ha dicho Marzieh Parsa, investigadora en la Universidad de Colonia y primera autor del estudio. «Nos sorprendió cuán bien pudimos aplicar los métodos que desarrollamos con simulaciones para obtener datos de alta precisión sobre las estrellas que giran a alta velocidad y que están más cerca del agujero negro».
Esto es exactamente lo que ha ocurrido con una estrella bautizada con el poco sugerente nombre de S2. Gracias a la precisión del VLT, y de haber podido observarla cuando se acercaba y cuando se alejaba del agujero negro, los científicos han observado que la forma y la orientación de su órbita están influidas por efectos relativistas. Además, gracias a estas observaciones, los científicos han calculado con mayor exactitud la masa del agujero y su distancia hasta la Tierra.

En opinión de Vladimir Karas, investigador en la Academia de Ciencias de Praga, República Checa, «es muy alentador que S2 muestre comportamientos relativistas, tal como se esperaba en función de su proximidad a esas extrema concentración de masa en el centro de la Vía Láctea». Según él, estas observaciones abren un nuevo camino para nueas teorías y experimentos en este sector de la ciencia.
Esta historia continuará muy pronto. En 2018, la estrella S2 se acercará de nuevo al agujero negro supermasivo. Por entonces, un nuevo instrumento del VLT, el GRAVITY, permitirá medir su órbita con mayor precisión. Antes de que entren en funcionamiento la próxima generación de telescopios monstruosos, los astrónomos podrá medir con increíble exactitud los efectos relativistas en torno al centro de la Vía Láctea, o, por qué no, posibles desviaciones que ayuden a fundar una nueva Física, capaz de adentrarse en lo desconocido.
















 Totales: 75.601.185
Totales: 75.601.185 Conectados: 48
Conectados: 48






















