No siempre la Física se puede explicar con palabras

Se dice que un agujero negro (una masa M concentrada en un volumen menor que el dictado por su radio de Schwarzschild r_s = 2GM/c²) absorbe todo lo que cae sobre él. Sin embargo, Beckenstein y Hawking determinaron que el agujero negro posee entropía (proporcional al área del horizonte) y por ello temperatura, y Hawking concluye (1975) que la temperatura le hace radiar como un cuerpo negro; por tanto, eventualmente el agujero se evapora.

Aquí viene la paradoja. Si formamos el agujero negro arrojando materia en forma concreta (por ejemplo, un camión), la masa del camión acabaría eventualmente escupida como radiación del cuerpo negro, perdiéndose la preciosa información sobre el camión. Pero se supone que la evolución de “todo” es cuántica, y por ello unitaria. Ahora bien, la evolución unitaria mantiene la información (estados puros van a estados puros, no mezcla…); he ahí la paradoja.

                    Estaría bien poder entrar en un agujero negro para recabar información

Fue Hawking quien primero presentó la paradoja de “pérdida de información” en contra de otros que, como Gerard’t Hooft y Susskind, quienes mantienen que la información no se puede perder, y que por ello debe haber sutiles correlaciones en la radiación emitida, de las que en principio sería posible extraer la información original sobre que el agujero negro tragó un camión…

Paradogicamente, ha sido, durante el desarrollo de la “Teoría de Cuerdas” cuando se ha podido dilucidar el problema planteado hace veinticinco años por Beckenstein y Hawking que, han resultado llevar razón.

Recientemente S. Hawking ha cambiado de opinión y admite ahora que no hay pérdida de información, al respetarse el sentido unitario de la evolución del sistema, de acuerdo con la mecánica cuántica.

La gravitación y dimensiones extra

Esas hipotéticas dimensiones extra, necesarias para la existencia de la teoría de cuerdas, muchas las están buscando pero, de momento, nadie las pudo encontrar. Claro que, como para todo en este mundo, se necesita…¡Tiempo! dejemos que transcurra y…¡veremos!

“… la línea tiene magnitud en una dirección, el plano en dos direcciones y el sólido en tres direcciones; a parte de éstas, no hay ninguna magnitud porque las tres son todas…”

 

 

 

En nuestro Universo sólo podemos ver tres dimensiones y la temporal

 

Eso nos dijo Aristóteles alrededor de 350 años antes de Cristo, y la verdad, es que desde la experiencia cotidiana es difícil refutarlo. Más aún, la existencia de dimensiones extra podría tener consecuencias desastrosas para la estabilidad de las órbitas atómicas y planetarias, sobre todo en el caso de que dichas dimensiones fuesen de un tamaño comparable al del sistema estudiado. En concreto, Paul Ehrenfest en 1917 demostró que la ley del inverso del cuadrado de la distancia para la fuerza electrostática o gravitatoria se modificaría si hubiera N dimensiones espacial extra, de forma que F ≈ r^-2 π. De hecho, ningún experimentado físico realizado hasta la fecha ha revelado la existencia de más de tres dimensiones espaciales, y dicho sea de paso, tampoco más de una dimensión temporal.

Sin embargo, aunque la experiencia ordinaria no necesitase de más de tres más una dimensiones, desde Riemann, Gauss, Ricci y algún otro, el punto de vista matemático permite estudiar de forma consistente la geometría de espacion de dimensión arbitraria que, como digo, lo debemos en gran parte a Bernhard Riemann sobre variedades n-dimensionales (1854), y ello a pesar de que Ptolomeo propusiera una “demostración” de que una cuarta dimensión espacial no tiene magnitud ni definición posibles (Tratado sobre la distancia, 150 a. C.).

La formulación de la Relatividad Especial de Einstein en 1905 supuso una revolución en nuestra concepción del espacio y del tiempo, y planteó la cuestión de la dimensionalidad desde una perspectiva completamente nueva. En efecto, en la interpretación geométrica que llevó a cabo Herman Minkowski en 1909, la teoría de Einstein podía entenderse de forma simple en términos de una variedad espacio-temporal de cuatro dimensiones, en la que a tres dimensiones espaciales se le añadía en pie de igualdad una cuarta, el tiempo, en la forma itc. El espacio y el tiempo pasaron de entenderse como conceptos independientes a formar un entramado único 4-dimensional, en el que las distancias se miden a través de la métrica de Minkowski:

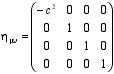
Por su parte, Einstein, lejos de considerar el espacio-tiempo de Minkowski como una mera descripción matemática, lo elevó a la categoría de entidad física con su Teoría General de la Relatividad (RG) de 1.915 al considerarlo como objeto dinámico, cuya geometría, dada por la métrica de Riemann g_μυ(x), depende de tener en cuenta en cada punto de su contenido de materia y energía. La curvatura del espacio-tiempo determina la trayectoria de las partículas de prueba que se mueven en él, y por tanto, la teoría proporciona una interpretación geométrica de la interacción gravitatoria.

La unificación del electromagnetismo y la gravitación, mencionada por mí en anteriores trabajos, fue la primera de las teorías con dimensiones extra. Se la envi´ço un oscuro matemático desconocido a Einstein, en una carta manuscrita en la que, le presentaba la teoría de 5 dimensiones en la que, era posible unificar, las dos teorías más grandes del momento (relatividad y electromagnetismo). Einsten la leyó varias veces y la volvía a guardad y, por fin, después de dos años, se decidió a enviarla para su publicación. Allí nació la teoría primera de más altas dimensiones: la de Kaluza-Klein (este último la mejoró más tarde).

Está claro que a comienzos del siglo pasado, nuestro conocimiento de las interacciones fundamentales se reducía a dos teorías de campos bien establecidas, el electromagnetismo de Maxwell, en pie desde 1873, y la novedosa Teoría General de la Relatividad para la gravitación, que Einstein comenzara a gestar en 1907 y publicara en 1915. No es por tanto de extrañar que el atractivo de la teoría de Einstein provocara en muchos, incluido el propio Einstein, el impulso de buscar una generalización de la misma, que incluyera también a la teoría de Maxwell, en una descripción geométrica unificada.

Con ese único objetivo, se tomaron varios caminos que, si bien no llegaron al destino deseado, permitieron realizar descubrimientos trascendentales que marcaría la evolución de la física teórica hasta nuestros días. (En aquellos tiempos se desconocían las fuerzaas nucleares débil y fuerte).

Se representan en este esquema dos partículas que se acercan entre sí siguiendo un movimiento acelerado. La interpretación newtoniana supone que el espacio-tiempo es llano y que lo que provoca la curvatura de las líneas de universo es la fuerza de interacción gravitatoria entre ambas partículas. Por el contrario, la interpretación einsteniana supone que las líneas de universo de estas partículas son geodésicas (“rectas”), y que es la propia curvatura del espacio tiempo lo que provoca su aproximación progresiva.

El primero de estos caminos fue propuesto por Hermann Weyl en 1918. En la Relatividad General, el espacio-tiempo se considera como una variedad pseudo-Riemanniana métrica, esto es, en la que, aunque la orientación de un vector transportado paralelamente de un punto a otro depende del camino seguido, su norma es independiente del transporte. Esta independencia de la norma disgustaba a Weyl que propuso reemplazar el tensor métrico g_μυ por una clase de métricas conformemente equivalentes [g_μυ] (esto es, equivalentes bajo cambios de escala g_μυ → λ g_μυ), y el transporte paralelo por otro que respetara esa estructura conforme. Esto se conseguía introduciendo un nuevo campo, A_μ, que al cambiar de representante de la clase de equivalencia [g_μυ], se transformaba precisamente como el potencial vector de la teoría de Maxwell:

A_μ → A_μ + ∂_μλ

               Hermann Weyl

Este tipo de transformación es lo que Weyl denominó trasformación de “gauge”, en el sentido de cambio de longitud. En propias palabras de Weyl en una carta dirigida a Einstein en 1.918, con su teoría había conseguido “… derivar la electricidad y la gravitación de una fuente común…“. La respuesta de Einstein no se hizo esperar:

“Aunque su idea es muy elegante, tengo que declarar francamente que, en mi opinión, es imposible que la teoría se corresponda con la naturaleza.”

 

La objeción de Einstein se basaba en el hecho de que en la propuesta de Weyl, el ritmo de avance de los relojes también dependería del camino seguido por éstos, lo cual entraría en contradicción, por ejemplo, con la estabilidad de los espectros atómicos.

Aunque la teoría de Weyl fue abandonada rápidamente, en ella se introducía por primera vez el concepto de simetría gauge. Varias décadas más tarde, con el desarrollo de las teorías gauge no abelianas por Yang Mills (1954), y del Modelo Estándar de las partículas elementales, se comprobó que la misma noción de invarianza subyacía en la descripción del resto de interacciones fundamentales (electrodébiles y fuertes).

La teoría de cinco dimensiones de Kaluza Klein fue la precursora de la de cuerdas

El segundo camino en la búsqueda de la unificación comenzó un año antes de la publicación de la Relatividad General. En 1914 Gunnar Nordström propuso una teoría en cinco dimensiones que unificaba el electromagnetismo con la gravitación de Newton. La aparición de la Teoría de la Relatividad General hizo olvidar la teoría de Nordström, pero no la idea de la unificación a través de dimensiones extra.

Kaluza

Así estaban las cosas cuando en 1.919 recibió Einstein un trabajo de Theodor Kaluza, un privatdozent*en la Universidad de Königsberg, en el que extendía la Relatividad General a cinco dimensiones. Kaluza consideraba un espacio con cuatro dimensiones, más la correspondiente dimensión temporal y suponía que la métrica del espacio-tiempo se podía escribir como:

Donde  con μ,υ = 1, 2, 3, 4, corresponde a la métrica 4-dimensional del espacio-tiempo de la RG, A_μproporciona el campo electromagnético, Φ es un campo escalar conocido posteriormente como dilatón, y α = √2k es la constante de acoplo relacionada con la constante de Newton k. Kaluza demostró que las ecuaciones de Einstein en cinco dimensiones obtenidas de esta métrica y linealizadas por los campos, se reducían a las ecuaciones de Einstein ordinarias (en cuatro dimensiones) en vacío, junto con las ecuaciones de Maxwell para A_μ, siempre que se impusiera la condición cilíndrica, esto es, que la métrica  no dependiera de la quinta coordenada.

El trabajo de Kaluza impresionó muy positivamente a Einstein: “Nunca había caído en la cuenta de lograr una teoría unificada por medio de un cilindro de cinco dimensiones… A primera vista, su idea me gusta enormemente…” (carta de Einstein a Kaluza en 1919, en abril).

Este hecho resulta sorprendente si consideramos que el trabajo de Nordström fue publicado cinco años antes. Por motivos desconocidos, en el mes de mayo de 1919, Einstein rebajó su entusiasmo inicial: “Respeto en gran medida la belleza y lo atrevido de su idea, pero comprenderá que a la vista de las objeciones actuales no pueda tomar parte como originalmente se planeó“. Einstein retuvo el trabajo de T. Kaluza durante dos años, hasta que en 1.921 fue presentado por él mismo ante la Academia Prusiana. Hasta 1.926 Einstein guardó silencia acerca de la teoría en cinco dimensiones.

Ese mismo año, Oskar Klein publicaba un trabajo sobre la relación entre la teoría cuántica y la relatividad en cinco dimensiones. Uno de los principales defectos del modelo de Kaluza era la interpretación física de la quinta dimensión. La condición cilíndrica impuesta ad hoc hacía que ningún campo dependiera de la dimensión extra, pero no se justificaba de manera alguna.

Klein propuso que los campos podrían depender de ella, pero que ésta tendría la topología de un círculo con un radio muy pequeño, lo cual garantizaría la cuantización de la carga eléctrica. Su diminuto tamaño, R₅ ≈ 8×10^{-31 cm}, cercano a la longitud de Planck, explicaría el hecho de que la dimensión extra no se observe en los experimentos ordinarios, y en particular, que la ley del inverso del cuadrado se cumpla para distancias r » R₅. Pero además, la condición de periodicidad implica que existe una isometría de la métrica bajo traslaciones en la quinta dimensión, cuyo grupo U(1), coincide con el grupo de simetría gauge del electromagnetismo.

Oskar Benjamin Klein (1894-1977). Fotografía tomada para el Göttingen Bohr-Festspiele, junio de 1922.

Por último, imponiendo que el dilaton es una constante, Klein demostró que las ecuaciones de movimiento reproducen las ecuaciones completas de Einstein y Maxwell. Esta forma de tratar la dimensión extra, bautizada posteriormente como el paradigma de la compactificación, había logrado superar los obstáculos iniciales: “… parece que la unión de la gravitación y la teoría de Maxwell se consigue de una forma completamente satisfactoria con la teoría de cinco dimensiones” (carta de Einstein a Lorentz en 1927), y de hecho, ha sido la única forma consistente de introducir dimensiones extra hasta fechas más recientes.

El propio Einstein había comenzado a trabajar en la teoría de Kaluza con su ayudante Jacob Grommer y en 1.922 publicó un primer trabajo sobre existencia de soluciones esféricamente simétricas, con resultado negativo. Más tarde, en 1927 presentó ante la Academia Prusiana dos trabajos en los que reobtenía los resultados de Klein. Su infructuosa búsqueda de una teoría de campo unificada le haría volver cada pocos años a la teoría en cinco dimensiones durante el resto de su vida. Los resultados de Klein sobre la cuantización de la carga eléctrica pueden entenderse fácilmente considerando el desarrollo en modos de Fourier de los campos con respecto a la dimensión periódica:

La ecuación de ondas en cinco dimensiones puede reescribirse como:

Donde D_μ es una derivada covariante con respecto a transformaciones generales de coordenadas y con respecto a transformaciones gauge con una carga q_n = nk/R₅. Vemos por tanto que el campo en cinco dimensiones se descompone en una torre infinita de modos 4-dimensionales Ψ_n(x) con masas , en unidades naturales ћ = c = 1, y carga q_n (modos de Kaluza-Klein).

Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck).  Si se duplica el valor de todas las masas no se puede llegar a saber, porque todos los números puros definidos por las razones de cualquier par de masas son invariables.

Puesto que el radio de compactificación es tan pequeño, el valor típico de las masas será muy elevado, cercano a la masa de Planck M_p = k^-12 = 1’2 × 10¹⁹ GeV*, y por tanto, a las energías accesibles hoy día (y previsiblemente, tampoco en un futuro cercano – qué más quisieran E. Witten y los perseguidores de las supercuerdas -), únicamente el modo cero n = 0 será relevante. Esto plantea un serio problema para la teoría, pues no contendría partículas ligeras cargadas como las que conocemos.

¿Y si llevamos a Kaluza-Klein a dimensiones superiores para unificar todas las interacciones?

La descripción de las interacciones débiles y fuertes a través de teorías gauge no abelianas mostró las limitaciones de los modelos en cinco dimensiones, pues éstas requerirían grupos de simetría mayores que el del electromagnetismo. En 1964 Bryce de UIT presentó el primer modelo de tipo Kaluza-Klein-Yang-Mills en el que el espacio extra contenía más de una dimensión.

El siguiente paso sería construir un modelo cuyo grupo de isometría contuviese el del Modelo Estándar SU(3)_c × SU(2)_l × U(1)_y, y que unificara por tanto la gravitación con el resto de las interacciones.

Edward Witten demostró en 1981 que el número total de dimensiones que se necesitarían sería al menos de once. Sin embargo, se pudo comprobar que la extensión de la teoría a once dimensiones no podía contener fermiones quirales, y por tanto sería incapaz de describir los campos de leptones y quarks.

Por otra parte, la supersimetría implica que por cada bosón existe un fermión con las mismas propiedades. La extensión supersimétrica de la Relatividad General es lo que se conoce como supergravedad (supersimetría local).

Joël Scherk (1946-1980) (a menudo citado como Joel Scherk) fue un francés teórico físico que estudió la teoría de cuerdas y supergravedad ^[1] . Junto con John H. Schwarz , pensaba que la teoría de cuerdas es una teoría de la gravedad cuántica en 1974. En 1978, junto con Eugène Cremmer y Julia Bernard , Scherk construyó el lagrangiano y la supersimetría transformaciones para supergravedad en once dimensiones ^[2] , que es uno de los fundamentos de la teoría-M .

Unos años antes, en 1978, Cremmer, Julia y Scherk habían encontrado que la supergravedad, precisamente en once dimensiones, tenía propiedades de unicidad que no se encontraban en otras dimensiones. A pesar de ello, la teoría no contenía fermiones quirales, como los que conocemos, cuando se compactaba en cuatro dimensiones. Estos problemas llevaron a gran parte de los teóricos al estudio de otro programa de unificación a través de dimensiones extra aún más ambicioso, la teoría de cuerdas.

No por haberme referido a ella en otros trabajos anteriores estará de más dar un breve repaso a las supercuerdas. Siempre surge algún matiz nuevo que enriquece lo que ya sabemos.

El origen de la teoría de supercuerdas data de 1968, cuando Gabriela Veneziano introdujo los modelos duales en un intento de describir las amplitudes de interacción hadrónicas, que en aquellos tiempos no parecía provenir de ninguna teoría cuántica de campos del tipo de la electrodinámica cuántica. Posteriormente, en 1979, Yaichiro Nambu, Leonard Susskind y Holger Nielsen demostraron de forma independiente que las amplitudes duales podían obtenerse como resultado de la dinámica de objetos unidimensionales cuánticos y relativistas dando comienzo la teoría de cuerdas.

En 1971, Pierre Ramona, André Neveu y otros desarrollaron una teoría de cuerdas con fermiones y bosones que resultó ser supersimétrica, inaugurando de esta forma la era de las supercuerdas.

Sin embargo, en 1973 David Gross, David Politzer y Frank Wilczek descubrieron que la Cromodinámica Cuántica, que es una teoría de campos gauge no abeliana basada en el grupo de color SU(3)_c, que describe las interacciones fuertes en términos de quarks y gluones, poseía la propiedad de la libertad asintótica. Esto significaba que a grandes energías los quarks eran esencialmente libres, mientras que a bajas energías se encontraban confinados dentro de los hadrones en una región con radio R de valor R ≈ hc/Λ ≈ 10^{-13 cm}.

Dicho descubrimiento, que fue recompensado con la concesión del Premio Nobel de Física a sus autores en 2.004, desvió el interés de la comunidad científica hacia la Cromodinámica Cuántica como teoría de las interacciones fuertes, relegando casi al olvido a la teoría de supercuerdas.

A pesar de todo, en 1974 Joel Scherk y John Schwarz hicieron la observación de que la teoría de cuerdas podía ser también una teoría cuántica de la gravitación. Sin embargo, este hecho pasó desapercibido durante casi una década. Además, las teorías de cuerdas tenían extrañas propiedades. Su versión más simple, la cuerda bosónica, sólo estaba definida en 26 dimensiones, y por si esto fuese poco, también presentaba un estado taquiónico, es decir, con masa al cuadrado negativa. Por otra parte, las supercuerdas parecían estar plagadas de anomalías (obstrucciones a la cuantización de la teoría que hacían altamente improbable que se los pudiera dar alguna explicación útil para la física fundamental.

Todo cambió, sin embargo, cuando en 1984 Michael Green y John Schwarz demostraron que las teorías de supercuerdas cerradas basadas en los grupos SO(32) y E₈ × E₈ estaban libres de anomalías si se definían en un espacio-tiempo de 10 dimensiones.

Ese mismo año, Gross, Harvey, Martinec y Rohm encontraron otro tipo de teorías de cuerdas consistentes denominadas heteróticas.

Como resultado de esos y otros muchos trabajos emergieron cinco teorías de cuerdas consistentes denominadas tipo I, tipo IIA, tipo IIB, heterótica SO(32) (HO) y heterótica E₈ × E₈ (HE). Todas consistentes exclusivamente en 10 dimensiones y estaban libres de taquiones.

       David Jonathan Gross

El de más edad de los cuatro, David Gross, hombre de temperamento imperativo, es temible en los seminarios cuando al final de la charla, en el tiempo de preguntas, con su inconfundible vozarrón dispara certeros e inquisidoras preguntas al ponente. Lo que resulta sorprendente es el hecho de que sus preguntas dan normalmente en el clavo.

La posibilidad de construir teorías realistas de las interacciones entre partículas fundamentales (incluyendo la gravitación) a partir de la teoría de supercuerdas surgió del trabajo seminal de Candelas, Strominger, Horowitz y Witten de 1985 donde se proponía el uso de la supercuerda heterótica E₈ × E₈ y la compactificación de las 6 dimensiones extra para dar lugar a espacios de Calabi-Yan (un tipo especial de propiedades o variedades compactas con tres dimensiones complejas). La idea era que mediante la elección apropiada de la variedad compactificada, el límite de la teoría a bajas energías sería similar al Modelo Estándar definido en las cuatro dimensiones ordinarias; es decir, la teoría cuántica de campos actualmente aceptada como la teoría correcta de las interacciones fuertes y electrodébiles basada en el grupo gauge SU(3)_C × SU(2)_L × U(1)_Y, que incluye la cromodinámica cuántica (grupo de color SU(3)_C) y la teoría de las interacciones electrodébiles basada en el grupo conocido como SU(2)_L × U(1)_Y, desarrollada en 1967 por Steven Weinberg, Abdus Salam y Sheldon Glashow y por la que se les concedió el Premio Nobel de Física en 1979.

De esta forma, durante los años ochenta se estudiaron con gran detalle numerosos espacios compactificados B de dimensión 6, tipo Calabi-Yan, junto con otros espacios, como por ejemplo, los llamados orbifoldios (variedades diferenciables cocientadas por grupos discretos) en un intento de tomas contacto con la fenomenología de bajar energías accesibles a los experimentos actuales. Además, las posibilidades podían aumentarse incluyendo campos gauge que podían estar definidos sobre B, dando lugar a diferentes líneas de flujo que se enrollarían y enlazarían de infinidad de formas dentro de B, sacando partido de su habitualmente intrincada topología.

En todo caso, el tamaño típico de espacio B era del orden de la longitud de Planck, L_p = 1’6 × 10^-33 cm*, que en unidades naturales es la inversa de la masa de Planck. Este hecho situaba fuera de las posibilidades reales el estudio experimental de sus propiedades. Además, a cada espacio B, ataviado de sus líneas de flujo, correspondería un posible vacío (estado fundamental o de menor energía) de la teoría. Sin embargo, en la medida que ésta sólo se podía determinar perturbativamente, es decir, en el régimen de interacción débil, no era posible seleccionar el verdadero vacío de la teoría a partir de primeros principios, sino tan sólo buscar aquellos que podían tener más posibilidades de establecer contacto con el mundo que observamos a nuestro alrededor.

emilio silvera

 Profesor sin plaza ni salario, salvo honorarios según las clases impartidas.

  del orden de 10^-8 Kg = 10¹¹ GeV; es la masa de una partícula cuya longitud de onda compton es igual a la longitud de Planck.

[?]