May
12
¿Qué es un Agujero Negro?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Agujeros negros ~
Clasificado en Agujeros negros ~
 Comments (9)
Comments (9)
Representar un Agujero negro no resulta nada fácil y, se hace de manera que aparezca en la imagen lo que se cree que podríamos ver en el caso de estar allí cerca, contemplando a uno de ellos, y, como existen varias formas teóricamente posibles de agujero negro, las representaciones que podemos contemplar pueden ser distintas las unas de las otras.

La NASA realizó la primera imagen animada digital de un agujero negro
Según sean estrellas medianas como nuestro Sol, grandes o muy grandes, lo que antes era una estrella, cuando finaliza el derrumbe o implosión, cuando la estrella es aplastada sobre sí misma bajo su propio peso, cuando finalice su ciclo y consuma todo el combustible nuclear que la hace brillar, tendremos una estrella enana blanca, una estrella de neutrones o un agujero negro.
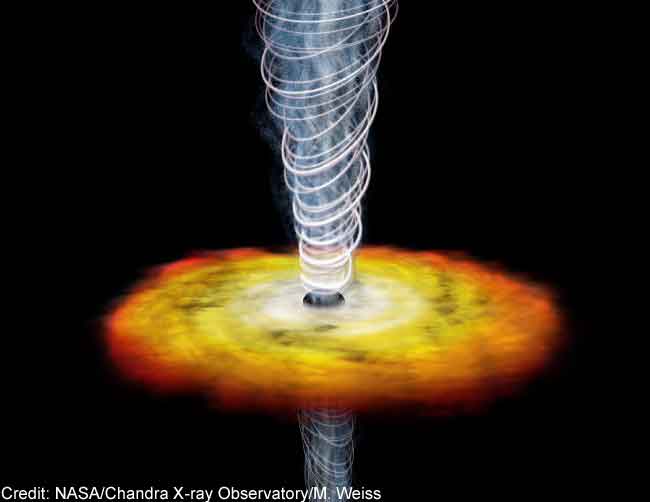
Alrededor del agujero negro puede formarse un disco de acreción cuando cae materia sobre él desde una estrella cercana que, para su mal, se atreve a traspasar el horizonte de sucesos. Es tan enorme la fuerza de gravedad que genera el agujero negro que, en tal circunstancias, literalmente hablando se come a esa estrella compañera próxima. En ese proceso, el agujero negro produce energía predominantemente en longitudes de onda de rayos X a medida que la materia está siendo engullida hacia la singularidad. De hecho, estos rayos X pueden ser detectados por satélites en órbita. Se ha localizado una enorme fuente de rayos X en el centro mismo de nuestra galaxia. En realidad han sido varias las fuentes localizadas allí, a unos 30.000 años luz de nosotros. Son serios candidatos a agujeros negros, siendo el más famoso Cygnus X-1.


Existen varias formas teóricamente posibles de agujeros negros. En el centro de la Galaxia existe uno
- Un agujero negro sin rotación ni carga eléctrica (Schwarzschild).
- Un agujero negro sin rotación con carga eléctrica (Reissner-Nordström).

En la práctica es más fácil que los agujeros negros estén rotando y que no tengan carga eléctrica, forma conocida como agujero negro de Kerr. Los agujeros negros no son totalmente negros; la teoría sugiere que pueden emitir energía en forma de radiación Hawking.

La estrella supermasiva, cuando se convierte en un agujero negro se contrae tanto que realmente desaparece de la vista, de ahí su nombre de “agujero negro”. Su enorme densidad genera una fuerza gravitatoria tan descomunal que la velocidad de escape supera a la de la luz, por tal motivo, ni la luz puede escapar de él.
En la singularidad, dejan de existir el tiempo y el espacio; podríamos decir que el agujero negro está fuera, apartado de nuestro universo, pero en realidad deja sentir sus efectos ya que, como antes dije, se pueden detectar las radiaciones de rayos X que emite cuando engulle materia de cualquier objeto estelar que se le aproxime más allá del punto límite que se conoce como horizonte de sucesos.
Con la explicación anterior he querido significar que, de acuerdo con la relatividad de Einstein, cabe la posibilidad de que una masa redujera sin límite su tamaño y se autoconfinara en un espacio infinitamente pequeño y que, alrededor de esta, se forme una frontera gravitacional a la que se ha dado el nombre de horizonte de sucesos. He dicho al principio de este apartado que en 1.916, fue Schwarzschild el que marca el límite de este horizonte de sucesos para cualquier cuerpo celeste, magnitud conocida como radio de Schwarzschild que se denota por:


Donde M es la masa del agujero negro, G es la constante gravitacional de Newton, y c2 es la velocidad de la luz elevada al cuadrado. Así, el radio de Schwarzschil para el Sol que tiene un diámetro de 1.392.530 Km, sería de sólo tres kilómetros, mientras que el de la Tierra es de 1 cm: si un cuerpo con la masa de la Tierra se comprimiera hasta el extremo de convertirse en una singularidad, la esfera formada por su horizonte de sucesos tendría el modesto tamaño de una bolita o canica de niños. Por otro lado, para una estrella de unas 10 masas solares el radio de Schwarzschild es de unos 30 kilómetros. Que para nuestro Sol, como he dicho antes, se quedaría en sólo tres kilómetros, tal es su grado de encogimiento sobre sí mismo.

Por otra parte, los acontecimientos que ocurren fuera del horizonte de sucesos en un agujero negro, tienen un comportamiento como cualquier otro objeto cósmico de acuerdo a la masa que presente. Por ejemplo, si nuestro Sol se transformara en un agujero negro, la Tierra seguiría con los mismos patrones orbitales que antes de dicha conversión del Sol en agujero negro.
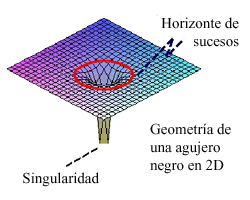
Ahora bien, y en función de la fórmula anteriormente descrita, el horizonte de sucesos se incrementa en la medida que crece la masa del agujero a medida que atrae masa hacia él y se la traga introduciéndola en la singularidad. Las evidencias observacionales nos invitan a pensar que en muchos centros de galaxias se han formado ya inmensos agujeros negros supermasivos que han acumulado tanta masa (absorciones de materia interestelar y estrellas) que su tamaño másico estaría bordeando el millón de masas solares, pero su radio de Schwarzschil no supera ni las 20 UA (unidad astronómica = 150 millones de Km), mucho menor que nuestro sistema solar.
Comprender lo que es una singularidad puede resultar muy difícil para una persona alejada de la ciencia en sí.
Es un asunto bastante complejo el de la singularidad en sí misma, y para los lectores más alejados de los quehaceres de la física, será casi imposible aceptarla. En el pasado, no fue fácil su aceptación, a pesar de las conclusiones radicales que expuso Kart Schwarzschild en su trabajo inspirado en la teoría y ecuaciones de Einstein. De hecho, hasta el mismo Einstein dudó de la existencia de tales monstruos cosmológicos. Incluso durante largo tiempo, la comunidad científica lo consideró como una curiosidad teórica. Tuvieron que transcurrir 50 años de conocimientos experimentales y observaciones astronómicas para empezar a creer, sin ningún atisbo de duda, que los agujeros negros existían realmente.
El concepto mismo de “singularidad” desagradaba a la mayoría de los físicos, pues la idea de una densidad infinita se alejaba de toda comprensión. La naturaleza humana está mejor condicionada a percibir situaciones que se caracterizan por su finitud, cosas que podemos medir y pesar, y que están alojadas dentro de unos límites concretos; serán más grande o más pequeñas pero, todo tiene un comienzo y un final pero… infinito, es difícil de digerir. Además, en la singularidad, según resulta de las ecuaciones, ni existe el tiempo ni existe el espacio. Parece que se tratara de otro universo dentro de nuestro universo toda la región afectada por la singularidad que, eso sí, afecta de manera real al entorno donde está situada y además, no es pacífica, ya que se nutre de cuerpos estelares circundantes que atrae y engulle.

En el Universo existen aún muchos misterios que debemos desvelar
La noción de singularidad empezó a adquirir un mayor crédito cuando Robert Oppenheimer, junto a Hartlan S. Snyder, en el año 1.939 escribieron un artículo anexo de otro anterior de Oppenheimer sobre las estrellas de neutrones. En este último artículo, describió de manera magistral la conclusión de que una estrella con masa suficiente podía colapsarse bajo la acción de su propia gravedad hasta alcanzar un punto adimensional; con la demostración de las ecuaciones descritas en dicho artículo, la demostración quedó servida de forma irrefutable que una estrella lo suficientemente grande, llegado su final al consumir todo su combustible de fusión nuclear, continuaría comprimiéndose bajo su propia gravedad, más allá de los estados de enana blanca o de estrella de neutrones, para convertirse en una singularidad.
Los cálculos realizados por Oppenheimer y Snyder para la cantidad de masa que debía tener una estrella para terminar sus días como una singularidad estaban en los límites másicos de M =~ masa solar, estimación que fue corregida posteriormente por otros físicos teóricos que llegaron a la conclusión de que sólo sería posible que una estrella se transformara en singularidad, la que al abandonar su fase de gigante roja retiene una masa residual como menos de 2 – 3 masas solares.
Oppenheimer y Snyder desarrollaron el primer ejemplo explícito de una solución a las ecuaciones de Einstein que describía de manera cierta a un agujero negro, al desarrollar el planteamiento de una nube de polvo colapsante. En su interior, existe una singularidad, pero no es visible desde el exterior, puesto que está rodeada de un horizonte de suceso que no deja que nadie se asome, la vea, y vuelva para contarlo. Lo que traspasa los límites del horizonte de sucesos, ha tomado el camino sin retorno. Su destino irreversible, la singularidad de la que pasará a formar parte.
Ni el mismo Einstein creyó la predicción que surgió de sus ecuaciones de la Relatividad General, no podía dar crédito a que, en el Universo pudieran existir tales “monstruos”.
Desde entonces, muchos han sido los físicos que se han especializado profundizando en las matemáticas relativas a los agujeros negros. John Malher (que los bautizó como agujeros negros), Roger Reyrose, Stephen Hawking, Kip S. Thorne (que recibió el Nobel por las Ondas gravitacionales), Kerr y muchos otros nombres que ahora no recuerdo, han contribuido de manera muy notable al conocimiento de los agujeros negros, las cuestiones que de ellas se derivan y otras consecuencias de densidad, energía, gravedad, ondas gravitacionales, etc, que son deducidas a partir de estos fenómenos del cosmos.
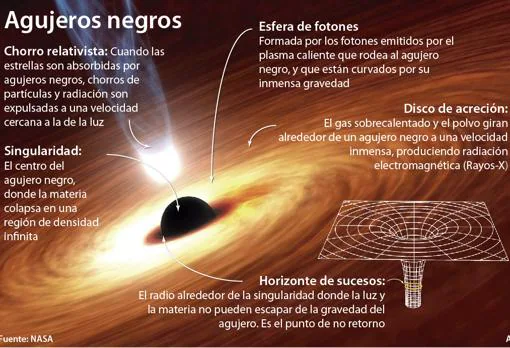
Se afirma que las singularidades se encuentran rodeadas por un horizonte de sucesos, pero para un observador, en esencia, no puede ver nunca la singularidad desde el exterior. Específicamente implica que hay alguna región incapaz de enviar señales al infinito exterior. La limitación de esta región es el horizonte de sucesos, tras ella se encuentra atrapado el pasado y el infinito nulo futuro. Lo anterior nos hace distinguir que en esta frontera se deberían reunir las características siguientes:
– debe ser una superficie nula donde es pareja, generada por geodésicas nulas;
– contiene una geodésica nula de futuro sin fin, que se origina a partir de cada punto en el que no es pareja, y que
– el área de secciones transversales espaciales jamás pueden disminuir a lo largo del tiempo.

Dicen que esta es la primera foto de un agujero negro
Todo esto ha sido demostrado matemáticamente por Israel, 1.967; Carter, 1.971; Robinson, 1.975; y Hawking, 1.978 con límite futuro asintótico de tal espaciotiempo como el espaciotiempo de Kerr, lo que resulta notable, pues la métrica de Kerr es una hermosa y exacta formulación para las ecuaciones de vacío de Einstein y, como un tema que se relaciona con la entropía en los agujeros negros.
No resulta arriesgado afirmar que existen variables en las formas de las singularidades que, según las formuladas por Oppenheimer y su colaborador Snyder, después las de kerr y más tarde otros, todas podrían existir como un mismo objeto que se presenta en distintas formas o maneras.
Ahora bien, para que un ente, un objeto o un observador pueda introducirse dentro de una singularidad como un agujero negro, en cualquiera que fuese su forma, tendría que traspasar el radio de Schwarzschild (las fronteras matemáticas del horizonte de sucesos), cuya velocidad de escape es igual a la de la luz, aunque esta tampoco puede salir de allí una vez atrapada dentro de los límites fronterizos determinados por el radio. Este radio de Schwarzschild puede ser calculado usándose la ecuación para la velocidad de escape:

Para el caso de fotones u objeto sin masa, tales como neutrinos (que tienen poca masa), se sustituye la velocidad de escape por la de la luz c2.
“En ausencia de resistencia de fricción, un objeto lanzado desde la Tierra puede escapar de ella, cuando su energía cinética iguala en magnitud a su energía potencial.”
La velocidad de escape está referida a la velocidad mínima requerida para escapar de un campo gravitacional. El objeto que escapa puede ser cualquier cosa, desde una molécula de gas a una nave espacial. Como antes he reflejado está dada por , donde G es la constante gravitacional, M es la masa del cuerpo y R es la distancia del objeto que escapa del centro del cuerpo del que pretende escapar (del núcleo). Un objeto que se mueva a velocidad menor a la de escape entra en una órbita elíptica; si se mueve a una velocidad exactamente igual a la de escape, sigue una órbita parabólica, y si el objeto supera la velocidad de escape, se mueve en una trayectoria hiperbólica.
Así hemos comprendido que, a mayor masa del cuerpo del que se pretende escapar, mayor será la velocidad que necesitamos para escapar de él. Veamos algunas:
|
Objeto |
Velocidad de escape |
| La Tierra | ………….11,18 Km/s |
| El Sol | ………….617,3 Km/s |
| Júpiter | ……………59,6 Km/s |
| Saturno | ……………35,6 Km/s |
| Venus | ………….10,36 Km/s |
| Agujero negro | ….+ de 299.000 Km/s |
Como se ve en el cuadro anterior, cada objeto celeste, en función de su masa, tiene su propia velocidad de escape para que cualquier cosa pueda salir de su órbita y escapar de él.
Para escapar de la atracción de un agujero negro se necesita ir más rápido que la luz, y, como sabemos, la velocidad de la luz, c, es el límite que marca el universo para poder desplazarse. así que,,, ¡Nada escapa de un agujero negro una vez traspasado el horizonte de sucesos·

La excepción está en el último ejemplo, la velocidad de escape necesaria para vencer la fuerza de atracción de un agujero negro que, siendo necesario superar la velocidad de la luz 299.792’458 Km/s, es algo que no está permitido, ya que todos sabemos que conforme determina la teoría de la relatividad especial de Einstein, la velocidad de la luz es la velocidad límite en nuestro universo; nada puede ir más rápido que la velocidad de la luz, entre otras razones porque el objeto sufriría la transformación de Lorentz y su masa sería infinita.
Podría continuar explicando otros aspectos que rodean a los agujeros negros, pero estimo que el objetivo que perseguía de hacer conocer lo que creemos que es un agujero negro y el origen del mismo, está sobradamente cumplido. De todas las maneras, no sería yo el que me presentara voluntario para visitar a uno de estos monstruos estelares de cuyas inmediaciones…hay que mantenerse alejados.
emilio silvera
















 Totales: 74.314.437
Totales: 74.314.437 Conectados: 38
Conectados: 38
























el 29 de marzo del 2017 a las 8:10
Después de leer todas estas explicaciones es difícil creer al científico del que nos comenta Kike que ha demostrado que, en el interior de los agujeros negros se forman multitud de estrellas. No parece nada fácil que en un lugar en el que la materia adopta su forma más densa se puedan dar las circunstancias para que se puedan formar estrellas.
Claro que cosas más raras hemos podido descubrir… ¡Ya veremos·
el 12 de mayo del 2020 a las 20:10
Haber, tenemos dos an de masas iguales en rumbo de colision, se supone que ambos sufren constracción de lorents según van acercándose, en teoría deberían formar un sistema binario por siempre, y no una fusión entre ambos.
Salvo que uno disponga de mayor potencial gravitatorio por nimio que fuera.
el 14 de mayo del 2020 a las 6:28
La lógica nos dice que, en principio, las cosas son tal como lo comentas, y, los agujeros negros binarios deben estar separados el uno del otro en varias decenas de parsecs. Sin embargo, también es lógico pensar que sus -orbitas finalmente se achiquen, ya que, poco a poco, van engullendo el material circundante (polvo y gas, estrellas…) y se incrementan sus masas de manera no uniforme, uno de ellos cogerá más materia que el otro y las masas se irán haciendo cada vez más desiguales, Finalmente, se irán acercando hasta que se produzca la fusión.
Se cree que estos procesos pueden durar millones de años. De todas las maneras, los modelos matemáticos que se han realizado para saber sobre el comportamiento de los agujeros negros binarios, hasta el momento no han despejado las muchas dudas que tenemos sobre lo que realmente puede pasar en un escenario similar y son muchas las conjeturas que sobre el tema existen.
Saludos.
el 15 de mayo del 2020 a las 19:20
Resulta que la velocidad de escape está en función de la masa del objeto del que tratamos de escapar de su gravedad, el sol 53 km/s, la tierra 11km/s, un agujero negra estelar 300.000km/s, un agujero supermasivo 300.000 km/s.
Algo no cuadra, en los agujeros negros la velocidad de escape no la determina la masa del an.y para el resto de objetos planetas, estrellas, pulsares, nuetronica, galaxias, cúmulos de galaxias, si. etc.
el 16 de mayo del 2020 a las 3:56
Hola muchachada.
La velocidad de escape es directamente proporcional a la masa de un objeto e inversamente proporcional a su radio (o distancia de su centro).
Por ejemplo: la velocidad de escape en la superficie de la Tierra es (aprox.) 11 km/s. Si la Tierra tuviera el mismo tamaño (radio) pero mayor masa (mayor densidad), esa velocidad sería mayor.
Si la masa de la Tierra se comprimiera hasta formar un hipotético agujero negro, su radio de Schwarzschild sería de 9 milímetros y su velocidad de escape en su superficie sería de… 300 000 km/s. Pero si medimos a 6400 km de distancia (radio medio actual) su velocidad de escape será de… 11 km/s !!!
Cuanto más lejos del centro se mide, menor es la velocidad de escape. En los agujeros negros ocurre lo mismo.
En su “superficie” determinada por el radio de Schwarzschild, todos tienen una velocidad de escape de 300.000k/s porque su masa es casi infinitamente densa. Dentro de ese límite ni la luz puede escapar. Pero a mayor distancia del centro, más allá de ese radio, la velocidad de escape disminuye en forma inversamente proporcional, siendo naturalmente la luz lo primero que escaparía.
En concreto, hay agujeros negros pequeños, grandes y supermasivos y en todos su velocidad de escape es de 300.000k/s pero siempre medida en su “superficie” (a mayor o menor distancia del centro) ; a medida que nos alejemos del centro su velocidad de escape decrecerá.
Saludos cordiales.
el 16 de mayo del 2020 a las 5:17
El problema de la velocidad de escape está muy bien estudiado y comprobado por la ciencia (sólo tenemos que preguntarle a los de la NASA), sabemos lo que nos cuesta hacer salir de la Tierra a todos esos ingenios que mandamos al Espacio para cumplir misiones de diferentes pelajes.
En relación al Agujero Negro, todos sabemos lo que pasa con la materia que les circunda, sea gas y polvo o una estrella que, atrevida ella, se pasa del límite en la cercanía del “monstruo” y es engullida poco a poco.
El amigo Nelson lo explica bien y, hasta donde podemos saber, las cosas son tal como las explica.
Saludos.
el 16 de mayo del 2020 a las 8:58
Muy buena explicación Nelson.
Bien, vamos a rizar el rizo, tenemos una galaxia, con un an central, vía láctea, su fuerza gravitacional es la suma de todas sus estrellas y demás y a esto añadiríamos la del propio an. 4000.000 millones de soles. En teoría no habría forma posible de escapar de la vía láctea, de ninguna manera, sin embargo más de un objeto es expulsada de la misma. 537km/s.
En función de la distancia al centro cambia la velocidad de escape. No obstante dicho supuesta nave tiene que sortear la masa total de dicha galaxia. ¿Que más da que este concentrada ma o menos? La masa de la galaxia siempre es la misma y no varía por que varíe el radio de la misma.
el 16 de mayo del 2020 a las 23:52
Hola muchachada.
Tratemos de no confundir.
Si se lee mi comentario anterior, no se puede decir que no importa el radio de una galaxia si la masa es la misma.
Si el radio disminuye (supongamos que se comprime la galaxia) su masa no varía pero la velocidad de escape será mayor. ¿Porqué? BIEN FÁCIL. Porque aumentó la densidad y por tanto su gravedad es mayor en la superficie.
El ejemplo de Pedro no sirve porque entre otras confusiones, confunde la masa total de la Vía Láctea con la masa del agujero negro de su centro. La velocidad de escape en su superficie (EN SU BORDE EXTERIOR) como bien dice es de 537 k/s porque su masa total (INCLUÍDO su A. N. central) es de 10 billones de masas solares y su radio unos 53 000 años luz.
Si se comprimiera tanto hasta transformarse en un A. N. supermasivo de 10 billones de masas solares, su velocidad de escape en su superficie sería de 300000 k/s
Ya está establecida una fórmula para calcular las velocidades de escape y se pueden calcular con dicha fórmula conociendo las dos variables. Si se va a insistir con esto buscaré la fórmula para terminar.
En el caso de la Vía Láctea, esas medidas son las que son y son las que determinan esa velocidad de escape en su superficie.
Su agujero negro central tiene una masa de (“grosso modo”) 4 millones de masas solares confinadas en una esfera de 22 millones de Km de radio. En su superficie, la velocidad de escape es de 300 000 k/s y a medida que “nos alejemos” la velocidad de escape será menor… hasta llegar a la “superficie” de la Vía Láctea en que; ya lo dijo Pedro, esa velocidad es de 537K/s. (Debemos ir sumando el resto de la masa de la Vía Láctea a medida que se va incluyendo dentro de un radio creciente).
¿Y porqué en la superficie de un agujero negro la velocidad de escape es siempre de 300000 km/s? Porque la relación entre su masa y su radio es constante siendo su densidad casi infinita. Un agujero negro pequeño tendrá poca masa y un radio pequeño. Un agujero grande tendrá un radio grande.
Como la velocidad de escape es inversamente proporcional a la distancia y directamente proporcional a la masa, siendo en ambos (y todos) los casos de densidad casi infinita, esa velocidad de escape relativista es prácticamente constante.
Saludos cordiales.
el 17 de mayo del 2020 a las 7:51