Oct
24
Más allá del Modelo Estándar ¿Qué habrá?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (6)
Comments (6)
“… el Modelo Estándar es, en la historia, la más sofisticada teoría matemática sobre la naturaleza. A pesar de la palabra “modelo” en su nombre, el Modelo Estándar es una teoría comprensiva que identifica las partículas básicas y especifica cómo interactúan. Todo lo que pasa en nuestro mundo (excepto los efectos de la gravedad) es resultado de las partículas del Modelo Estándar interactuando de acuerdo con sus reglas y ecuaciones.”


La Física actual busca una teoría más amplia que el modelo estándar . Una teoría que dé una descripción completa, unificada y consistente de la estructura fundamental del universo. ¿Será la compleja Teoría de cuerdas,que integra también la interacción gravitatoria?
El modelo estándar es una poderosa herramienta pero no cumple todas las expectativas; no es un modelo perfecto. En primer lugar, podríamos empezar por criticar que el modelo tiene casi veinte constantes que no se pueden calcular. Desde luego, se han sugerido numerosas ideas para explicar el origen de todos estos parámetros o números inexplicables y sus valores, pero el problema de todas estas teorías es que los argumentos que dan nunca han sido enteramente convincentes. ¿Por qué se iba a preocupar la naturaleza de una fórmula mágica si en ausencia de tal fórmula no hubiera contradicciones? Lo que realmente necesitamos es algún principio fundamental nuevo, tal como el principio de la relatividad, pero no queremos abandonar todos los demás principios que ya conocemos. Ésos, después de todo, han sido enormemente útiles en el descubrimiento del modelo estándar. El mejor lugar para buscar un nuevo principio es precisamente donde se encuentran los puntos débiles de la presente teoría y, construimos máquinas como el LHC para que nos diga lo que no sabemos.
Una regla universal en la física de partículas es que para partículas con energías cada vez mayores, los efectos de las colisiones están determinados por estructuras cada vez más pequeñas en el espacio y en el tiempo. El modelo estándar es una construcción matemática que predice sin ambigüedad cómo debe ser el mundo de las estructuras aún más pequeñas. Pero existen varias razones para sospechar que sus predicciones pueden, finalmente (cuando podamos emplear más energía en un nivel más alto), resultar equivocadas.
Vistas a través del microscopio, las constantes de la naturaleza parecen estar cuidadosamente ajustadas sin ninguna otra razón aparente que hacer que las partículas parezcan lo que son. Hay algo muy erróneo aquí. Desde un punto de vista matemático no hay nada que objetar, pero la credibilidad del modelo estándar se desploma cuando se mira a escalas de tiempo y longitud extremadamente pequeñas, o lo que es lo mismo, si calculamos lo que pasaría cuando las partículas colisionan con energías extremadamente altas. ¿Y por qué debería ser el modelo válido hasta aquí? Podrían existir muchas clases de partículas súper pesadas que no han nacido porque se necesitan energías aún inalcanzables. ¿Dónde está la partícula de Higgs? ¿Cómo se esconde de nosotros el gravitón?

En el Modelo la Gravedad no está por ninguna parte, el Gravitón no se junta con los otros Bosones
Parece que el Modelo estándar no admite la cuarta fuerza y tendremos que buscar más profundamente, en otras teorías que nos hablen y describan además de las partículas conocidas de otras nuevas que están por nacer y que no excluya la Gravedad. Ese es el Modelo que necesitamos para conocer mejor la Naturaleza.
Claro que las cosas no son tan sencilla y si deseamos evitar la necesidad de un delicado ajuste de las constantes de la naturaleza, creamos un nuevo problema: ¿Cómo podemos modificar el modelo estándar de tal manera que el ajuste fino no sea necesario? Está claro que las modificaciones son necesarias, lo que implica que muy probablemente haya un límite más allá del cual el modelo tal como está deja de ser válido. El modelo estándar no será nada más que una aproximación matemática que hemos sido capaces de crear, de forma que todos los fenómenos que hemos observado hasta el presente están reflejados en él, pero cada vez que se pone en marcha un aparato más poderoso, tenemos que estar dispuestos a admitir que puedan ser necesarias algunas modificaciones del modelo para incluir nuevos datos que antes ignorábamos.
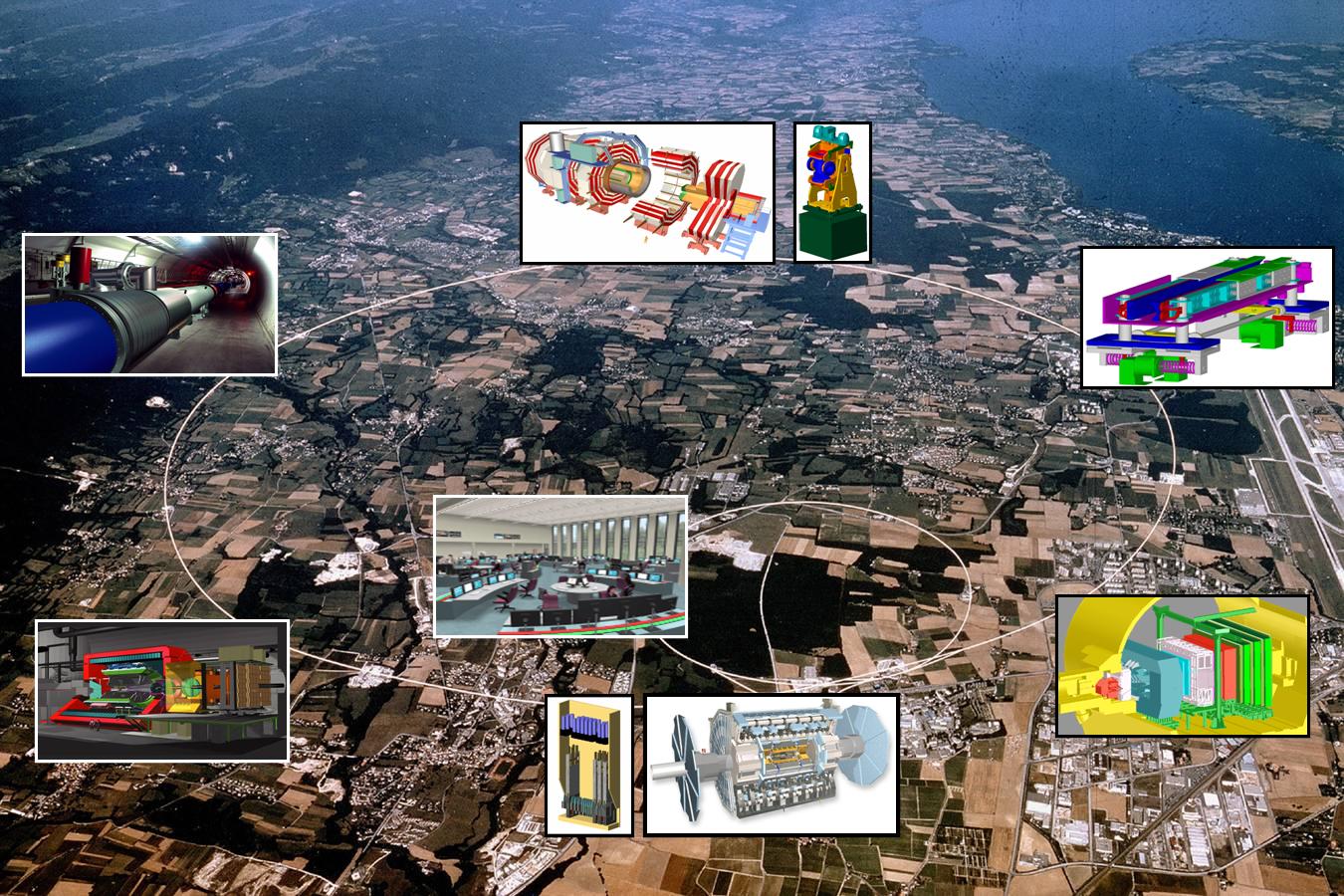
Más allá del modelo estándar habrá otras respuestas que nos lleven a poder hacer otras preguntas que en este momento, no sabemos ni plantear por falta de conocimientos. Si no conociéramos que los protones están formados por Quarks, ¿cómo nos podríamos preguntar si habrá algo más allá de los Quarks?
El gobierno de Estados Unidos, después de llevar gastados miles de millones de dólares, suspendió la construcción del super-colisionador superconductor de partículas asestando un duro golpe a la física de altas energías, y se esfumó la oportunidad para obtener nuevos datos de vital importancia para el avance de este modelo, que de momento es lo mejor que tenemos.
Se han estado inventando nuevas ideas, como la supersimetría y el technicolor. Los astrofísicos estarán interesados en tales ideas porque predicen una gran cantidad de nuevas partículas superpesadas, y también varios tipos de partículas que interaccionan ultradébilmente, los technipiones. Éstas podrían ser las WIMP’s (Weakly Interacting Massive Particles, o Partículas Masivas Débilmente Interactivas) que pueblan los huecos entre las galaxias, y serían así las responsables de la masa perdida que los astrofísicos siguen buscando y llaman “materia oscura”.

Que aparezcan “cosas” nuevas y además, imaginarlas antes, no es fácil. Recordemos cómo Paul Dirac se sintió muy incómodo cuando en 1931 dedujo, a partir de su ecuación del electrón, que debería existir una partícula con carga eléctrica opuesta. Esa partícula no había sido descubierta y le daba reparo perturbar la paz reinante en la comunidad científica con una idea tan revolucionaria, así que disfrazó un poco la noticia: “Quizá esta partícula cargada positivamente, tan extraña, sea simplemente el protón”, sugirió. Cuando poco después se identificó la auténtica antipartícula del electrón (el positrón) se sorprendió tanto que exclamó: “¡Mi ecuación es más inteligente que su inventor!”. Este último comentario es para poner un ejemplo de cómo los físicos trabajan y buscan caminos matemáticos mediante ecuaciones de las que, en cualquier momento (si están bien planteadas), surgen nuevas ideas y descubrimientos que ni se podían pensar. Así pasó también con las ecuaciones de Einstein de la relatividad general, donde Schwarzschild dedujo la existencia de los agujeros negros.
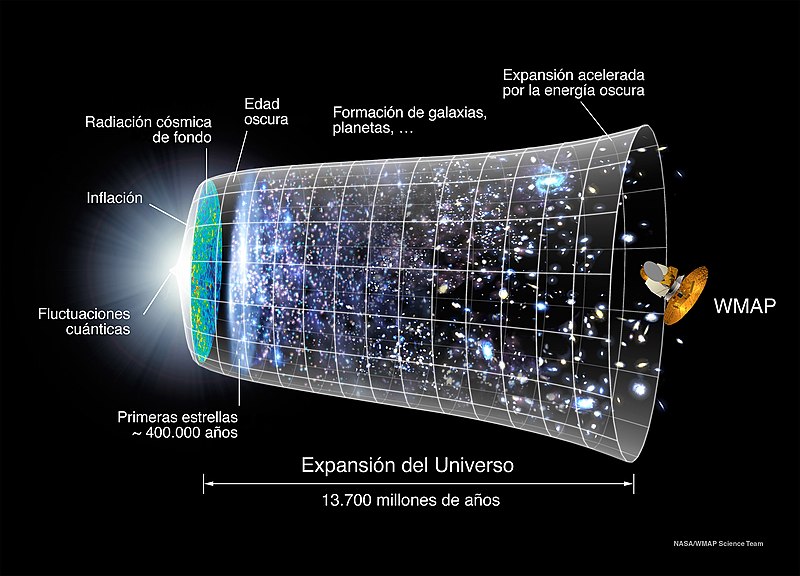
Se piensa que al principio del comienzo del tiempo, cuando surgió el Big Bang, las energías eran tan altas que allí reinaba la simetría total; sólo había una sola fuerza que todo lo englobaba. Más tarde, a medida que el universo se fue expandiendo y enfriando, surgieron las cuatro fuerzas que ahora conocemos y que todo lo rigen. Tenemos los medios, en los supercolisionadores de partículas, para viajar comenzando por 1.000 MeV, hasta finalizar en cerca de 1019 MeV, que corresponde a una escala de longitudes de aproximadamente 10–30 cm. Howard Georgi, Helen Quinn y Steven Weinberg descubrieron que ésta es la región donde las tres constantes de acoplamiento gauge se hacen iguales (U(1), SU(2) y SU(3)); resultan ser lo mismo. ¿Es una coincidencia que las tres se hagan iguales simultáneamente? ¿Es también una coincidencia que esto suceda precisamente en esa escala de longitud? Faltan sólo tres ceros más para alcanzar un punto de retorno. Howard Georgi y Sheldon Glashow descubrieron un modelo genuinamente unificado en el dominio de energías de 1019 MeV tal que, cuando se regresa de allí, espontáneamente surgen las tres fuerzas gauge tal como las conocemos. De hecho, ellos encontraron el modelo; la fórmula sería SU(5), que significa que el multiplote más pequeño debe tener cinco miembros.


“Materia y Energía Oscura”… Un Misterio…Sin resolver.
Y, a todo esto, ¿Dónde está esa energía oculta? ¿Y donde la materia? Podemos suponer que la primera materia que se creo en el Universo fue la que llamamos (algún nombre había que ponerle) “Materia Oscura”, esa clase de Ylem o sustancia primera del Universo que mejor sería llamarla invisible, ya que, de no ser así, difícil sería explicar cómo se pudieron formar las primeras estrellas y galaxias de nuestro Universo, ¿Dónde está el origen de la fuerza de Gravedad que lo hizo posible, sino en esa materia escondida?
¡Lo dicho! Necesitamos saber, y, deseo que de una vez por todas, se cumpla lo que dejó dicho Hilbert en su tumba de Gotinga (Alemania): “Tenemos que saber, ¡sabremos!. Pero…
¡Que sea pronto!
emilio silvera

















 Totales: 75.063.017
Totales: 75.063.017 Conectados: 1
Conectados: 1























el 24 de octubre del 2022 a las 7:49
Me hace una gracia que recursos se idean los físicos acerca de ciertas definiciones,osea definen tanto t y l de Planck como el producto de tres constante elevadas a unas unidades arbitrarias a,b,d
después durante la explicación surge otra constante llamada k, y de forma arbritaria decide así sin más ignorarla como tal, considera que ya es suficiente con las tres iniciales ,se me ocurre que de la misma manera podemos hacer lo mismo con los exponentes iniciales de a,b y d.
Como en todas disciplinas ocurre otro tanto en la física, no se distinguen en na de un conjunto de convencionalismos.
¿Hay alguna rama del saber que se sustraiga de tal tiranico exabrupto?
el 24 de octubre del 2022 a las 14:09
Amigo mío, creo que en todas las disciplinas científicas tienen sus cosillas.
el 24 de octubre del 2022 a las 18:53
Acerca de los distintos índices en la constante c., en su día ya plantee la misma cuestión:
Ya que estamos hablando de física y no matemáticas, se supone que en una ecuación todos sus componentes que la constituyen refrendan elementos físicos.
Me explico si hablan de c1 significa constante de la velocidad de la luz 3000.000km/s.
Si hablan de c elevado a otros índices ya no pueden estar hablando de fisica propiamente dicho salvo que utilicen otras unidades muy distintas a km/s. (Ya que nos han repetido hasta la saciedad que nada puede superar c en el vacío.)
Osea c5 y c3 en la definición de longitud y tiempo de planck sus unidades no pueden ser km/s, si quieren indicar un guaritmo muy elevado acerca de un componente físico que dejen muy claro sus unidades, pero en ningún caso podrán utilizar km/s , ya que no hay ningún componente físico que represente dicho guaritmo.
Conclusión:”¿Que mejor metáfora en ciencia que una ecuación bien definida? El cuño perfecto de toda una exaltacion”.
el 25 de octubre del 2022 a las 4:07
Hola muchachada.
El término c² no es un término aislado ni representa una velocidad. Es componente de una ecuación con términos de distinta naturaleza que expresa la equivalencia entre masa y su energía intrínseca. Está fehaciente, dramática y cruelmente demostrada en los bombardeos atómicos como el de Hiroshima, donde haciendo fisionar menos del 2% de unos pocos kilos de uranio a 600 mts de altura se provocó una explosión de 16 kilotones (equivalente a 16000 toneladas de TNT) que mató instantáneamente a casi 100.000 personas, otro tanto en las semanas sucesivas y en forma indirecta muchos miles más por enfermedades relacionadas con la radiación y quemaduras recibidas en las semanas, meses y años siguientes, además de la destrucción total de la ciudad, totalmente incinerada por una bola de fuego de centenares de metros de diámetro producida por una temperatura inicial de cerca de 1 000.000 de grados centígrados, similar a la del núcleo del Sol.
O también en el accidente de Chernobyl, donde 36 años después el reactor nº 4 se siga hundiendo, incandescente, mientras ya se llevan construídos dos “sarcófagos” de decenas de metros de espesor para aislar el núcleo del reactor que aún conserva el 95% de su material radiactivo original.
Yo creo que estas contundentes experiencias confirman la magnitud (y la veracidad) de una ecuación postulada teóricamente varias décadas antes y que hoy sensatamente nadie pondría en duda.
Saludos cordiales.
el 25 de octubre del 2022 a las 7:40
En el vídeo donde se explica definición de tiempo y longitud de Planck hace mención a c y sus unidades son longitud/segundo, y siempre que utilizan c nadie duda que sus unidades sean longitud/tiempo.
Yo no discrepo en cuanto al potencial destructivo que lleva implícito cualquier objeto cuya masa sea aquella que le queramos asignar.
Sino
E=mc2 Si las unidades de c son km/s cómo ecuación resulta un absoluto sin sentido.
A deferencia de E=mc2 si sus unidades son otras queriendo significar una componente muy elevada,representativo de un fenómeno u componente físico real, entonces si es tiene sentido.
Toda ecuación en física es un guiño de un fenómeno físico real a diferencia de una ecuación matemática que no se distingue en na de una abstracción lógica formal cuyo único recorrido encauzar un sentido.
el 25 de octubre del 2022 a las 17:19
Y para más inri acerca del carácter universal de dichas constantes, si las llaman constantes significa que son invariantes en cualquier contexto, u tiempo transcurrido bien, entonces ¿como historias se explica que podamos añadir un índice?
En resumidas en cualquier ecuación física si aparece una constante está si o si tiene que aparecer sin ningún índice decorativo por más que nosotros nos empeñemos en ello, en caso contrario un indicador de lo precario de aquello que tratamos de dilucidar.