Nov
30
TEORÍA DE LA PLANIFICACIÓN UNIVERSAL
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (1)
Comments (1)

La Geometría Esferoidal es el instrumento matemático utilizado por la Inteligencia Natural para la planificación de sus creaciones. Por ello, los movimientos sidéreos de los cuerpos sean componentes de sistemas planetarios solares o sistemas planetarios atómicos, son circulares y uniformes. Y las formas de los organismos naturales pueden traducirse en planificación geométrica combinando solamente trazos circulares del compás en movimiento uniforme sobre órbitas circulares.

El Universo escogió la geometría curva para los objetos como las estrellas y los mundos
“La Geometría es la esencia misma de Dios y del Mundo” –dijo Pitágoras— Platón afirmó que “únicamente los movimientos circulares y uniformes son dignos de la perfección de los cuerpos celestes; el cielo es geométrico porque es divino”. El movimiento de los cuerpos celestes—corroboró Copérnico—es uniforme, circular y perpetuo, o compuesto de movimientos circulares; el Universo es esférico”. Y Bailly nos enseñó que “hay que olvidar el movimiento que vemos para creer en el movimiento que no percibimos”.

Desarrollando la tesis consignada, y en forma coincidente con los pensamientos precedentemente transcriptos, todos los gráficos que ilustran el libro han sido ejecutados con el uso exclusivo del compás, moviéndose uniformemente por líneas circulares.

Pero debo formular esta importante aclaración: como ningún ser humano fue el autor de los planos de ninguna de las creaciones naturales existentes en el Universo o en nuestro mundo, ni tampoco fue el hombre el autor de los planos en base a los cuales se le dio su conformación al propio organismo humano o a cualquiera de sus partes, sino que todo ello ya había sido creado a una determinada (aunque ignorada) planificación antes de que el hombre mismo fuera creado y comenzara a pensar y razonar, lo único que podemos hacer los hombres es copiar (simplemente copiar) cualquier creación natural, tratando de captar geométricamente, con nuestro rudimentario lenguaje matemático, los planos que pudieron ser utilizados por la Inteligencia Natural al proyectar tales creaciones.
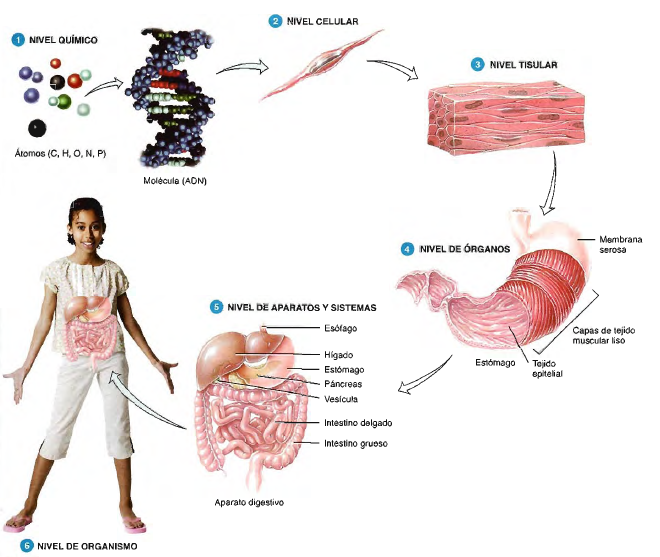
Las obras de la naturaleza no son humanas
En otras palabras: lo único que el hombre puede hacer, si desea comenzar a captar la técnica matemática con la cual la Inteligencia Natural ha planificado sus creaciones, es retrotraerse mentalmente al momento en que aquella Inteligencia decidió crear, por ejemplo, un sistema solar o un nuevo organismo natural o un átomo, y colocándose en la situación de ser el Creador, proyectar tal sistema sideral, empezando por el movimiento de sus mundos o de tal organismo o átomo utilizando una técnica que sólo puede ser geométrica.
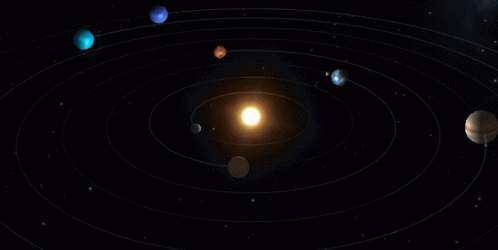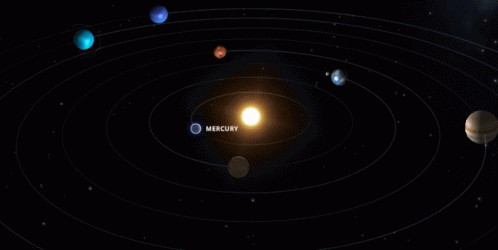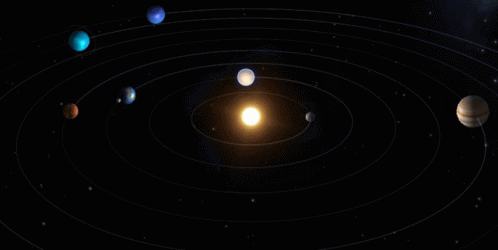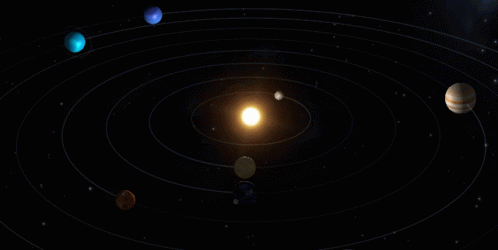
El hombre que tal cosa se proponga, debe decirse: “Si yo fuera la Inteligencia Natural y quisiera proyectar un sistema solar como el sistema solar en uno de cuyos planetas estamos viviendo, o tal organismo natural como nuestro cuerpo físico, lo planificaría de tal modo”. Y luego confrontar los resultados para verificar si el verdadero sistema solar con el que nosotros hemos planificado, o si nuestros planos (no dibujos, ni copias, ni fotografías, sino planos) de un organismo natural, lo revelan como tal, aunque sea como forma aproximada.

Así lo hice yo, Con el compás en la mano, como único instrumento, utilizando solo un trazo circular y moviéndolo únicamente por senderos circulares, busqué las orbitas de los planetas y el relieve de los organismos naturales combinando tales círculos con el resultado de que ilustran los gráficos de esta obra.
Esto significa, aunque es obvio decirlo, que todos los planos contenidos en el libro no son precisamente pretendidos planos de la Naturaleza descubiertos por mí, sino mis propios rudimentarios planos obtenidos en mi intento de planificar orbitas, organismos o átomos como si yo hubiera sido (Dios perdone tamaña pretensión) la Inteligencia Natural, lo que no impide a nadie, desde luego, que haga lo mismo, modificando la técnica y así sucesivamente hasta perfeccionarla de tal modo que un día el hombre de ciencia pueda lograr que su propia planificación de lo creado coincida con la real planificación universal.

La Naturaleza de Ovidio queda reflejada en sus pensamientos
Escrito transcripto por: su hermano Dante
TEORÍA DE LA PLANIFICACIÓN UNIVERSAL: OVIDIO PRACILIO
TESIS DEESTA OBRA
















 Totales: 75.589.992
Totales: 75.589.992 Conectados: 74
Conectados: 74























el 30 de noviembre del 2023 a las 19:59
El magnifico trabajo del gran pensador Don Ovidio, me ha traído a la memoria la importancia de la geometría curva.
Recuerdo aquí uno de esos extraños casos que surgió el día 10 de Junio de 1.854 con el nacimiento de una nueva geometría: la teoría de dimensiones más altas que fue introducida cuando Georg Friedrich Bernhard Riemann dio su célebre conferencia en la facultad de la Universidad de Göttingen en Alemania. Aquello fue como abrir de golpe todas las ventanas cerradas durante 2.000 años de una lóbrega habitación que, de pronto, se ve inundada por la luz cegadora de un Sol radiante. Riemann regaló al mundo las sorprendentes propiedades del espacio multidimensional.
Su ensayo, de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios. La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría de espacios curvos surgía de sus ruinas. La revolución de aquel hecho iba a tener grandes consecuencias para el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la literatura en toda Europa. Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría su geometría en su famosa Teoría de la Relatividad.
Ciento treinta años después de su conferencia, los físicos utilizarían la geometría deca-dimensional para intentar unir todas las leyes del universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.
Riemann nació en 1.826 en Hannover, Alemania, y, pocas dudas pueden caber sobre el hecho cierto de que su trabajo estará en la Historia junto al de Euclides, Arquímedes, Newton y Gauss.
El problema que captó el interés de Riemann fue el colapso que, según él pensaba, suponía la geometría euclidiana, que mantiene que el espacio es tridimensional y “plano” (en el espacio plano, la distancia más corta entre dos puntos es la línea recta; lo que descarta la posibilidad de que el espacio pueda estar curvado, como en una esfera).
Para Riemann, la geometría de Euclides era particularmente estéril cuando se la comparaba con la rica diversidad del mundo. En ninguna parte veía Riemann las figuras geométricas planas idealizadas por Euclides. Las montañas, las olas del mar, las nubes y los torbellinos no son círculos, triángulos o cuadrados perfectos, sino objetos curvos que se doblan y retuercen en una diversidad infinita.
Riemann, ante aquella realidad, se rebeló contra la aparente precisión matemática de la geometría griega, cuyos fundamentos, descubrió él, estaban basados en definitiva sobre las arenas movedizas del sentido común y la intuición, no sobre el terreno firme de la lógica y la realidad del mundo.
La ruptura decisiva con la geometría euclidiana llegó cuando Gauss pidió a su discípulo Riemann que preparara una presentación oral sobre los “fundamentos de la geometría”. Gauss estaba muy interesado en ver si su discípulo podía desarrollar una alternativa a la geometría de Euclides.
El alumno superó con mucho la prueba y regaló al mundo una nueva geometría que, más tarde, sirvió para conocer el Universo y los objetos que lo pueblan.
Riemann creó su tensor métrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresarse, a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a2 + b2 = c2.
El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional).
El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas.
Precisamente, el tensor de Riemann permitió a Einstein formular su teoría de la gravedad y posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de super-gravedad, supersimetría y, finalmente, las supercuerdas.
Para asombro de Einstein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854 que le había enviado su amigo Marcel Grossman, rápidamente se dio cuenta de que allí estaba la clave para resolver su problema. Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de la relatividad general. Esta fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E = mc2. La reinterpretación física de la famosa conferencia de Riemann se denomina ahora relatividad general, y las ecuaciones de campo de Einstein se sitúan entre las ideas más profundas de la historia de la ciencia.
Bueno, lo dejo aquí, creo que para un comentario me he pasado en las explicaciones pero, cuando aparece una idea tan brillante como la de Riemann… Uno puede entrar en el éxtasis de tan asombrosas ideas que pueden cambiar el curso de la Historia de la Humanidad.