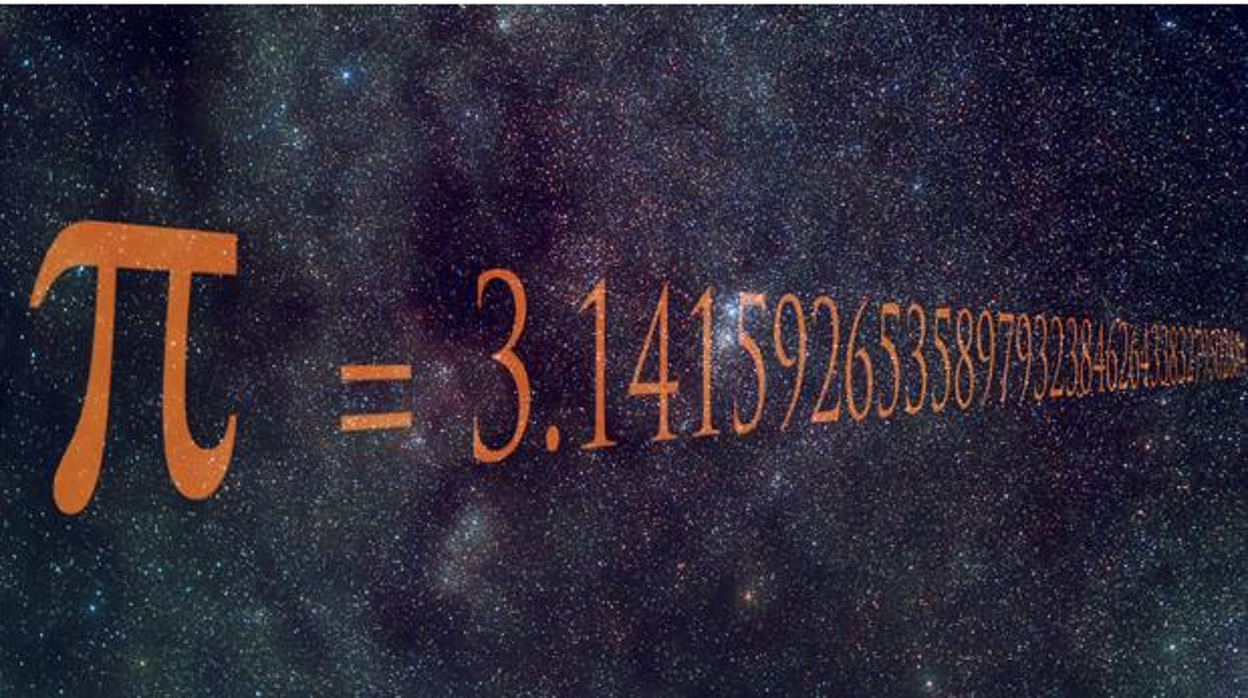May
23
Algún día habrá contacto
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
May
23
Nuestra percepción y la realidad: Dos cosas distintas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en La realidad cambiante ~
Clasificado en La realidad cambiante ~
 Comments (0)
Comments (0)
No todos vemos el mundo de la misma manera
Nuestra realidad es la que cada uno de nosotros percibimos, entendemos y actuamos de manera diferente en la vida. Cada uno poseemos nuestra propia realidad del mundo y de nosotros mismos. Estamos construidos a base de creencias, y esas creencias son las que influyen de manera decisiva en nuestra realidad y en nuestra conducta, por lo tanto, son las culpables de que consigamos o no nuestros objetivos. Básicamente nuestra realidad está formada por nuestras creencias.
La corteza cerebral es la porción externa del encéfalo, también llamada “materia gris”. Genera los pensamientos intelectuales más complejos y controla los movimientos corporales
“Nuestra tarea más urgente es dejar de identificarnos con el pensamiento, dejar de estar poseídos por él” Eso nos aconseja Eckhart Tolle, y, no siempre resulta ser de esa manera, Hay ocasiones en la que, nuestros pensamientos son la guía que nos pueden llevar al buen destino, y, si lo que dice (que no lo aclara) está referido a los pensamientos de los otros, simplemente se trata de discernir dónde radica la verdad, en lo que nos dicen o en lo que nosotros creemos. Claro que, no todos creen siempre en lo correcto.
Lo cierto es que, la única realidad vendrá de los descubrimientos que son desvelados y nos muestran los secretos d la Naturaleza.
Nosotros los humanos, nunca estamos seguros de nada y, buscando esa seguridad, creamos modelos con los que tratamos de acercarmos más y más a esa realidad que presentimos, y, para ello, encontramos las maneras de aproximarnos a esa realidad “presentida”.

Pero vayamos a algo concreto y pensemos, por ejemplo, en la técnica reiterativa que se utiliza para obtener “soluciones” en casos como el problema de los tres cuerpos (por ejemplo) tiene un inconveniente. A veces no funciona, no siempre podemos decir a priori si va a funcionar o no. La técnica que se aplica para “resolver” las ecuaciones diferenciales pertinentes (recordemos que no se pueden resolver analíticamente) implica realizar aproximaciones sucesivas, en las cuales, como es sabido, el primer paso del proceso de cálculo sólo da una solución aproximada; el segundo paso añade (con un poco de suerte) una correccción para obtener una aproximación más precisa de la realidad; el tercer paso nos da una aproximación aún mejor, y así sucesivamente hasta que nos parezca que la aproximación es lo suficientemente buena para el objetivo que nos hayamos propuesto. Pero nunca podremos conseguir con exactitud la “respuesta” que encaja a la perfección con el comportamiento de los objetos del mundo real en lo que se centra nuestro interés en ese determinado momento y sobre ese objetivo en particular.
Los primeros números datan del 7.000 a.C., durante la época egipcia. En tiempos de la primera dinastía, los egipcios contaban con la escritura jeroglífica, cuyos símbolos intentaban representar un número o una idea.
Ninguna idea nos ha llegado de manera instantánea y depurada en todos sus conceptos, sino que, han sido ideas que han tenido que ir siendo depuradas más y más a conseguir esa realidad que buscábamos haciendo que, el esquema encontrado, se parezca lo más posible al mundo que nos rodea y que podemos observar. Esa es, en pocas palabras la historia de la Relatividad de Einstein que a junto muchas ideas y conceptos para conseguir sus teorías que están muy cercas de lo que el mundo es.

Lo que hacemos es sumar una serie de números -en principio, una serie de números infinitamente larga- A los matemáticos les interesa estas series infinitas para sus propios objetivos, independientemente de la importancia que puedan tener para los estudios del comportamiento de las cosas tales como los planetas que orbitan alrededor del Sol, y conocen una gran cantidad de series infinitas cuyas sumas se comportan lo suficientemente bien como para ofrecer una aproximación cada vez mejor de un número concreto.
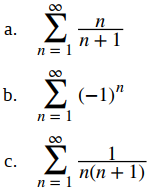
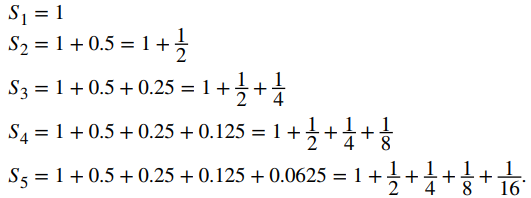
En esta aproximación muestra la prueba de texturizado del modelo 3D finalmente seleccionado.
Un buen ejemplo lo constituye uno de los procedimientos que se utilizan habitualmente para calcular el valor aproximado de π, el cociente entre la circunferencia de un círculo y su diámetro. Se puede calcular realmente el valor de π/4, con tanta precisión como se desee, sumando la serie numérica:
1 – 1/3 + 1/5 – 1/7 ….
Esto nos da una primera aproximación del valor de π que sería (4 x 1), que no es muy brillante; una segunda aproximación cuyo valor sería 2,6666… (4 x 2/3), que es algo mejor, y que, curiosamente, se encuentra al otro lado de la respuesta «correcta»; una tercera aproximación que sería 3,46666…, y así sucesivamente. Estas aproximaciones van siendo cada vez mejores y convergen en el verdadero valor de π, en este caso concreto desde ambos lados. Pero el proceso es tedioso -la suma del primer millón de términos de la serie nos da para pi (π) un valor de 3,1415937, que sólo es correcto en sus cinco primeras cinco cifras decimales, Ni obstante, se puede calcular π de este modo hasta el grado de precisión que se desee (hasta alguna cifra de los decimales), si tienes la paciencia necesaria.


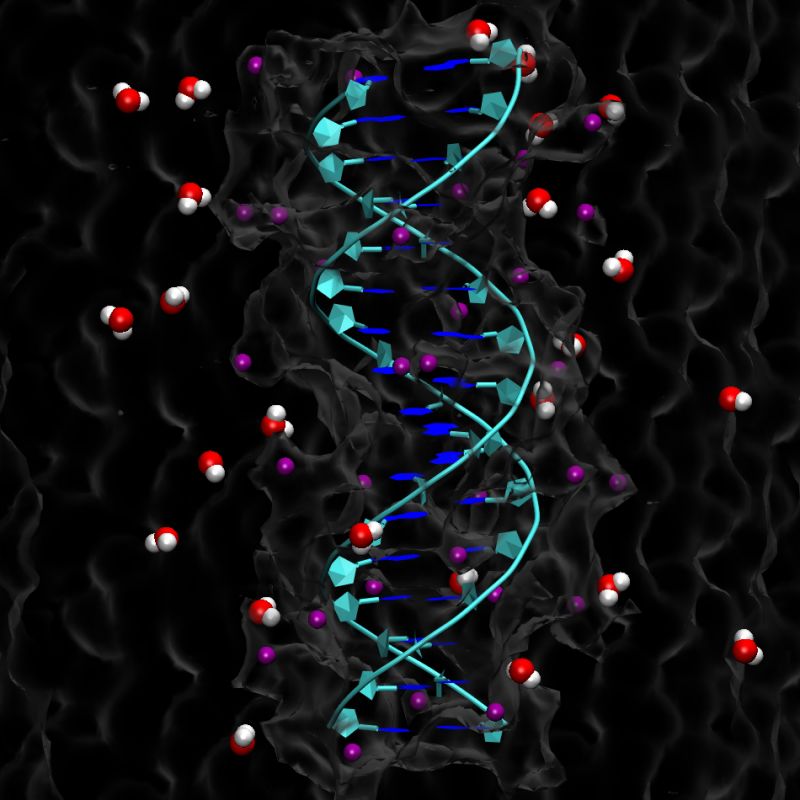

Hacemos una parada aquí para dejar una nota que nos dice que independiente de cualquier otra consideración, lo cierto es que, en matemáticas y la teoría del caos y entre otros temas. Si hablamos de Pi nos topamos con múltiples sorpresas y él está representado en el diseño de la doble espiral de ADN el Efecto mariposa y la Torah, entre otras muchísimas cosas que se escriben con Pi. Es un número misterioso que lo podemos ver por todas partes representado de una u otra manera. Desde la más remota antigüedad, fascinó a los más grandes pensadores.
No pocos están convencidos de la existencia de patrones que se repiten en los distintos órdenes de la vida. Descubrirlos implicaría, nada más y nada menos, que deducir el mundo. Yo no dejaría de lado, en todo esto la Teoría del Caos que podría definirse (¡en forma muy simplona!) como el estudio de sistemas complejos siempre cambiantes. Los resultados que consideramos ´impredecibles´ ocurrirán en sistemas que son sensibles a los cambios pequeños en sus condiciones iniciales. El ejemplo más común es conocido como “el efecto mariposa” “. La teoría supone que el batir de alas de una mariposa en la China durante un determinado período de tiempo podría causar cambios atmosféricos imperceptibles en el clima de New York.


Pi es la decimosexta letra del alfabeto griego y el símbolo que representa el misterio matemático más viejo del mundo: la proporción de la circunferencia de un círculo a su diámetro.
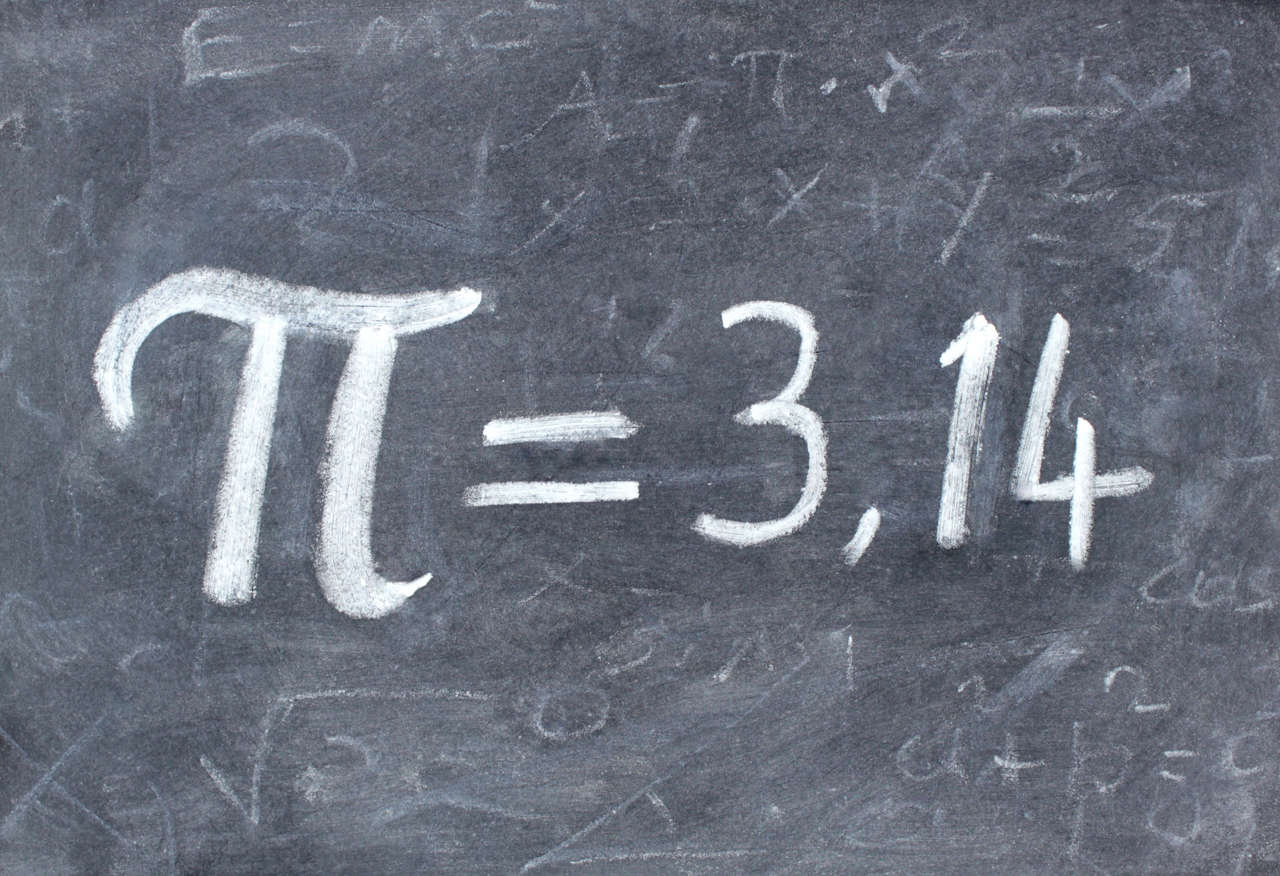
El registro escrito conocido más temprano de la proporción viene del año 1650 antes de Cristo en Egipto, donde un escriba calculó el valor como 3.16 (con un pequeñísimo error). Aunque ahora, nosotros tenemos métodos para calcular los dígitos de pi (3.1415…) sus restos de valor exacto todavía son un misterio.
Desde 1794, cuando se estableció que Pi era irracional e infinita, las personas han estado buscando un patrón en el cordón interminable de números.
Cosa curiosa, Pi puede encontrarse por todas partes, en la astronomía, en la física, en la luz, en el sonido, en el suelo, etc. Algunos cálculos advierten que tendría más de 51 mil millones de dígitos, pero hasta el momento no se ha detectado un patrón discernible que surja de sus números. De hecho, la primera sucesión 123456789 aparece recién cerca de los 500 millones de dígitos en la proporción.

En la actualidad hay algunas computadoras super-poderosas tratando de resolver la cuestión. En el film, la computadora bautizada por Max como Euclides literalmente “estalla” al acercarse a la verdad del cálculo. ¿Y entonces?… Azar, fe, creencias, ciencia, métodos…y siempre un misterio último sin resolver.
¿El hallazgo de patrones será la respuesta? Tal vez por eso los pitagóricos amaban la forma/patrón espiral… porque ella está por todas partes en la naturaleza: en los caracoles, en los cuernos del carnero, en las volutas de humo, en la leche sobre el café, en la cara de un girasol, en las huellas digitales, en el ADN y en la Vía Láctea.
3.1415926535897932384626433832795028841971693993…
Sí, son muchas las mentes más claras que se han interesado por este fascinante número π. En su libro de 1989 “La nueva mente del emperador”, Roger Penrose comentó sobre las limitaciones en el conocimiento humano con un sorprendente ejemplo: Él conjeturó que nunca más probable es saber si una cadena de 10 7s consecutivo aparece en la expansión digital del número pi . A tan sólo 8 años más tarde, Yasumasa Kanada utiliza una computadora para encontrar exactamente esa cadena, empezando por el dígito de pi …. 17387594880th.
Sin embargo, al final, algunos creen que, como todo esta relacionado, sabremos reconocer el mensaje que trata de enviarnos π y que, hasta el momento no hemos sabido comprender. Y, por otra parte, existen otras cuestiones que también estamos tratando de dilucidar para aproximarnos a esa realidad incomprendida que, estando aquí, no podemos ver. Por ejemplo:
Roger Penrose dedicó bastante más tinta en defender los argumentos de Shadows of Mind que en escribir dicha obra. En una de sus contrarréplicas, publicada en la revista Psyche (Enero, 1996), nos ofrece una de las versiones más claras de su famoso argumento.
Supongamos que todos los métodos de razonamiento matemático humanamente asequibles válidos para la demostración de cualquier tesis están contenidos en el conjunto F. Es más, en F no sólo introducimos lo que entenderíamos como lógica matemática (axiomas y reglas de inferencia) sino todo lo matemáticamente posible para tener un modelo matemático del cerebro que utiliza esa lógica (todos los algoritmos necesarios para simular un cerebro). F es, entonces, el modelo soñado por cualquier ingeniero de AI: un modelo del cerebro y su capacidad para realizar todo cálculo lógico imaginable para el hombre. Y, precisamente, ese es el modelo soñado porque la AI Fuerte piensa que eso es un ser humano inteligente. Así, cabe preguntarse: ¿Soy F? Y parece que todos contestaríamos, a priori, que sí.

¿Es la verdad inalcanzable?
Sin embargo, Roger Penrose, piensa que no, y para demostrarlo utiliza el celebérrimo teorema de Gödel, que venimos a recordar a muy grosso modo: un sistema axiomático es incompleto si contiene enunciados que el sistema no puede demostrar ni refutar (en lógica se llaman enunciados indecidibles). Según el teorema de incompletitud, todo sistema axiomático consistente y recursivo para la aritmética tiene enunciados indecidibles. Concretamente, si los axiomas del sistema son verdaderos, puede exhibirse un enunciado verdadero y no decidible (que se puede explicar) dentro del sistema.
Propiedad de los sistemas formales que disponen de un procedimiento de decisión efectivo, o un algoritmo, que permite determinar si toda expresión bien formada del sistema es o no es deducible dentro del sistema.
Si yo soy F, como soy un conjunto de algoritmos (basados en sistemas axiomáticos consistentes y recursivos), contendré algún teorema (proposiciones que se infieren de los axiomas de mi sistema) que es indecidible. Los seres humanos nos damos cuenta, somos conscientes de que ese teorema es indecidible. De repente nos encontraríamos con algo dentro de nosotros mismos con lo que no sabríamos qué hacer. Pero en esto hay una contradicción con ser F, porque F, al ser un conjunto de algoritmos, no sería capaz de demostrar la indecibilidad de ninguno de sus teoremas por lo dicho por Gödel… Una máquina nunca podría darse cuenta de que está ante un teorema indecidible. Ergo, si nosotros somos capaces de descubrir teoremas indecidibles es porque, algunas veces, actuamos mediante algo diferente a un algoritmo: no sólo somos lógica matemática.

Claro que, cómo podría un robot imitar nuestros múltiples, locos y dispares pensamientos:
- Los Computadores nunca podrán reemplazar la estupidez humana.
- El hombre nace ignorante, la educación lo idiotiza.
- Una persona inteligente resuelve problemas, el genio los evita.
- Las mujeres consideran que guardar un secreto, es no revelar la fuente.
- Todas las mujeres tienen algo bonito… así sea una prima lejana.
- La felicidad es una lata de atún, pero con el abrelatas un poco distante.
- El único animal que no resiste aplausos es el mosquito.
- El amor está en el cerebro, no en el corazón.
- Definición de nostalgia “es la alegría de estar triste”.
- “Mi segundo órgano favorito es el cerebro”.

Un Robot con su cerebro positrónico, nunca podrá solucionar un problema imprevisto como hacen nuestros cerenros, el cerebro artificial se limita a utilizar los datos que le han introducido, pero imaginar…
Vale, ¿y qué consecuencias tiene eso? Para la AI muy graves. Penrose piensa no sólo que no somos computadores sino que ni siquiera podemos tener un computador que pueda simular matemáticamente nuestros procesos mentales. Con esto Penrose no está diciendo que en múltiples ocasiones no utilicemos algoritmos (o no seamos algoritmos) cuando pensemos, sólo dice (lo cual es más que suficiente) que, habrá al menos algunas ocasiones, en las que no utilizamos algoritmos o, dicho de otro modo, hay algún componente en nuestra mente del cual no podemos hacer un modelo matemático, qué menos que replicarlo computacionalmente en un ordenador.

En ese pequeño objeto de poco más de 1,5 Kg., se encuentran asombrosas maravillas
Además el asunto se hace más curioso cuanto más te adentras en él. ¿Cuáles podrían ser esos elementos no computables de nuestra mente? La respuesta ha de ser un rotundo no tenemos ni idea, porque no hay forma alguna de crear un método matemático para saber qué elementos de un sistema serán los indecidibles. Esto lo explicaba muy bien Turing con el famoso problema de la parada: si tenemos un ordenador que está procesando un problema matemático y vemos que no se para, es decir, que tarda un tiempo en resolverlo, no hay manera de saber si llegará un momento en el que se parará o si seguirá eternamente funcionando (y tendremos que darle al reset para que termine). Si programamos una máquina para que vaya sacando decimales a pi, no hay forma de saber si pi tiene una cantidad de decimales tal que nuestra máquina tardará una semana, seis meses o millones de años en sacarlos todos o si los decimales de pi son infinitos. De esta misma forma, no podemos saber, por definición, qué elementos de nuestra mente son no computables. A pesar de ello, Penrose insiste en que lo no computable en nuestra mente es, nada más y nada menos, que la conciencia, ya que, explica él, mediante ella percibimos la indecibilidad de los teoremas. Es posible, ya que, aunque a priori no pudiéramos saber qué elementos no son decidibles, podríamos encontrarnos casualmente con alguno de ellos y podría ser que fuera la conciencia. Pero, ¿Cómo es posible que nuestro cerebro genere conciencia siendo el cerebro algo aparentemente sujeto a computación? Penrose tiene que irse al mundo cuántico, en el que casi todo lo extraño sucede, para encontrar fenómenos no modelizables por las matemáticas y, de paso, resolver el problema del origen físico de la conciencia.

Las neuronas no nos valen. Son demasiado grandes y pueden ser modelizadas por la mecánica clásica. Hace falta algo más pequeño, algo que, por su naturaleza, exprese la incomputabilidad de la conciencia. Penrose se fija en el citoesqueleto de las neuronas formado por unas estructuras llamadas microtúbulos. Este micronivel está empapado de fenómenos cuánticos no computables, siendo el funcionamiento a nivel neuronal, si acaso, una sombra amplificadora suya, un reflejo de la auténtica actividad generadora de conciencia. ¡Qué emocionante! Pero, ¿cómo generan estos microtúbulos empapados de efectos cuánticos la conciencia? Penrose dice que no lo sabe, que ya bastante ha dicho…

O sea señor Penrose, que después de todo el camino hecho, al final, estamos cómo al principio: no tenemos ni idea de qué es lo que genera la conciencia. Sólo hemos cambiado el problema de lugar. Si antes nos preguntábamos cómo cien mil millones de neuronas generaban conciencia, ahora nos preguntamos cómo los efectos cuánticos no computables generan conciencia. Penrose dice que habrá que esperar a que la mecánica cuántica se desarrolle más. Crick o Searle nos dicen que habrá que esperar a ver lo que nos dice la neurología… ¡Pero yo no puedo esperar!
Además, ¿no parece extraño que la conciencia tenga algo que ver con el citoesqueleto de las neuronas? La función del citoesqueleto celular suele ser sustentar la célula, hacerla estable en su locomoción… ¿qué tendrá que ver eso con ser consciente? Claro que en el estado actual de la ciencia igual podría decirse: ¿qué tendrá que ver la actividad eléctrica de cien mil millones de neuronas con que yo sienta que me duele una muela?
Todo eso está bien pero, ¿Qué es PI?

“Corta 1/9 del diámetro y construye un cuadrado sobre la longitud restante. Este cuadrado tiene el mismo área que el circulo”.

Una tablilla babilónica esconde la tabla trigonométrica más antigua del mundo

May
23
¿La teoría de cuerdas? ¿Dónde poder verificarla?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
E. Witten, uno de sus mejores divulgadores (Teoría M), dice que es una Teoría adelantada a su Tiempo
May
23
La búsqueda interminable
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Teoría de Supercuerdas ~
Clasificado en Teoría de Supercuerdas ~
 Comments (1)
Comments (1)
Investigadores del Instituto de Física de Altas Energías (IFAE, un consorcio de la Generalitat de Cataluña y la Universidad Autónoma de Barcelona) han finalizado un estudio con datos del experimento ATLAS que busca materia oscura en el Gran Colisionador de Hadrones (LHC). En concreto, han usado ‘monojets, un tipo de sucesos producidos en las colisiones de alta energía del acelerador del Laboratorio Europeo de Física de Partículas (CERN) para aclarar la producción de las llamadas WIMP, partículas propuesta para formar materia oscura.
Claro que no siempre se consiguen los deseos que se quedan en eso… ¡En ideas difíciles de plasmar en realidad!

Hay frases que están vacías y formamos oraciones que no podemos cumplir. Estos estudios indican que el 73 % de la masa del Universo está formado por la energía oscura, un 23 % es materia oscura (materia oscura fría y materia oscura caliente) y un 4 % materia bariónica.
Afirmaciones que son difíciles de confirmar, y, se deberían expresar diciendo: Parece que en el Universo existe…
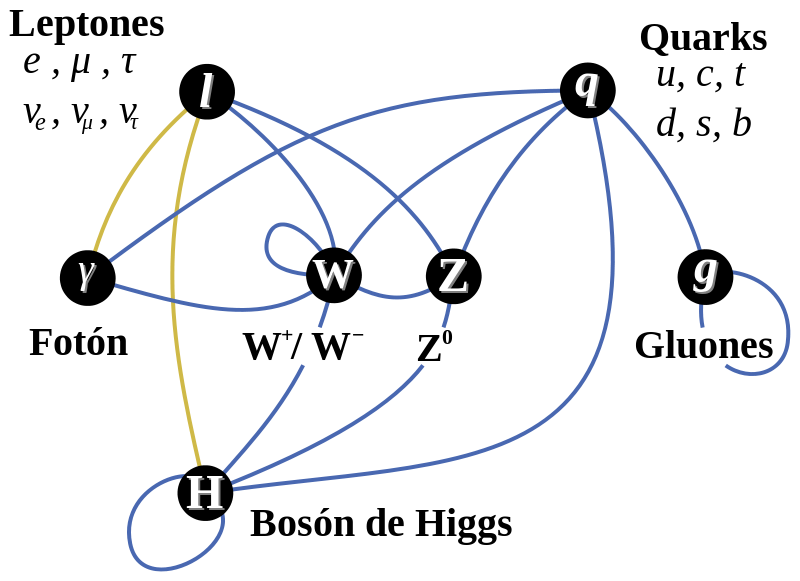
El Modelo Estandar es una máquina poderosa para el trabajo de los Físicos. Incluyen una veintena de parámetros metidos con calzador para las que “cuentas cuadren” (bueno 19 desde que apareció el Higgs). Sin embargo,

“La Teoría de Cuerdas es un intento por resolver uno de los grandes enigmas de la física teórica contemporánea y crear una teoría unificadora de sus distintos campos, es decir, una “teoría para el todo”.
Esta hipótesis científica y modelo fundacional sostiene que las partículas materiales que conocemos, como los elementos constitutivos del átomo son en realidad estados vibracionales de una «cuerda» o «filamento».
La Teoría de Cuerdas propone que el espacio-tiempo tiene muchas más dimensiones de las que podemos percibir (once, para ser exactos). Por eso, las “cuerdas” fundamentales pueden vibrar de muchos modos en todas estas dimensiones.”
Tenemos que ir más allá de los Quarks ¿Lo podremos lograr?
Los tiempos cambian, y, con los cambios llegan las nuevas doctrinas o creencias, o, ¿por qué no? nuevas teorías. Desde hace algún tiempo venimos dando vueltas y vueltas, en el campo de la Física, a esas avanzadas teorías que no podemos demostrar, toda vez que, al contrario del Modelo Estándar, no son (por ahora) verificables sus predicciones. Me estoy refiriendo, como habéis podido suponer a la Teoría de supercuerdas, La cuerda Heterotica, la Super-gravedad y Super-simetría, y, finalmente, la última versión que viene a ser un compendio de todas las demás, la Teoría M.

Como nos dice Brian Greene en uno de los capítulos del libro El tejido del Cosmos, que él titula: “Especulaciones sobre el espacio y el tiempo en la teoría M”, hoy, tres décadas después de la articulación de la teoría de cuerdas ,la mayoría de los que trabajan en ella, creen que aún no tenemos una respuesta general para la pregunta fundamental: ¿qué es la teoría de cuerdas? A pesar de que sabemos bastante de la teoría, sus características más elementales son familiares y, a estas alturas, casi cercanas. Tampoco debemos despreciar los éxitos que ha cosechado y, desde luego, es bien sabido todo lo que nos promete y también ¿cómo no? los desafíos que suponen lograr todas esas promesas que en ella están encerradas.
La relatividad especial tiene la constancia de la Velocidad de la luz, la relatividad general tiene el principio de Equivalencia, la mecánica cuántica tiene, el principio de Incertidumbre y, sin embargo, los teóricos de cuerdas aún siguen buscando algo de lo que carece la teoría de cuerdas que, precisamente es: el tipo de principio nuclear que se encontraron en aquellas otras teorías y le dan razón de ser y la sólida base que toda teo´ria necesita para ser.
Esa nueva teorías quiere explicarlo todo. Nada puede estar fuera de ella: El Universo que es, todo lo que existe, ahí estará
Un universo de Supercuerdas. El sueño de Einstein comienza a tomar realidad, a través de un nuevo paradigma de la ciencia que viene a romper con la toda la visión del mundo y del universo que teníamos hasta ahora, más allá de lo imaginable. Si la Teoría de cuerdas, finalmente resultase ser cierta, ese descubrimiento llevaría al mundo y a la conciencia humana hasta una nueva dimensión de su propia conciencia.
¿Cuáles es la ecuación más elegante y más bonita de la teoría de cuerdas? Claro que, verificar la Teoría está fuerza de nuestro alcance, se necesitaría una energía de 1019 GeV, lo que está muy lejos de nuestras posibilidades presentes.

Una de las primeras controversias sobre la teoría de supercuerdas que salta al tapete en las discusiones entre físicos teóricos es aquella en las que se subrayan diferencias como el caso del modelo estándar (que explica la interacción de fuerzas y partículas) y sobre el cual la física ha sido capaz de extraer predicciones contrastables en laboratorios, a diferencia en el marco de las supercuerdas que ello no ha sido posible, ya que no se han logrado hacer predicciones verificables con experimentos. Es decir, que todos los esfuerzos que se han gastado en su elaboración pueden acabar siendo un excelente ejercicio de especulación matemática. Claro que, de tener éxito, no sería esta la primera vez que un descubrimiento puramente teórico en la ciencia de la física acaba dando en el clavo y profundizando espectacularmente en el conocimiento de la naturaleza.
Según la Teoría de Supercuerdas, todo el universo manifestado, todo lo que percibimos como materia, desde las partículas subatómicas, hasta las galaxias, estaría soportado por una gran Matriz Subyacente, o Supercuerdas, que actuaría como una “gran sinfonía musical” detrás de todo lo que contemplamos como materia.
Ciertamente, si en realidad existen, están tan lejos de nosotros que, el viaje para “verlas” es demasiado costoso…, al menos de momento.
Hemos tratado, sin conseguirlo, de llegar hasta ellas, hasta las cuerdas vibrantes que residen en lo más profundo, más allá de los propios Quarks, y, hemos podido constatar que, nuestros ingenios y aceleradores, no son suficientes, no disponen la energía requerida para llegar hasta las cuerdas que serían la matriz del mundo. Allí, en su región de once dimensiones, todo es comprensión y armonía, todo cabe e incluso, la díscola Gravedad se junta apasiblemente con la Mecánica cuántica. Por eso algunos la llaman la Teoría del Todo, allí podemos encontrar todas las respuestas.
La supercuerda una poderosa estructura que no podemos localizar. Dicen que para poder hacerlo necesitamos de la energía de Planck, es decir, 1019 GeV, y, tal fuente de energía no existe aquí en nuestro mundo. Bueno, al menos no podemos disponer de ella, nuestras tecnologías no llegan a tener esa capacidad.

De la misma manera que no podemos sostener una galaxia en la mano, su inmensidad nos lo impide. Tampoco tenemos la capacidad de poder sujetar una “cuerda”, su infinitesimal tamaño, tampoco nos lo permite. Y, lo curioso del caso es que, de existir las cuerdas, esas enormes galaxias que podemos captar en el espacio interestelar, todas ellas, sin excepción, estarían hechas de cuerdas vibrantes que, al parecer, son los objetos que estarían más allá de los Quarks.
Los quarks son los ladrillos del Universo. Pero ¿están hechos de cosas más pequeñas? Contamos con muchas teorías, pero todavía no sabemos cuál es la más
es la más
Uno de los problemas ligados a la teoría de supercuerdas y que más resalta es el que tiene que ver con la propia pequeñez de las cuerdas. Mientras más pequeño es algo, más difícil es de ver. Y estas supercuerdas son tan super-pequeñas que no se observan esperanzas para hacer experimentos que nos puedan acercar a sus dimensiones. Sin experimentos no se pueden hacer comprobaciones de sus predicciones ni saber si son correctas o no. Exagerado, puede ser. Pero cada día se hace más insostenible su consideración sosteniéndola, tan sólo, con los fundamentos de un muy bien elaborado pensamiento experimental con el soporte de bellas ecuaciones matemáticas, o con algunas verificaciones experimentales que, para este caso, vienen a ser como indirectas, llámese Helio-3 y su super-fluidez, etc…

Branas, universos paralelos…¡cuerdas!
En esta teoría, hay problemas que se encuentran dentro de los enunciados de sus propios conceptos. Para desarrollar su formulación es necesario apelar a lo menos a diez dimensiones (en algunos casos, se han llegado hasta un número de veintiséis): espacio (3), tiempo (1) y a ellas se le agregan seis más como mínimo, que parecen estar enroscadas e invisibles para nosotros. Por qué aparecieron estas dimensiones adicionales a las cuatro que nos son familiares y por qué se atrofiaron en algún momento. Si en verdad existen, no lo sabemos. También, la teoría tiene decenas de miles de alternativas aparentemente posibles que no sabemos si son reales, si corresponden a miles de posibles universos distintos, o si sólo hay una realmente posible. En algunas de sus versiones se predice la existencia de 496 fuerzones, partículas como el fotón, que transmiten la fuerza entre 16 diferentes tipos de carga como la carga eléctrica. Afirmaciones como éstas, no comprobables por la imposibilidad de hacer experimentos, son las que plagan a la teoría de una multiplicidad de cuerdas. Ahora, las explicaciones más frecuentes que se dan para lo anterior, es de que los problemas surgen porque esta teoría se adelantó a su tiempo y no existe aún la estructura matemática consistente para formularla adecuadamente.
Incluso el salto cuántico es más fácil de verificar. Se estudia la manera que lo podamos hacer nosotros con nuestras naves del Futuro para burlar la velocidad de la luz
Las conclusiones a las que periódicamente llegan los adeptos a la TSC, se centran en el entusiasmo de proclamar que ésta otorga la única forma, hasta ahora, de poder contar en un futuro con una Teoría Cuántica consistente con la Gravedad. Como prácticamente todas las teorías de cuerdas, la TSC’s comienza con el concepto de dimensiones adicionales de Kaluza-Klein y comporta una enorme complejidad muy difícil de comprender para los que no están directamente involucrados en sus modelos. Con ella se aspira a resolver el más enigmático problema matemático que comporta la Física teórica en los finales del siglo veinte: la incompatibilidad matemática de los pilares fundamentales de la Mecánica Cuántica con la Teoría de la Relatividad General.

En cosmología, las partículas exóticas no sólo hay que proponerlas, es necesario también comprobar su existencia en experimentos de laboratorio y/o en observaciones.
La carencia de esa estructura matemática ha sido uno de los inconvenientes más serios que enfrentaba, y todavía lo es, la TSC y ello radica en las dificultades que presenta para hacer cálculos detallados. Sin embargo, en los últimos años, en alguna medida, especialmente después de la reunión de físicos teóricos cuerdistas realizada en la ciudad de Madrid, España, en el año 1995, ello se ha venido soslayando, ya que a través de el desarrollo de un conjunto de nuevas herramientas se ha logrado superar, en parte, las limitaciones matemáticas de la teoría.
Esas herramientas son las dualidades que vienen a ser como una especie, si se puede llamar así, de diccionario unificador que permite a los físicos «traducir» sus cálculos realizados en marcos teóricos asequibles a los modelos conocidos a marcos en que lo convencional no funciona. Es como si sabiendo calcular la electricidad y no el magnetismo; al descubrir que ambas fuerzas son dos caras de la misma moneda, se traducen las cantidades de una a otra, haciendo abordable el problema.

Sabemos de átomos y de Galaxias pero, ¿Qué es una cuerda? Una cuerda es un objeto con una dimensión espacial extendida, a diferencia de las partículas elementales que son de dimensión cero, como un punto. Al postular esta estructura unidimensional, muchas características de las teorías fundamentales de la física han emergido automáticamente.
No tenemos máquinas tan potentes como para verificar esa Teoría, ni el LHC ha podido
Hasta ahora, ninguna propuesta de la teoría de supercuerdas ha podido ser contrastada con experiencias experimentales y, mucho menos, observacionales. Sus logros sólo han podido ser chequeados en los correspondientes archivos computacionales y las pizarras de las oficinas de los matemáticos. Ellos han demostrado una serie de conjeturas matemáticas que surgen de manera natural de la TSC. Ahora, ello también a implicado que se haya venido generando una coincidencia o relación entre distintas estructuras matemáticas, de las que ni se sospechaba su existencia y han servido de motor e inspiración para algunos matemáticos.
La interpretación de los cálculos que se realizan describe un objeto tan diminuto, como las supercuerdas, que querer imaginarlas es como querer encontrar un grano de arroz perdido en algún lugar del Universo; es imposible. Su calculada pequeñez las hace inimaginable para la gran mayoría de los mortales humanos. Por hacernos una idea: la Tierra es 10-20 más pequeña que el universo y el núcleo atómico es 10-20 veces más pequeño que la Tierra. Pues bien, una supercuerda es 10-20 veces más pequeña que el núcleo atómico.
Es indudable que se trata de una teorización matemática que expuesta al común de la gente se hace casi «indigerible» o poco realista. A los especialistas en física teórica les pasa lo mismo. La física que hoy se maneja se hace cada vez más distante de la generalidad de los seres humanos, ya que no es tan sencilla como la de antaño; no sólo por que la descripción matemática de los fenómenos naturales se haya vuelto más complicada, sino porque resulta cada vez más difícil de imaginar. Esto se debe a que cada vez nos alejamos más y más de los objetos de nuestra experiencia cotidiana. Adentrándonos en el “universo” de la física cuántica, llegamos a ser conscientes de que, nuestro mundo, es una realidad propia de nuestras mentes, ya que, el “mundo real” la Naturaleza, es otra cosa bien distinta y, precisamente por eso, nos cuesta tanto comprender.

Ese “universo” de lo infinitamente pequeño, vibrante y luminoso, ¿Dónde estará?
Con la teoría de supercuerdas se ha llegado a un punto de abstracción que cuando nos zambullimos en su estudio y cálculos se llega a un momento en que la cabeza parece estallar, no por asombro, sino que por las incertidumbres que llega a concitar. Se parte con esperanzas y en el camino afloran –no voy a decir frustraciones– sino que una multiplicidad de inquietudes, ya que se va generando la sensación de que los resultados de los esfuerzos que se están realizando, nunca podrán ser comprobados.
Es cierto que en los procesos de hacer ciencia no se ha establecido como requisito que las teorías que se elaboran deban ser comprobadas en un pari-paso, de ello los científicos, por formación, están muy consciente. Pero la mera especulación intelectual, limitada para ser experimentada, en el tiempo tampoco es muy útil, ya que dejaría de ser considerada inserta dentro de los rangos de las exigencias consuetudinarias de lo que llamamos hacer ciencia.
Es aceptable considerar que aún la teoría de supercuerdas no ha alcanzado un desarrollo suficiente en el cual sus pronósticos puedan ser contrastados con experimentaciones en los actuales aceleradores de partículas. Pienso que aún se encuentra lejos de arrimarse a una maduración matemática que permita precisar cuales son sus predicciones. Los cálculos son bellos, pero sumamente difíciles.

Y, a todo esto, las ecuaciones de Einstein de la Relatividad General, subyacen en lo más profundo de la Teoría de Cuerdas, ya que, cuando se están desarrollando sus ecuaciones, allí aparecen, sin que nadie las llame, las ecuaciones de campo de la relatividad general que, es un subproducto de aquella otra teoría más avanzada. Tal secuencia, nos lleva a pensar que, la Teoría de supercuerdas es cierta, ya que, en caso contrario, ¿Por qué estaría allí Einstein?
También en la TSC, se encuentran involucradas las fuerzas fuertes de una manera tal que, antes de comenzar, comúnmente ya se encuentra limitadas las actuales capacidades humanas para calcular. Hay importantes pasos a realizar para poder aprender como llegar a inferir cálculos predictibles y poder ser testeados experimentalmente. Está claro que esta teoría se adelantó a su tiempo.
Es posible que para algunos sea inadmisible que se encuentre en el tapete de las discusiones de física teórica una teoría que todavía no precisa sus predicciones con un contraste experimental. Sin embargo, por las trayectorias que ya han experimentado las teorías de cuerdas, no reúnen aún los méritos como para ser consideradas científicas, o meros ejercicios de matemática abstracta. Por ahora, se puede señalar que parece ser que los físicos cuerdistas han ido más allá de los umbrales matemáticos aconsejables, con saltos de pasos que algún día deberán dar.

En el mundo de la física existen detractores de las supercuerdas de la talla y del genio como la de Richard Feymman, quien acerca del trabajo de los teóricos de las supercuerdas, afirmaba en una entrevista poco antes de morir, en 1988, «No me gusta que no calculen nada, no me gusta que no comprueben sus ideas, no me gusta que, para cada cosa que está en desacuerdo con un experimento, cocinen una explicación, un arreglo para decir bueno, todavía podría ser verdad.»
La teoría de supercuerdas es relativamente joven aún y durante su existencia ha mostrado una alta propensión a ser enfermiza. Surgen problemas, y se la deja de lado; se solucionan los problemas y una avalancha de trabajos resucitan la esperanza. En sus cerca de treinta años de vida, este vaivén ha ocurrido más de una vez.
Todo tiene su tiempo, y, Feynman, era ya un físico de bastante edad y de que ello a lo mejor era la causa de su resistencia a las ideas nuevas como algunos de sus maestros se resistían ante los profundos cambios conceptuales registrados en la física cuando él era joven. Las supercuerdas, dicen sus defensores, integrarían la física actual como la teoría de la relatividad de Einstein integró la gravitación de Newton explicando que sólo era un caso (el de nuestra escala del universo) de leyes más profundas y generales.
Nuevas geometrías, como en aquel tiempo en que llegó el llamado corte de Riemann, mediante el cual, se podñia acceder a dos regiones distantes del espacio, nos han traído estas nuevas teorías que cambian el concepto actual que, del Universo tenemos. El tensor métrico de Riemann permitió a Einstein formular su famosa teoría de la gravedad. Siempre ha sido así, las nuevas ideas nos trajeron las nuevas realidades de la Naturaleza y, si es así (que lo es), ¿por qué la teoría de cuerdas sería diferente?
Los matemáticos encuentran interesante esta teoría porque las dimensiones extra pueden tener geometrías muy complicadas y hay toda una rama matemática dedicada a explicar sus propiedades.
Los físicos-matemáticos piensan que, por ahora, es más lógico estudiar y observar el desarrollo de estas ideas teóricas cuerdistas como una consecuencia estética y grata en la consecución de una simple y definitiva teoría unificadora que reúna todos los requisitos necesarios para que pueda ser contrastada con pruebas experimentales.

LIGO
Hemos sido capaces de inventar aparatos para medir las ondas gravitatorias provenientes de los agujeros negros, y, como no podemos parar en el querer descubrir y saber lo que el Universo es, queremos seguir avanzando y tratamos de conseguir una teoría de la Gravedad Cuántica que, según todos los indicios va implícita en esta teoría de supercuerdas de más dimensiones.
No sé si se ha llegado a un límite en que la abstracción matemática sea un medio coadyuvante o una pesadilla para los físicos. Se quiere simplificar las cosas y, al final, se hacen más incomprensibles y complejas. Ya convertimos la gravedad, la fuerza electromagnética y las fuerzas nuclear fuerte y débil en campos. La gravedad, que no sabemos qué cosa es, pero que hace caer una piedra, ha pasado a ser algo mucho más abstracto que lo propuesto por Newton: un campo, una modificación de la estructura del espacio que nos rodea. Como nos movemos dentro de ese espacio, su estructura nos influye y nos hace actuar de cierta manera. Por eso caen la piedras, porque seguimos la forma del espacio, su geometría que viene dada por la materia que contiene.
Ya para el común de los humano ese, el más simple nivel de abstracción, les parece que se trata de algo que nunca podrán llegar a comprender. Pero ese sentimiento empeora cuando se pasa al siguiente nivel. Se trata de aquel que es considerado como los grandes almacenes de la física teórica, el objeto de estudio son los grupos de simetría mediante los cuales se relacionan esos campos y las partículas.
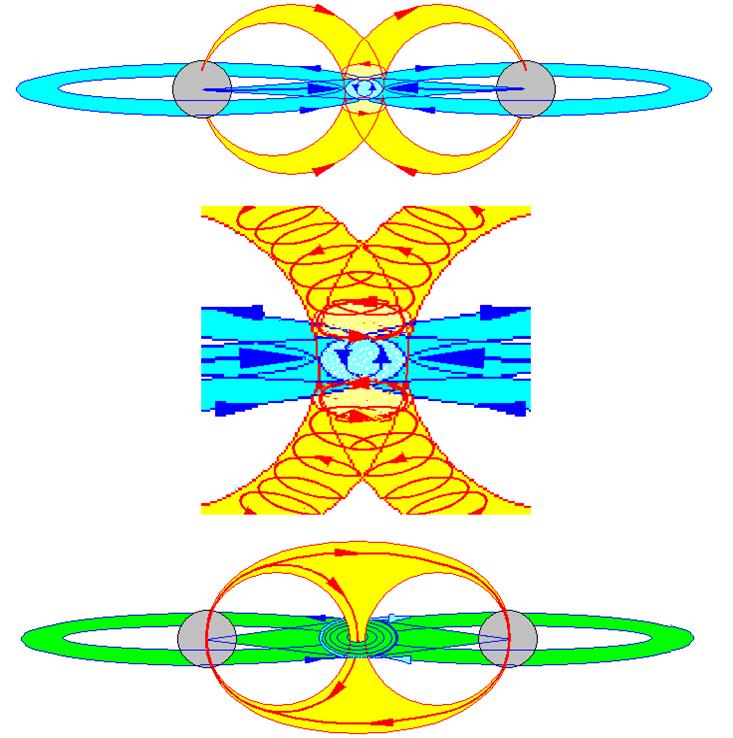
Grupos de simetría que relacionan campos y partículas donde las fuerzas están presentes.
El no va más del nivel de abstracción, se encuentra el mundo donde se cree que vive el constituyente fundamental de la materia: las supercuerdas. Estos objetos definen a través de su comportamiento esos estados que provocan la aparición de los grupo de simetría que a su vez relacionan la fuerza con la materia, y que al mismo tiempo explican la interacción de las partículas subatómicas y el comportamiento de los átomos.

Y, a todo esto, la Topología tiene mucho que decir en el mundo de la cuerda, toda vez que, en esta rama de las matemáticas pueden estar las respuestas a tan extraño objeto vibrante que nos dicen que podría ser lo más pequeño y al mismo tiempo lo más esencial que en el universo existe para su conformación
Al final, se trata de explicar todo y, a su vez, complicar todo. Por ello, decir que una supercuerda es un diminuto objeto vibrante que cohabita en un espacio con más dimensiones de simetría peculiar que el conocido tetradimensional es, prácticamente, no decir nada.
Hasta principios del año 2001, la premisa que se habían colocado los físicos de contar ya con una muy simple y gran teoría unificadora de las cuatro fuerzas, no se ha cumplido. Es posible que dentro del primer cuarto del siglo el intento culmine con un final feliz. Pero también es probable que no encontremos esa anhelada teoría, sino sólo una multiplicidad de teorías, cada vez más bellas y mejores.
Por ahora, lo cierto del caso es que, a pesar de algunas luces y pequeños éxitos, lo único firme y coherente es que el mundo se puede armar a partir de sesenta objetos puntuales cuyo origen desconocemos. Si se alcanzara algún día el objetivo de obtener todas las partículas y sus propiedades a partir de principios de simetría o de alguna cuerda única, por ejemplo, habríamos encontrado un nuevo nivel donde se concentra lo más elemental. Ya no serían los átomos, ni tampoco las partículas puntuales mismas, sino las simetrías o la cuerda. ¿Habríamos terminado? Es más que probable que no, pues nos preguntaríamos entonces de dónde salen esas simetrías o esa cuerda, y con alta probabilidad su estudio en detalle nos mostraría que en realidad hay más complejidad que la que aparecía a simple vista. La historia (¡la sabia historia!) muestra que este es un cuento sin final, y pareciera que cada vez que simplificamos las cosas, nuevos niveles de complejidad aparecen como fantasmas que están siempre acechándonos a la vuelta de cada esquina.

Parece que siempre estaremos entrando por una puerta misteriosa que nos lleva a un lugar oscuro en el que nunca sabemos lo que podemos encontrar. Es la Incertidumbre de la mecánica cuántica que, no se limita a estar allí, en ese mini-universo de lo pequeño. La Incertidumbre está presente en todo el Universo, y, nosotros, curiosos y deseosos de saber, no dudamos de adentrarnos en esos lugares desconocidos en busca de esas respuestas anheladas.
Así, podemos leer en cualquier diccionario que si preguntamos por la supercuerda, comienza diciéndonos: “La teoría de supercuerdas es un esquema teórico para explicar todas las partículas y fuerzas fundamentales de la naturaleza en una sola teoría, que modela las partículas y campos físicos como vibraciones de delgadas cuerdas super-simétricas, las cuales se mueven en un espacio-tiempo de más de 4 dimensiones.”
Y, a todo esto, de vez en cuando podemos encontrarnos con noticias llamativas como esta:

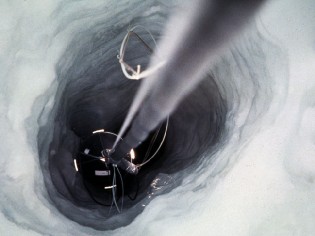
El funcionamiento de Amanda
“Científicos norteamericanos detectan la existencia de dimensiones adicionales. Las colisiones de neutrinos de alta energía con otras partículas corroboran uno de los postulados de la Teoría de Supercuerdas.
Científicos norteamericanos han detectado por primera vez indicios de la existencia de otras dimensiones más allá de las tres conocidas. Utilizando datos del telescopio Amanda, enterrado en el Polo Sur, han podido observar una decena de colisiones de neutrinos de alta energía con otras partículas elementales, obteniendo así la evidencia de las dimensiones adicionales sugerida por la Teoría de Supercuerdas. El descubrimiento no es concluyente y encontrará nuevas oportunidades cuando se inicie en 2009 el funcionamiento de otro telescopio 30 veces más potente, el Ice Cube, en el que participan diversas universidades europeas.”
¡Vivir para ver! Claro que, nosotros, que vivimos en un mundo de tres dimensiones espaciales y una temporal, lo único que podemos hacer es tener paciencia y esperar a que, esas lumbreras de la física, nos lleven de la mano hacia ese mundo mágico de las cuerdas que, según parece, nos mostrará un universo diferente, más completo y más real que el que ahora podemos observar.
Emilio Silvera V.
















 Totales: 72.271.660
Totales: 72.271.660 Conectados: 49
Conectados: 49