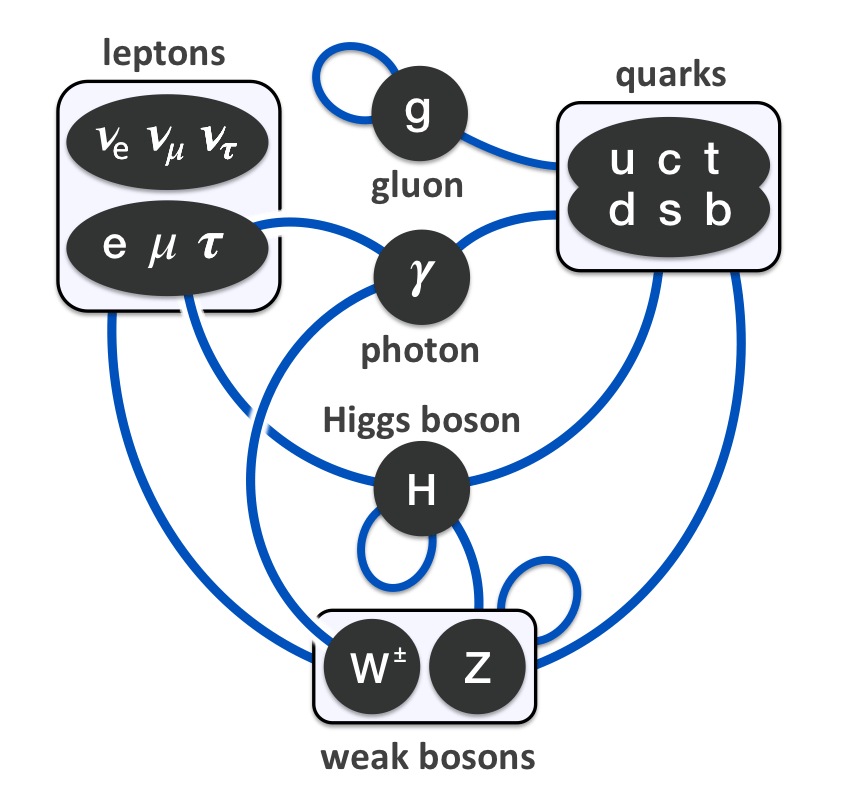
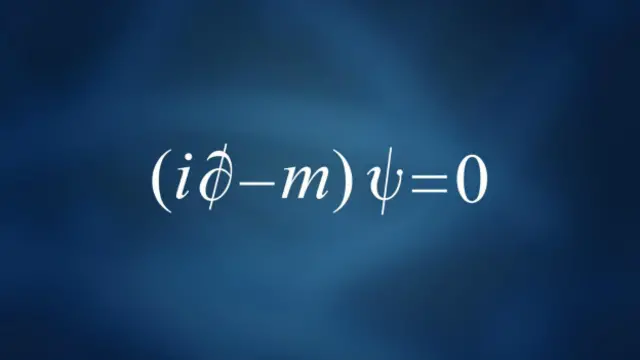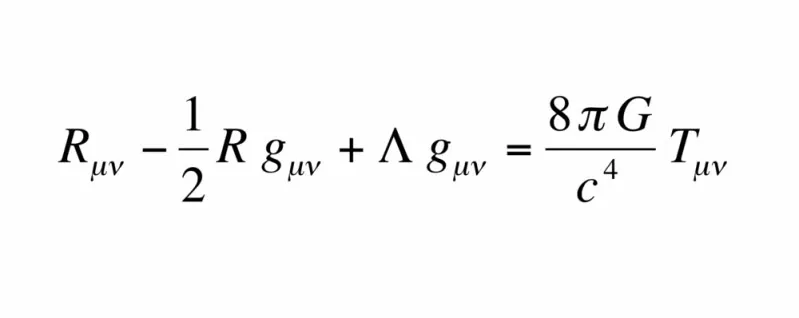Nov
5
¡La Hiperdimensionalidad! ¡Qué cosas nos cuentan!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)



El 21 de diciembre de 2010 científicos estadounidenses descubrieron “un vimana atrapado en un pozo del tiempo“ (un campo gravitatorio electromagnético, que sólo puede ocurrir en una dimensión invisible del espacio) en la ciudad de Balkh, Afganistán, lugar que alguna vez Marco Polo catalogó como: “Una de las ciudades más nobles y grandiosas del mundo”.
Los intentos por retirar el misterioso Vimana de la cueva donde había estado oculto durante por lo menos 5.000 años, causaron la “desaparición” de por lo menos 8 soldados norteamericanos, atrapados por el vórtex temporal ( nuestros cuerpos no pueden desplazarse como si nada del presente al futuro y del futuro al pasado sin cargarse el peso destructivo de las leyes de la fìsica, salvo si se logra bloquear el campo magnético, algo que aparentemente los científicos norteamericanos tardaron ocho cadáveres en descubrir y solucionar, probablemente con jaulas de Faraday ).
La existencia de este tipo de fenómenos no está demostrado por los científicos (caso contrario estaríamos hablando de leyes), pero los físicos teóricos coinciden en general que podrían ser posibles si se acepta la teoría del Multi-universo (un universo de por lo menos 11 dimensiones espaciotemporales) como estructura lógica y matemática. Atravesando esa especie de plasma líquido, nos podríamos trasladar a otros mundos, a otras galaxias.
Theodor Kaluza, ya en 1921 conjeturaba que si ampliáramos nuestra visión del universo a 5 dimensiones, entonces no habría más que un solo campo de fuerza: la gravedad, y lo que llamamos electromagnetismo sería tan sólo la parte del campo gravitatorio que opera en la quinta dimensión, una realidad espacial que jamás reconoceríamos si persistiéramos en nuestros conceptos de realidad lineal, similar a un holograma.
Bueno, independientemente de que todo esto pueda ser una realidad, lo cierto es que, nosotros, ahora en nuestro tiempo, hablamos de un universo con más dimensiones y, la carrera de las más altas dimensiones la inicio (como arrtiba se menciona) en el año 1919 (no el 1921) por Theodor Kaluza, un oscuro y desconocido matemático, cuando le presentó a Einstein mediante un escrito una teoría unificada que podía unificar, las dos grandes teorías del momento, la Relatividad General con el Magnetismo y podía realizarse si elaboraba sus ecuaciones en un espacio-tiempo de cinco dimensiones.
Teoría de la Relatividad de Kaluza
Así estaban las cosas cuando en 1.919 recibió Einstein un trabajo de Theodor Kaluza, un privatdozent en la Universidad de Königsberg, en el que extendía la Relatividad General a cinco dimensiones. Kaluza consideraba un espacio con cuatro dimensiones, más la correspondiente dimensión temporal y suponía que la métrica del espacio-tiempo se podía escribir como:
![]()

Theodor Kaluza
En 1921, Einstein presentó en la Academia Prusiana un artículo de Theodor Kaluza… en el que el campo gravitacional y electromagnético están unificados geométricamente en cinco dimensiones.
Así que, como hemos dicho, ese mismo año, Oskar Klein publicaba un trabajo sobre la relación entre la teoría cuántica y la relatividad en cinco dimensiones. Uno de los principales defectos del modelo de Kaluza era la interpretación física de la quinta dimensión. La condición cilíndrica impuesta ad hoc hacía que ningún campo dependiera de la dimensión extra, pero no se justificaba de manera alguna.
Klein propuso que los campos podrían depender de ella, pero que ésta tendría la topología de un círculo con un radio muy pequeño, lo cual garantizaría la cuantización de la carga eléctrica. Su diminuto tamaño, R5 ≈ 8×10-31 cm, cercano a la longitud de Planck, explicaría el hecho de que la dimensión extra no se observe en los experimentos ordinarios, y en particular, que la ley del inverso del cuadrado se cumpla para distancias r » R5. Pero además, la condición de periodicidad implica que existe una isometría de la métrica bajo traslaciones en la quinta dimensión, cuyo grupo U(1), coincide con el grupo de simetría gauge del electromagnetismo.

Einstein al principio se burló de aquella disparatada idea pero, más tarde, habiendo leido y pensado con más atenci`´on en lo que aquello podía significar, ayudó a Kaluza a publicar su idea de un mundo con cinco dimensiones (allí quedó abierta la puerta que más tarde, traspasarían los teóricos de las teorías de más altas dimensiones). Algunos años más tarde, , el físico sueco Oskar Klein publicó una versión cuántica del artículo de Kaluza. La Teoría Kaluza-Klein que resultó parecía interesante, pero, en realidad, nadie sabía que hacer con ella hasta que, en los años setenta; cuando pareció beneficioso trabajar en la supersimetría, la sacaron del baúl de los recuerdos, la desempolvaron y la tomaron como modelo.
Pronto, Kaluza y Klein estuvieron en los labios de todo el mundo (con Murray Gell-Mann, en su papel de centinela lingüistico, regañando a sus colegas que no lo sabían pronunciar “Ka-wu-sah-Klein”.

Pero, ¿Existen en nuestro Universo dimensiones ocultas?
Aunque la teoría de cuerdas en particular y la supersimetría en general apelaban a mayores dimensiones, las cuerdas tenían un modo de seleccionar su dimensionalidad requerida. Pronto se hizo evidente que la Teoría de cuerdas sólo sería eficaz, en dos, diez y veintiséis dimensiones, y sólo invocaba dos posibles grupos de simetría: SO(32) o E8 x E8. Cuando una teoría apunta hacia algo tan tajante, los científicos prestan atención, y a finales de los años ochenta había decenas de ellos que trabajaban en las cuerdas. Por aquel entonces, quedaba mucho trabajo duro por hacer, pero las perspectivas era brillantes. “Es posible que las décadas futuras -escribieron Schwarz y sus colaboradores en supercuerdas Green y Edward Witten- sea un excepcional período de aventura intelectual.” Desde luego, la aventura comenzó y, ¡qué aventura!
La Constante de Estructura Fina (α)
Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck). Si se duplica el valor de todas las masas no se puede llegar a saber, porque todos los números puros definidos por las razones de cualquier par de masas son invariables.
Puesto que el radio de compactificación es tan pequeño, el valor típico de las masas será muy elevado, cercano a la masa de Planck Mp = k-12 = 1’2 × 1019 GeV*, y por tanto, a las energías accesibles hoy día (y previsiblemente, tampoco en un futuro cercano – qué más quisieran E. Witten y los perseguidores de las supercuerdas -), únicamente el modo cero n = 0 será relevante. Esto plantea un serio problema para la teoría, pues no contendría partículas ligeras cargadas como las que conocemos.
¿Y si llevamos a Kaluza-Klein a dimensiones superiores para unificar todas las interacciones?
En este proceso llamado desintegración beta y debido a la interacción débil, un neutrón se transforma en un protón, un electrón y un (anti)neutrino electrónico cuando uno de los quarks del neutrón emite una partícula W–. Aquí queda claro que el término “interacción” es más general que “fuerza”; esta interacción que hace cambiar la identidad de las partículas no podría llamarse fuerza (todo representado en uno de los famosos diagramas de Feynman).

La descripción de las interacciones débiles y fuertes a través de teorías gauge no abelianas mostró las limitaciones de los modelos en cincodimensiones, pues éstas requerirían grupos de simetría mayores que el del electromagnetismo. En 1964 Bryce de UIT presentó el primer modelo de tipo Kaluza-Klein–Yang-Mills en el que el espacio extra contenía más de una dimensión.
El siguiente paso sería construir un modelo cuyo grupo de isometría contuviese el del Modelo Estándar SU(3)c × SU(2)l × U(1)y, y que unificara por tanto la gravitación con el resto de las interacciones.
Edward Witten demostró en 1981 que el número total de dimensiones que se necesitarían sería al menos de once. Sin embargo, se pudo comprobar que la extensión de la teoría a once dimensiones no podía contener fermiones quirales, y por tanto sería incapaz de describir los campos de leptones y quarks.
Por otra parte, la supersimetría implica que por cada bosón existe un fermión con las mismas propiedades. La extensión supersimétrica de la Relatividad General es lo que se conoce como supergravedad (supersimetría local).

Joël Scherk (1946-1980) (a menudo citado como Joel Scherk) fue un francés teórico físico que estudió la teoría de cuerdas ysupergravedad [1] . Junto con John H. Schwarz , pensaba que la teoría de cuerdas es una teoría de la gravedad cuántica en 1974. En 1978, junto con Eugène Cremmer y Julia Bernard , Scherk construyó el lagrangiano y supersimetría transformaciones parasupergravedad en once dimensiones, que es uno de los fundamentos de la teoría-M .

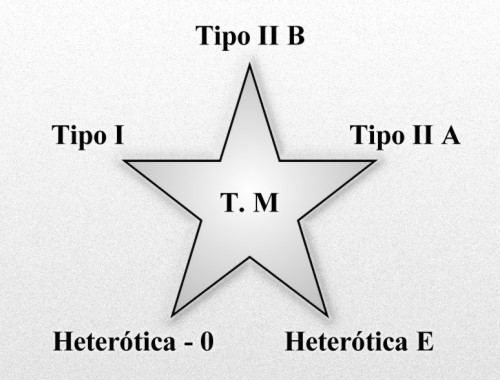
Unos años antes, en 1978, Cremmer, Julia y Scherk habían encontrado que la super-gravedad, precisamente en once dimensiones, tenía propiedades de unicidad que no se encontraban en otras dimensiones. A pesar de ello, la teoría no contenía fermiones quirales, como los que conocemos, cuando se compactaba en cuatro dimensiones. Estos problemas llevaron a gran parte de los teóricos al estudio de otro programa de unificación a través de dimensiones extra aún más ambicioso, la teoría de cuerdas.
No por haberme referido a ella en otros trabajos anteriores estará de más dar un breve repaso a las supercuerdas. Siempre surge algún matiz nuevo que enriquece lo que ya sabemos.
El origen de la teoría de supercuerdas data de 1968, cuando Gabriela Veneziano introdujo los modelos duales en un intento de describir las amplitudes de interacción hadrónicas, que en aquellos tiempos no parecía provenir de ninguna teoría cuántica de campos del tipo de la electrodinámica cuántica. Posteriormente, en 1979, Yaichiro Nambu, Leonard Susskind y Holger Nielsen demostraron de forma independiente que las amplitudes duales podían obtenerse como resultado de la dinámica de objetos unidimensionales cuánticos y relativistas dando comienzo la teoría de cuerdas.
En 1971, Pierre Ramona, André Neveu y otros desarrollaron una teoría de cuerdas con fermiones y bosones que resultó ser supersimétrica, inaugurando de esta forma la era de las supercuerdas.

David Jonathan Gross
Sin embargo, en 1973 David Gross, David Politzer y Frank Wilczek descubrieron que la Cromodinámica Cuántica, que es una teoría de campos gauge no abeliana basada en el grupo de color SU(3)c, que describe las interacciones fuertes en términos de quarks y gluones, poseía la propiedad de la libertad asintótica. Esto significaba que a grandes energías los quarks eran esencialmente libres, mientras que a bajas energías se encontraban confinados dentro de los hadrones en una región con radio R de valor R ≈ hc/Λ ≈ 10-13 cm.
Dicho descubrimiento, que fue recompensado con la concesión del Premio Nobel de Física a sus autores en 2.004, desvió el interés de la comunidad científica hacia la Cromodinámica Cuántica como teoría de las interacciones fuertes, relegando casi al olvido a la teoría de supercuerdas.
Se habla de cuerdas abiertas, cerradas o de lazos, de p branas donde p denota su dimensionalidad (así, 1 brana podría ser una cuerda y 2.Brana una membrana) o D-Branas (si son cuerdas abiertas) Y, se habla de objetos mayores y diversos que van incorporados en esa teoría de cuerdas de diversas familias o modelos que quieren sondear en las profundidades del Universo físico para saber, como es.
En la década de los noventa se creó una versión de mucho éxito de la teoría de cuerdas. Sus autores, los físicos de Princeton David Gross, Emil Martinec, Jeffrey Harvey y Ryan Rohn, a quienes se dio en llamar el cuarteto de cuerdas de Princeton.
El de más edad de los cuatro, David Gross, hombre de temperamento imperativo, es temible en los seminarios cuando al final de la charla, en el tiempo de preguntas, con su inconfundible vozarrón dispara certeros e inquisidoras preguntas al ponente. Lo que resulta sorprendente es el hecho de que sus preguntas dan normalmente en el clavo.
Gross y sus colegas propusieron lo que se denomina la cuerda heterótica. Hoy día, de todas las variedades de teorías tipo Kaluza-Klein que se propusieron en el pasado, es precisamente la cuerda heterótica la que tiene mayor potencial para unificar todas las leyes de la naturaleza en una teoría. Gross cree que la teoría de cuerdas resuelve el problema de construir la propia materia a partir de la geometría de la que emergen las partículas de materia y también la gravedad en presencia de las otras fuerzas de la naturaleza.

¿Por qué será que, cuando los físicos manejan las ecuaciones de la teoría de cuerdas, sin que nadie las llame, allí aparecen las ecuaciones de campo de la Relatividad General? ¿No será que que en esa teoría no verificada subyace una teoría de la Gr4avedad cuántica?
El caso curioso es que, la Relatividad de Einstein, subyace en la Teoría de cuerdas, y, si eliminamos de esta a aquella y su geometría de la Gravedad…todo resulta inútil. El gran Einstein está presente en muchos lugares y quizás, más de los que nos podamos imaginar.
Es curioso constatar que si abandonamos la teoría de la gravedad de Einstein como una vibración de la cuerda, entonces la teoría se vuelve inconsistente e inútil. Esta, de hecho, es la razón por la que Witten se sintió atraído inicialmente hacia la teoría de cuerdas. En 1.982 leyó un artículo de revisión de John Schwarz y quedó sorprendido al darse cuenta de que la gravedad emerge de la teoría de supercuerdas a partir solamente de los requisitos de auto consistencia. Recuerda que fue “la mayor excitación intelectual de mi vida”.
Gross se siente satisfecho pensando que Einstein, si viviera, disfrutaría con la teoría de supercuerdas que sólo es válida si incluye su propia teoría de la relatividad general, y amaría el hecho de que la belleza y la simplicidad de esa teoría proceden en última instancia de un principio geométrico, cuya naturaleza exacta es aún desconocida.atividad general de Einstein. Nos ayuda a estudiar las partes más grandes del Universo, como las estrellas y las galaxias. Pero los elementodiminutoso los átomos y las partículas subatómicas se rigen por unas leyes diferentes denominadas mecánica cuántica.
:format(jpg)/f.elconfidencial.com%2Foriginal%2F68c%2Fe14%2Fc51%2F68ce14c519946fca88d27a853ea6ce98.jpg)
Claro que, como todos sabemos, Einstein se pasó los últimos treinta años de su vida tratando de buscar esa teoría unificada que nunca pudo encontrar. No era consciente de que, en su tiempo, ni las matemáticas necesarias existían aún. En la historia de la física del siglo XX muchos son los huesos descoloridos de teorías que antes se consideraban cercanas a esa respuesta final que incansables buscamos.
Hasta el gran Wolfgang Pauli había colaborado con Heisenberg en la búsqueda de una teoría unificada durante algún tiempo, pero se alarmó al oir en una emisión radiofónica como Heisenberg decía: “Está a punto de ser terminada una Teoría unificada de Pauli-Heisenserg, en la que sólo nos queda por elaborar unos pocos detalles técnicos.”
Wolfgang Pauli
Enfadado por lo que consideraba una hipérbole de Heisenberg que se extralimitó con aquellas declaraciones en las que lo inviolucraba sin su consentimiento, Pauli envió a Gamow y otros colegas una simple hija de papel en blanco en la que había dibujado una caja vacía. Al pie del dibujo puso estas palabras: “Esto es para demostrar al mundo que yo puedo pintar con Tiziano. Sólo faltan algunos detalles técnicos.”
Los críticos del concepto de supercuerdas señalaron que las afirmaciones sobre sus posibilidades se basaban casi enteramente en su belleza interna. La teoría aún no había repetido siquiera los logros del Modelo Estándar, ni había hecho una sola predicción que pudiera someterse a prueba mediante el experimento. La Supersimetría ordenaba que el Universo debería estar repleto de familias de partículas nuevas, entre ellas los selectrones (equivalente al electrón supersimétrico) o el fotino (equivalente al fotón).
Lo cierto es que, nada de lo predicho ha podido ser comprobado “todavía” pero, sin embargo, la belleza que conlleva la teoría de cuerdas es tal que nos induce a creer en ella y, sólo podemos pensar que no tenemos los medios necesarios para comprobar sus predicciones, con razón nos dice E. Witten que se trata de una teoría fuera de nuestro tiempo, las supercuerdas pertenecen al futuro y aparecieron antes por Azar.
Y, a todo esto, ¿Dónde están esas otras dimensiones?

Bueno, una cosa es segura…. ¡Siempre hay más de lo que podemos ver! Ni subido en lo más alto podemos ver todo lo que hay.
Emilio Silvera Vázquez
Oct
31
Acercarse a la velocidad de la luz… trae consecuencias
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (33)
Comments (33)
Todos sabemos de los fenómenos que se pueden producir en algunos aspectos de la relatividad especial de Einstein. Él no quiso llamarla de esa manera y, había pensado que “teoría de la invariabilidad” que reflejaba el carácter invariable de la velocidad de la luz, entre otras cosas, estaría bien. Sin embargo, finalmente se quedó como la Teoría de la Relatividad Especial. La obra de Eintein demostraba que conceptos tales como espacio y tiempo, que anteriormente parecían estar sepados y ser absolutos, en realidad están entrelazados y son relativos. Einstein demostró además que otras propiedades físicas del universo, sorprendentemente, también están interrelacionadas. La más famosa de sus fórmulas constituye uno de los ejemplos más importantes.

“En otras palabras, la masa en sí misma es una medida de una cantidad equivalente de energía. Dicho de otra manera, un cambio (recordemos que los cambio se expresan con la letra griega delta mayúscula, Δ) en la cantidad de energía, E, de un objeto es directamente proporcional a un cambio en su masa, m.”
En esta escueta fórmula Einstein afirma que la energía (E) de un objeto y su masa (m) son conceptos independientes; podemos determinar la energía a partir de la masa del objeto (multiplicando esta dos veces por la velocidad de la luz, o sea por c2) o podemos determinar la masa conociendo su energía (dividiendo esta última dos veces por la velocidad de la luz). En otras palabras, la energía y la masa son las caras de una misma moneda. Claro que, el tipo de cambio es grande (c2 es una cantidad considerable). Una masa pequeña llega a producir una cantidad considerable de energía.

Equivalencia entre masa y materia
La energía que se comunica a un cuerpo libre puede integrarse en él de dos maneras distintas:
- En forma de velocidad, con lo cual aumenta la rapidez del movimiento.
- En forma de masa, con lo cual se hace “más pesado”.
La división entre estas dos formas de ganancia de energía, tal como la medimos nosotros, depende en primer lugar de la velocidad del cuerpo (medida, una vez más, por nosotros).

Captamos imágenes de galaxias situadas a 12 millones de años luz, y, desde luego, la podemos ver como eran entonces, hace 12 millones de año que es el Tiempo que tardó la luz de la galaxia en llegar a nosotros

¿Porqué la masa de un objeto aumenta a medida que incrementa su velocidad y de dónde sale esa masa que se suma.?
Como la velocidad de la luz es un límite que impone el Universo para moverse, resulta que un objeto que viaja y se acerca a la velocidad de la luz (c), se ve frenado por ese límite, y, la energía de la inercia… ¡Se convierte en masa! Eso es lo que se deduce de la fórmula E=mc2
¿Cómo que la masa aumenta con la velocidad? ¿Ahora resultará que salir a correr engorda?




La luz se propaga en el vacío a una velocidad aproximada a los 30.000 millones (3×1010) de centímetros por segundo. La cantidad c2 representa el producto c×c, es decir: 3×1010 × 3×1010, ó 9×1020. Por tanto, c2 es igual a 900.000.000.000.000.000.000. Así pues, una masa de un gramo puede convertirse, en teoría, en 9×1020 ergios de energía.
El ergio es una unida muy pequeña de energía que equivale a: “Unidad de trabajo o energía utilizado en el sistema c.g.s y actúa definida como trabajo realizado por una fuerza de 1 dina cuando actúa a lo largo de una distancia de 1 cm: 1 ergio = 10-7 julios”. La kilocaloría, de nombre quizá mucho más conocido, es igual a unos 42.000 millones de ergios. Un gramo de materia convertido en energía daría 2’2 × 1010 (22 millones) de kilocalorías. Una persona puede sobrevivir cómodamente con 2.500 kilocalorías al día, obtenidas de los alimentos ingeridos. Con la energía que representa un solo gramo de materia tendríamos reservas para unos 24.110 años, que no es poco para la vida de un hombre.

O dicho de otro modo: si fuese posible convertir en energía eléctrica la energía representada por un solo gramo de materia, bastaría para tener luciendo continuamente una bombilla de 100 vatios durante unos 28.200 años.

Claro que la luz, también es mucho más que todo eso y es una manifestación electromagnética como el resto de las radiaciones. A medida que la luz va desde una galaxia a otra más distante, esa luz se extiende como lo hace el espacio y eso hace que la luz, cuya longitud de onda es intrínsecamente corta, se convierta gradualmente en luz roja de longitud de onda más larga. Esa es la causa del desplazamiento hacia el rojo de los espectros de luz de las galaxias distantes.

¿Cómo se convierte el “desplazamiento hacia el rojo” en una manera para medir distancias en el Universo? Todo se debe a un sorprendente descubrimiento realizado en 1926 en el observatorio del monte Wilson, cerca de Los Ángeles. Allí Edwin Hubble descubrió que el Universo se está expandiendo. Fue un hallazgo increíble, pues nadie se esperaba algo así. Al haber “desplazamientos hacia el rojo” en todas direcciones, Hubble descubrió que todas las galaxias distantes del Universo se estaban separando entre sí, algo que hoy sabemos que está causado por la expansión del propio espacio.

Vista desde la Tierra una galaxia no parece alejarse, pero sabemos que sí ocurre porque su luz en espectro aparece más desplazada hacia la zona del rojo de lo habitual para los elementos químicos que nos llegan de la misma. Una galaxia que se aleje a poca velocidad adquirirá un ligero tono rojizo, pero una galaxia que se aleje más rápidamente adquirirá un rojo más intenso, un mayor “desplazamiento hacia el rojo”. Pero Hubble también descubrió que las galaxias que se mueven a mayor velocidad, también son las que están más alejadas. Eso significa que cuanto mayor sea el “desplazamiento hacia el rojo”, más lejos estará la galaxia.
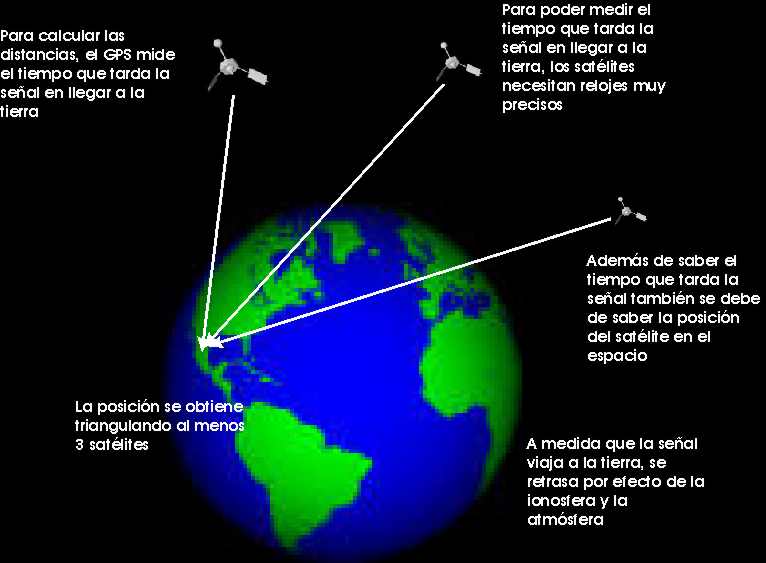
El GPS consta de una red de 24 satélites, que orbitan en la Tierra a una altura de 20000 km sobre la superficie. En cualquier momento, cualquier vehículo donde se halle instalado recibe la señal de al menos 4 satélites y compara la duración de las distancias a que se encuentran, a la velocidad de la luz, para calcular su ubicación exacta en la superficie. Todo el sistema depende de relojes extraordinariamente precisos y cuando los ingenieros los diseñaron sabían que los satélites se moverían a casi 11300 km/h, una velocidad suficiente para ralentizar sus relojes una diminuta fracción de segundo. Los ingenieros incluyeron en el sistema todas las diferencias de tiempo relativistas y eso les ha conferido una precisión impresionante. Como los relojes de los satélites avanzan a unas velocidades diferentes que los relojes situados sobre la Tierra, sin estas correcciones relativistas la posición del vehículo sería errónea.

La distorsión del tiempo es sólo una de las extrañas consecuencias de viajar con velocidades próximas a las de la luz. Imaginemos que continuamos con la “bici” pedaleando a velocidades próximas a las de la luz, entonces el espacio comienza a hacer cosas extrañas para el ciclista y para la bicicleta. Un observador apreciaría que la longitud de la bicicleta disminuye en la dirección del movimiento, que se encoge en dicha dirección. Este efecto se conoce como “contracción de la longitud” y junto con la “dilatación del tiempo” son percibidos así por un observador inmóvil cuando ve algo que se mueve con velocidades próximas a la de la luz.

Cuanto más rápido viajan, los relojes marcan el tiempo cada vez más lento. En teoría, entonces, para objetos que viajen a la velocidad de la luz… ¡El tiempo se volvería infinito y se detendría?



Aún nos enfrentamos a la velocidad de la luz como un muro impenetrable. Una velocidad que según Einstein nunca podrá ser rebasada. Sin embargo la Historia está llena de imposibles que se hicieron realidad. Por ejemplo, ¿seremos capaces de alcanzar las estrellas en naves que viajen más rápidas que la velocidad de la luz? Y si es así, ¿cuándo?

Esta sería una manera de burlar la velocidad de la luz, no de vencerla

:format(jpg)/f.elconfidencial.com%2Foriginal%2F07f%2Ffbb%2F1e0%2F07ffbb1e07ee52801d6b4b15885e432a.jpg)

Oct
28
Teorías, masas, partículas, dimensiones…
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)


Una nos habla del Cosmos y de como el espacio se curva ante la presencia de masas, la otra, nos habla de funciones de ondas, entrelazamientos cuánticos, de diminutos objetos que conforman la materia y hacen posibles los átomos y la vida.
Entre los teóricos, el casamiento de la relatividad general y la teoría cuántica es el problema central de la física moderna. A los esfuerzos teóricos que se realizan con ese propósito se les llama “super-gravedad”, “super-simetría”, “supercuerdas” “teoría M” o, en último caso, “teoría de todo o gran teoría unificada”.

La vida entre chinches del genio Perelman, el ruso que rechazó el millón de dólares del ‘nobel de las matemáticas’.
Los vecinos alucinados: “Que acepte y reparta la pasta, por lo menos”. Vive en el bloque de pisos donde reside con su madre en “el Bronx de San Petesburgo, y, en sus ratos libres, coge un canasto y un gancho y los vecinos lo ven caminar al campo para coger setas. Extraño personaje.
Uno de los logros más destacados de Perelman fue la resolución de la famosa Conjetura de Poincaré, un problema que desconcertó a los matemáticos durante más de un siglo y que se considera uno de los Problemas del Milenio, de hecho, el único de los siete que está resuelto.
Pero sigamos con lo que decíamos: “Entre los teóricos, el casamiento de la relatividad general y la teoría cuántica es el problema central de la física moderna. A los esfuerzos teóricos que se realizan con ese propósito se les llama “super-gravedad”, “super-simetría”, “supercuerdas” “teoría M” o, en último caso, “teoría de todo o gran teoría unificada”.”
Ahí tenemos unas matemáticas exóticas que ponen de punta hasta los pelos de las cejas de algunos de los mejores matemáticos del mundo (¿y Perelman? ¿Por qué nos se ha implicado?). Hablan de 10, 11 y 26 dimensiones, siempre, todas ellas espaciales menos una que es la temporal. Vivimos en cuatro: tres de espacio (este-oeste, norte-sur y arriba-abajo) y una temporal. No podemos, ni sabemos o no es posible instruir, en nuestro cerebro (también tridimensional), ver más dimensiones. Pero llegaron Kaluza y Klein y compactaron, en la longitud de Planck las dimensiones que no podíamos ver. ¡Problema solucionado!
La longitud de Planck (ℓP) u hodón (término acuñado en 1926 por Robert Lévi) es la distancia o escala de longitud por debajo de la cual se espera que el espacio deje de tener una geometría clásica. Una medida inferior previsiblemente no puede ser tratada adecuadamente en los modelos de física actuales debido a la aparición de efectos de Gravedad Cuántica.
¿Quién puede ir a la longitud de Planck para “verla”? A distancias comparables con la longitud de Planck, se cree que están sucediendo cosas muy curiosas que rebasan ampliamente los límites de nuestra imaginación. A diferencia de la filosofía reduccionista que propone que lo más complejo está elaborado -axiomáticamente- a partir de lo más elemental, lo que está sucediendo en la escala de Planck no parece tener nada de elemental o sencillo.


Qué es la longitud de Planck y por qué marca un límite en nuestra comprensión del Universo.
Al pensar en el Universo, nuestra mente tiende a irse a lo inimaginablemente inmenso, un espacio sin fronteras conocidas donde existe todo.
Sin embargo, es lo inimaginablemente diminuto lo que constituye las piedras angulares de esa inmensidad y ofrece la oportunidad de comprender cómo funciona.
Observando cómo se comportan sus componentes en las escalas más mínimas posibles podremos entender cómo se unen para crear este mundo y más.
Esa es una de las principales razones por las que hemos querido saber qué es lo más pequeño del mundo.
Y la respuesta a esa eterna pregunta ha evolucionado junto con la humanidad.
“La longitud de Planck es la única escala de distancias que puede obtenerse de manera natural a partir de las constantes de la naturaleza. Son varios los argumentos que implican que, a la escala de Planck, los efectos de la gravedad y los de la mecánica cuántica deberían combinarse, por lo que cualquier experimento que permitiesen explorar las leyes de la física a tales distancias supondría un avance tremendo en física teórica. El problema reside en su ínfimo valor, del orden de 10-35metros. En los experimentos de física de partículas, sondear distancias cada vez más pequeñas requiere emplear energías más y más elevadas. Sin embargo, la energía necesaria para escudriñar la longitud de Planck se halla muchos órdenes de magnitud por encima de las posibilidades técnicas de los aceleradores presentes o futuros. La escala de distancias que podrá explorar el LHC, por ejemplo, puede estimarse en unos 10-19 metros.”

En ese lugar nos encontramos con una especie de espuma cuántica
Se cree que a esta escala la continuidad del espacio-tiempo en vez de ir marchando sincronizadamente al parejo con lo que vemos en el macrocosmos de hecho está variando a grado tal que a nivel ultra-microscópico el tiempo no sólo avanza o se detiene aleatoriamente sino inclusive marcha hacia atrás, una especie de verdadera máquina del tiempo. Las limitaciones de nuestros conocimientos sobre las rarezas que puedan estar ocurriendo en esta escala en el orden de los 10-35 metros, la longitud de Planck, ha llevado a la proposición de modelos tan imaginativos y tan exóticos como la teoría de la espuma cuántica que supuestamente veríamos aún en la ausencia de materia-energía si fuésemos ampliando sucesivamente una porción del espacio-tiempo plano.

La exploración enigmática las dimensiones más altas. ¿No será otra solución como la que dió lugar al problema de la expansión de las galaxias, y, surgió la “materia oscura”?
La puerta de las dimensiones más altas quedó abierta y, a los teóricos, se les regaló una herramienta maravillosa. En el Hiperespacio, todo es posible. Hasta el matrimonio de la relatividad general y la mecánica cuántica, allí si es posible encontrar esa soñada teoría de la Gravedad cuántica.
Así que, los teóricos, se han embarcado a la búsqueda de un objetivo audaz: buscan una teoría que describa la simplicidad primigenia que reinaba en el intenso calor del universo en sus primeros tiempos, una teoría carente de parámetros, donde estén presentes todas las respuestas. Todo debe ser contestado a partir de una ecuación básica.
¿Dónde radica el problema?
El problema está en que la única teoría candidata no tiene conexión directa con el mundo de la observación, o no lo tiene todavía si queremos expresarnos con propiedad. La energía necesaria para ello, no la tiene ni el nuevo acelerador de partículas LHC que mencioné en páginas anteriores.
La verdad es que, la teoría que ahora tenemos, el Modelo Estándar, concuerda de manera exacta con todos los datos a bajas energías y contesta cosas sin sentido a altas energías.
¡Necesitamos algo más avanzado!
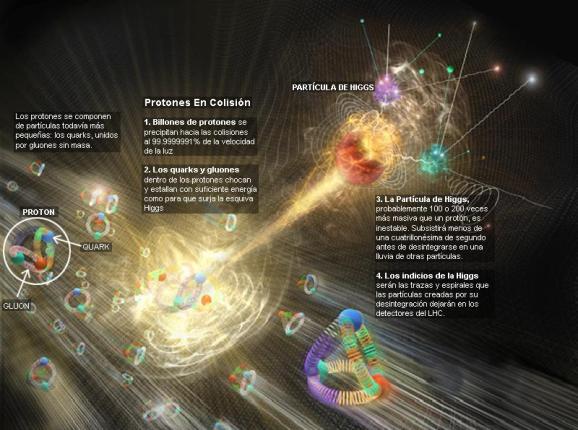
Cada partícula tiene encomendada una misión, la de Higgs, ya sabemos lo que dicen por ahí.
Se ha dicho que la función de la partícula de Higgs es la de dar masa a las Cuando su autor lanzó la idea al mundo, resultó además de nueva muy extraña. El secreto de todo radica en conseguir la simplicidad: el átomo resulto ser complejo lleno de esas infinitesimales partículas electromagnéticas que bautizamos con el nombre de electrones, resultó que tenía un núcleo que contenía, a pesar de ser tan pequeño, casi toda la masa del átomo. El núcleo, tan pequeño, estaba compuesto de otros objetos más pequeños aún, los quarks que estaban instalados en nubes de otras partículas llamadas gluones y, ahora, queremos continuar profundizando, sospechamos, que después de los quarks puede haber algo más.

Bueno, la idea nueva que surgió es que el espacio entero contiene un campo, el campo de Higgs, que impregna el vacío y es el mismo en todas partes. Es decir, que si miramos a las estrellas en una noche clara estamos mirando el campo de Higgs. Las partículas influidas por este campo, toman masa. Esto no es por sí mismo destacable, pues las partículas pueden tomar energía de los campos (gauge) de los que hemos comentado, del campo gravitatorio o del electromagnético. Si llevamos un bloque de plomo a lo alto de la Torre Eiffel, el bloque adquiriría energía potencial a causa de la alteración de su posición en el campo gravitatorio de la Tierra.
ADEMÁS DE SU BELLEZA… ¡DICEN TANTO CON TAN POCO!
Cuando los físicos hablan de la belleza de algunas ecuaciones, se refieren a las que, como ésta, dicen mucho con muy pocos caracteres. De hecho, puede que ésta sea la ecuación más famosa conocida en nuestro mundo.
Como E=mc2, ese aumento de la energía potencial equivale a un aumento de la masa, en este caso la masa del Sistema Tierra-bloque de plomo. Aquí hemos de añadirle amablemente un poco de complejidad a la venerable ecuación de Einstein. La masa, m, tiene en realidad dos partes. Una es la masa en reposo, m0, la que se mide en el laboratorio cuando la partícula está en reposo. La partícula adquiere la otra parte de la masa en virtud de su movimiento (como los protones en el acelerador de partículas, o los muones, que aumentan varias veces su masa cuando son lanzados a velocidades cercanas a c) o en virtud de su energía potencial de campo. Vemos una dinámica similar en los núcleos atómicos. Por ejemplo, si separamos el protón y el neutrón que componen un núcleo de deuterio, la suma de las masas aumenta.
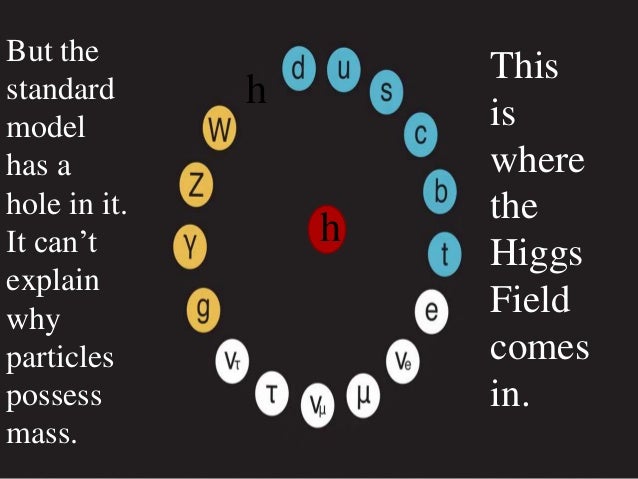

Pero la energía potencial tomada del campo de Higgs difiere en varios aspectos de la acción de los campos familiares. La masa tomada de Higgs es en realidad masa en reposo. De hecho, en la que quizá sea la versión más apasionante de la teoría del campo de Higgs, éste genera toda la masa en reposo. Otra diferencia es que la cantidad de masa que se traga del campo es distinta para las distintas partículas.
Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan éstas al campo de Higgs.
La influencia de Higgs en las masas de los quarks y de los leptones, nos recuerda el descubrimiento por Pieter Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.
Hasta hace bien poco no teniamos ni idea de que reglas controlan los incrementos de masa generados por el Higgs (de ahí la expectación creada por el nuevo acelerador de partículas LHC cuando la buscaba). Pero el problema es irritante: ¿por qué sólo esas masas -Las masas de los W+, W–, y Zº, y el up, el down, el encanto, el extraño, el top y el bottom, así como los leptones – que no forman ningún patrón obvio?

Las masas van de la del electrón 0’0005 GeV, a la del top, que tiene que ser mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electrodébil (Weinberg-salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnéticas y débiles. En la unidad hay cuatro partículas mensajeras sin masa -los W+, W–, Zº y fotón que llevan la fuerza electrodébil. Además está el campo de Higgs, y, rápidamente, los W y Z chupan la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electrodébil se fragmenta en la débil (débil porque los mensajeros son muy gordos) y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen los teóricos. Prefiero la descripción según la cual el Higgs oculta la simetría con su poder dador de masa.
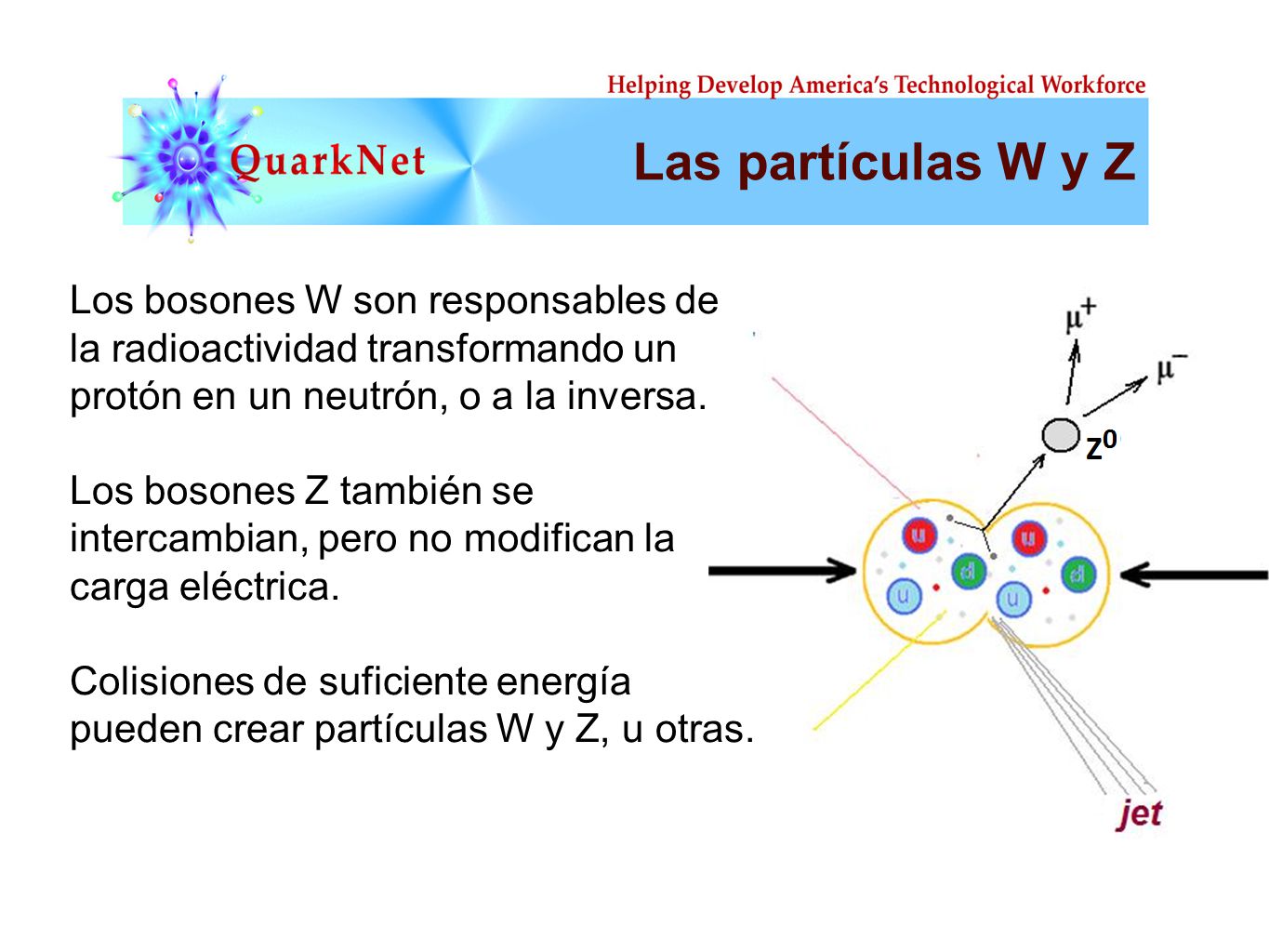
Las masas de los W y el Z se predijeron con éxito a partir de los parámetros de la teoría electrodébil. Y las relajadas sonrisas de los físicos teóricos nos recuerdan que Gerard ^t Hooft y Veltman dejaron sentado que la teoría entera esta libre de infinitos.
Pero, encierra tantos misterios la materia que, a veces me hace pensar en que la podríamos denominar de cualuquier manera menos de inerte ¡Parece que la materia está viva!
Son muchas las cosas que desconocemos y, nuestra curiosidad nos empuja continuamente a buscar esas respuestas.

El electrón y el positrón son notables por sus pequeñas masas (sólo 1/1.836 de la del protón, el neutrón, el antiprotón o antineutrón), y, por lo tanto, han sido denominados leptones (de la voz griega lentos, que significa “delgado”).
Aunque el electrón fue descubierto en 1.897 por el físico británico Josepth John Thomson (1856-1940), el problema de su estructura, si la hay, no está resuelto. Conocemos su masa y su carga negativa que responden a 9,1093897 (54) x 10-31 Kg la primera y, 1,602 177 33 (49) x 10-19 culombios, la segunda, y también su radio clásico: r0 = e2/mc2 = 2’82 x 10-13 m. No se ha descubierto aún ninguna partícula que sea menos cursiva que el electrón (o positrón) y que lleve una carga eléctrica, sea lo que fuese (sabemos como actúa y cómo medir sus propiedades, pero aun no sabemos qué es), tenga asociada un mínimo de masa, y que esta es la que se muestra en el electrón.
Lo cierto es que, el electrón, es una maravilla en sí mismo. El Universo no sería como lo conocemos si el electrón (esa cosita “insignificante”), fuese distinto a como es, bastaría un cambio infinitesimal para que, por ejemplo, nosotros no pudiéramos estar aquí ahora.

¡No por pequeño, se es insignificante!
Recordémoslo, todo lo grande está hecho de cosas pequeñas.
En realidad, existen partículas que no tienen en absoluto asociada en ellas ninguna masa (es decir, ninguna masa en reposo). Por ejemplo, las ondas de luz y otras formas de radiación electromagnéticas se comportan como partículas (Einstein en su efecto fotoeléctrico y De Broglie en la difracción de electrones*.
Esta manifestación en forma de partículas de lo que, de ordinario, concebimos como una onda se denomina fotón, de la palabra griega que significa “luz”.

El fotón tiene una masa de 1, una carga eléctrica de o, pero posee un espín de 1, por lo que es un bosón. ¿Cómo se puede definir lo que es el espín? Los fotones toman parte en las reacciones nucleares, pero el espín total de las partículas implicadas antes y después de la reacción deben permanecer inmutadas (conservación del espín). La única forma que esto suceda en las reacciones nucleares que implican a los fotones radica en suponer que el fotón tiene un espín de 1. El fotón no se considera un leptón, puesto que este termino se reserva para la familia formada por el electrón, el muón y la partícula Tau con sus correspondientes neutrinos: Ve, Vu y VT.
Existen razones teóricas para suponer que, cuando las masas se aceleran (como cuando se mueven en órbitas elípticas en torno a otra masa o llevan a cabo un colapso gravitacional), emiten energía en forma de ondas gravitacionales. Esas ondas pueden así mismo poseer aspecto de partícula, por lo que toda partícula gravitacional recibe el nombre de gravitón.

La fuerza electromagnética afecta los cuerpos eléctricamente cargados y es la fuerza involucrada en las transformaciones físicas y químicas de átomos y moléculas. Es mucho más intensa que la fuerza gravitatoria, tiene dos sentidos (positivo y negativo) y su alcance es infinito.
La fuerza gravitatoria es mucho, mucho más débil que la fuerza electromagnética. Un protón y un electrón se atraen gravitacionalmente con sólo 1/1039 de la fuerza en que se atraen electromagnéticamente. El gravitón (aún sin descubrir) debe poseer, correspondientemente, menos energía que el fotón y, por tanto, ha de ser inimaginablemente difícil de detectar.
De todos modos, el físico norteamericano Joseph Weber emprendió en 1.957 la formidable tarea de detectar el gravitón. Llegó a emplear un par de cilindros de aluminio de 153 cm. De longitud y 66 de anchura, suspendidos de un cable en una cámara de vacío. Los gravitones (que serían detectados en forma de ondas), desplazarían levemente esos cilindros, y se empleó un sistema para detectar el desplazamiento que llegare a captar la cienmillonésima parte de un centímetro.


Han llevado años captarlas, las ondas gravitatorias llevadas por el gravitón son débiles
Las débiles ondas de los gravitones, que producen del espacio profundo, deberían chocar contra todo el planeta, y los cilindros separados por grandes distancias se verán afectados de forma simultánea. En 1.969, Weber anunció haber detectado los efectos de las ondas gravitatorias. Aquello produjo una enorme excitación, puesto que apoyaba una teoría particularmente importante (la teoría de Einstein de la relatividad general). Desgraciadamente, nunca se pudo comprobar mediante las pruebas realizadas por otros equipos de científicos que duplicaran el hallazgo de Weber.
De todas formas, no creo que, a estas alturas, nadie pueda dudar de la existencia de los gravitones, el bosón mediador de la fuerza gravitatoria. La masa del gravitón es o, su carga es o, y su espín de 2. Como el fotón, no tiene antipartícula, ellos mismos hacen las dos versiones.

Tenemos que volver a los que posiblemente son los objetos más misteriosos de nuestro Universo: Los agujeros negros. Si estos objetos son lo que se dice (no parece que se pueda objetar nada en contrario), seguramente serán ellos los que, finalmente, nos faciliten las respuestas sobre las ondas gravitacionales y el esquivo gravitón.
La onda gravitacional emitida por el agujero negro produce una ondulación en la curvatura del espacio-temporal que viaja a la velocidad de la luz transportada por los gravitones.

Hay aspectos de la física que me dejan totalmente sin habla, me obligan a pensar y me transporta de este mundo material nuestro a otro fascinante donde residen las maravillas del Universo. Hay magnitudes asociadas con las leyes de la gravedad cuántica. La longitud de Planck-Wheeler, ![]() es la escala de longitud por debajo de la cual el espacio tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro.
es la escala de longitud por debajo de la cual el espacio tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro.
Me llama poderosamente la atención lo que conocemos como las fluctuaciones de vacío, esas oscilaciones aleatorias, impredecibles que no se pueden eliminar de un campo (electromagnético o gravitatorio), que son debidas a un tira y afloja en el que pequeñas regiones del espacio toman prestada momentáneamente energía de regiones adyacentes y luego la devuelven.

Ordinariamente, definimos el vacío como el espacio en el que hay una baja presión de un gas, es decir, relativamente pocos átomos o moléculas. En ese sentido, un vacío perfecto no contendría ningún átomo o molécula, pero no se puede obtener, ya que todos los materiales que rodean ese espacio tienen una presión de vapor finita. En un bajo vacío, la presión se reduce hasta 10-2 pascales, mientras que un alto vacío tiene una presión de 10-2-10-7 pascales. Por debajo de 10-7 pascales se conoce como un vacío ultraalto.
No puedo dejar de referirme al vacío theta (vació θ) que, es el estado de vacío de un campo gauge no abeliano (en ausencia de campos fermiónicos y campos de Higgs).

El vacío theta es el punto de partida para comprender el estado de vacío de las teoría gauge fuertemente interaccionantes, como la cromodinámica cuántica. En el vacío theta hay un número infinito de estados degenerados con efecto túnel entre estos estados. Esto significa que el vacío theta es análogo a una fundón de Bloch* en un cristal.
Se puede derivar tanto como un resultado general o bien usando técnicas de instantón. Cuando hay un fermión sin masa, el efecto túnel entre estados queda completamente suprimido.
Cuando hay campos fermiónicos con masa pequeña, el efecto túnel es mucho menor que para campos gauge puros, pero no está completamente suprimido.

Nos podríamos preguntar miles de cosas que no sabríamos contestar. Nos maravillan y asombran fenómenos naturales que ocurren ante nuestros ojos pero que tampoco sabemos, en realidad, a que son debidos. Si, sabemos ponerles etiquetas como, por ejemplo, la fuerza nuclear débil, la fisión espontánea que tiene lugar en algunos elementos como el protactinio o el torio y, con mayor frecuencia, en los elementos que conocemos como transuránicos y que son:
- 93 neptunio Np
- 94 plutonio Pu
- 95 americio Am
- 96 curio Cm
- 97 berkelio Bk
- 98 californio Cf
- 99 einstenio Es
- 100 fermio Fm
- 101 mendelevio Md
- 102 nobelio No
- 103 lawrencio Lr
- elementos transactínidos
- 104 rutherfordio Rf
- 105 dubnio Db
- 106 seaborgio Sg
- 107 bohrio Bh
- 108 hassio Hs
- 109 meitnerio Mt
- 110 darmstadtio Ds
- 111 roentgenio Rg
- 112 copernicio Cn
- 113 nihonio Nh
- 114 flerovio Fl
- 115 moscovio Mc
- 116 livermorio Lv
- 117 teneso Ts
- 118 oganesón Og
Los elementos transuránicos o elementos transuránidos son elementos químicos con número atómico mayor que 92, el número atómico del elemento uranio. El nombre de trans-uránidos significa «más allá del uranio». Posición en la tabla periódica del uranio.
A medida que los núcleos se hacen más grandes, la probabilidad de una fisión espontánea aumenta. En los elementos más pesados de todos (einstenio, fermio y mendelevio), esto se convierte en el método más importante de ruptura, sobre pasando a la emisión de partículas alfa.
Emilio Silvera Vázquez
Oct
26
El Electrón (el personaje más pequeño de la familia leptón)
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)

Sí, el electrón es el más pequeño de la familia si no tenemos en cuenta los neutrinos acompañantes
En esta representación artística, un electrón orbita el núcleo de un átomo, girando alrededor de su eje mientras una nube de otras partículas subatómicas se emiten y reabsorben constantemente – Nicolle R. Fuller, Fundación Nacional de Ciencia
El Electrón sigue siendo la esfera más perfecta del Universo
El examen de esta partícula elemental con una precisión sin precedentes respalda, una vez más, el modelo estándar de la física
Investigadores del Imperial College de Londres concluyeron en 2011 que el electrón es la esfera más perfecta del Universo. Según anunciaron, lo que separa a esta partícula elemental de la redondez absoluta es menos de 0,000000000000000000000000001 cm, algo insignificante. En otras palabras, «si un electrón se inflara hasta el tener el tamaño del Sistema Solar, todavía parecería esférico».
Ahora, investigadores de las universidades estadounidenses de Northwestern, Harvard y Yale han examinado nuevamente la forma de la carga del electrón con una precisión sin precedentes. Y nada ha cambiado. Los investigadores han confirmado que es perfectamente esférico. Esta conclusión va mucho más allá de una mera curiosidad científica. Una carga ligeramente aplastada podría haber indicado partículas pesadas desconocidas y difíciles de detectar a su alrededor, un descubrimiento que, de haberse producido, habría afectado a la comunidad física mundial. Sin embargo, y aunque para algunos puede resultar decepcionante, todo parece seguir el guion del modelo estándar, la teoría que describe cómo funciona el Universo y que, pese a sus lagunas evidentes, todavía no ha podido ser desbancada.

Representación de un electrón- Nicolle R. Fuller, Fundación Nacional de Ciencia
«Si hubiéramos descubierto que la forma no era redonda, ese sería el mayor titular en física de las últimas décadas», dice Gerald Gabrielse, quien dirigió la investigación en Northwestern. «Pero nuestro descubrimiento sigue siendo igual de importante científicamente porque fortalece el modelo estándar de la física de partículas y excluye modelos alternativos». El estudio aparece publicado en la revista «Nature».
El modelo estándar describe la mayoría de las fuerzas y partículas fundamentales en el universo. Es una imagen matemática de la realidad, y ningún experimento de laboratorio realizado ha sido capaz de contradecirlo por el momento. Pero eso ha sido desconcertante para los físicos durante décadas. «El modelo estándar tal como está no puede ser correcto porque no puede predecir por qué existe el Universo», señala Gabrielse, profesor de física. «Esa es una laguna bastante grande».
Supersimetría
Al tratar de «arreglar» el modelo estándar, muchos modelos alternativos predicen que la esfera aparentemente uniforme de un electrón está en realidad aplastada asimétricamente. Uno de esos modelos, llamado supersimetría, postula que partículas subatómicas pesadas y desconocidas influyen en el electrón para alterar su forma perfectamente esférica, un fenómeno no probado llamado «momento dipolar eléctrico». Estas partículas más pesadas y sin descubrir podrían ser responsables de algunos de los misterios más deslumbrantes del Universo y posiblemente podrían explicar por qué está hecho de materia en lugar de antimateria.
«Casi todos los modelos alternativos dicen que la carga de electrones podría estar aplastada, pero simplemente no lo hemos visto con suficiente sensibilidad», apunta Gabrielse. «Es por eso que decidimos mirar allí con una precisión más alta de lo que nunca antes se había observado».

Crean un microscopio capaz de “ver” electrones en movimiento
Investigadores de la Universidad de Arizona desarrollan el microscopio más rápido del mundo que abre nuevas fronteras en la observación de procesos electrónicos ultrarrápidos.
En física, el electrón, comúnmente representado por el símbolo e−, es una partícula subatómica con una carga eléctrica elemental negativa. Un electrón no tiene componentes o subestructura conocidos; en otras palabras, generalmente se define como una partícula elemental.
Con este objetivo en mente, el equipo disparó un haz de moléculas de óxido de torio frías a una cámara del tamaño de un escritorio grande. Luego, los investigadores estudiaron la luz emitida por las moléculas. Una luz torcida indicaría un momento dipolo eléctrico. Como la luz no se torció, el equipo de investigación concluyó que la forma del electrón era, de hecho, redonda, confirmando la predicción del modelo estándar. Que no haya evidencia de un momento dipolo eléctrico significa que no hay evidencia de esas partículas hipotéticas más pesadas. Y si a pesar de todo estas partículas existen, sus propiedades difieren de las predichas por los teóricos.
«Nuestro resultado le dice a la comunidad científica que necesitamos repensar seriamente algunas de las teorías alternativas», asegura David DeMille, profesor de física en Yale y coautor del estudio.
En 2014, el equipo realizó la misma medición con un aparato más simple. Al utilizar métodos mejorados y diferentes frecuencias de láser, el experimento actual era un orden de magnitud más sensible que su predecesor. «Si un electrón fuera del tamaño de la Tierra, podríamos detectar si el centro del planeta está a una distancia un millón de veces más pequeña que un cabello humano», explica Gabrielse. «Así de sensible es nuestro aparato».
Los investigadores planean seguir afinando sus instrumentos para realizar mediciones cada vez más precisas. Hasta que los investigadores encuentren evidencias de lo contrario, la forma redonda de los electrones y los misterios del universo permanecerán como están.
«Sabemos que el modelo estándar está mal, pero parece que no podemos encontrar dónde está mal. Es como una gran novela de misterio», admite Gabrielse. «Debemos ser muy cuidadosos al hacer suposiciones de que estamos más cerca de resolver el misterio, pero tengo una gran esperanza de que nos estamos acercando a este nivel de precisión».
Para saber más: Marzio Nessi, físico del CERN: «Estamos a punto de dar el salto a una nueva física».
Oct
26
Velocidades inimaginables
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
En el centro del átomo se encuentra un pequeño grano compacto aproximadamente 100.000 veces más pequeño que el propio átomo: el núcleo atómico. Su masa, e incluso más aún su carga eléctrica, determinan las propiedades del átomo del cual forma parte. Debido a la solidez del núcleo parece que los átomos, que dan forma a nuestro mundo cotidiano, son intercambiables entre sí, e incluso cuando interaccionan entre ellos para formar sustancias químicas (los elementos). Pero el núcleo, a pesar de ser tan sólido, puede partirse. Si dos átomos chocan uno contra el otro con gran velocidad podría suceder que los núcleos llegaran a chocar entre sí y entonces, o bien se rompen en trozos, o se funden liberando en el proceso partículas sub-nucleares. La nueva física de la primera mitad del siglo XX estuvo dominada por los nuevos acertijos que estas partículas planteaban.


Pero tenemos la mecánica cuántica; ¿Es que no es aplicable siempre?, ¿Cuál es la dificultad? Desde luego, la mecánica cuántica es válida para las partículas subatómicas, pero hay más que eso. Las fuerzas con que estas partículas interaccionan y que mantienen el núcleo atómico unido son tan fuertes que las velocidades a las que tienen que moverse dentro y fuera del núcleo están cerca de la velocidad de la luz, c, que es de 299.792’458 Km/s. Cuando tratamos con velocidades tan altas se necesita una segunda modificación a las leyes de la física del siglo XIX; tenemos que contar con la teoría de la relatividad especial de Einstein.

Esta teoría también fue el resultado de una publicación de Einstein de 1905. en esta teoría quedaron sentadas las bases de que el movimiento y el reposo son conceptos relativos, no son absolutos, como tampoco habrá un sistema de referencia absoluto con respecto al cual uno pueda medir la velocidad de la luz.
Pero había más cosas que tenían que ser relativas. En este teoría, la masa y la energía también dependen de la velocidad, como lo hacen la intensidad del campo eléctrico y del magnético. Einstein descubrió que la masa de una partícula es siempre proporcional a la energía que contienen, supuesto que se haya tenido en cuenta una gran cantidad de energía en reposo de una partícula cualquiera, como se denota a continuación:
E = mc2
Pero ¿por qué nada puede superar a la velocidad de la luz en el vacío?
Supongamos un objeto acelerando, ganando velocidad y acercando su velocidad a la de la luz. Según la Teoría de la relatividad la energía necesaria para acelerar este objeto irá aumentando a medida que aumenta su velocidad como si su masa aumentará según la fórmula

Es fácil ver que a medida que v aumenta y se va acercando a c el valor de la raiza cuadrada del denominador va bajando hacia cero y por lo tanto el valor de la masa m va aumentando hacia infinito. El límite de esta expresión cuando v tiende a c es infinito.
Como la velocidad de la luz es muy grande, esta ecuación sugiere que cada partícula debe almacenar una cantidad enorme de energía, y en parte esta predicción fue la que hizo que la teoría de la relatividad tuviese tanta importancia para la física (¡y para todo el mundo!). Para que la teoría de la relatividad también sea auto-consistente tiene que ser holista, esto es, que todas las cosas y todo el mundo obedezcan a las leyes de la relatividad. No son sólo los relojes los que se atrasan a grandes velocidades, sino que todos los procesos animados se comportan de la forma tan inusual que describe esta teoría cuando nos acercamos a la velocidad de la luz. El corazón humano es simplemente un reloj biológico y latirá a una velocidad menor cuando viaje en un vehículo espacial a velocidades cercanas a la de la luz. Este extraño fenómeno conduce a lo que se conoce como la “paradoja de los gemelos”, sugerida por Einstein, en la que dos gemelos idénticos tienen diferente edad cuando se reencuentran después de que uno haya permanecido en la Tierra mientras que el otro ha viajado a velocidades relativistas.
Einstein comprendió rápidamente que las leyes de la gravedad también tendrían que ser modificadas para que cumplieran el principio relativista.

La formulación de newton es bien conocida, en la segunda imagen que se representan en este esquema dos partículas que se acercan entre sí siguiendo un movimiento acelerado. La interpretación newtoniana supone que el espacio-tiempo es llano y que lo que provoca la curvatura de las líneas de universo es la fuerza de interacción gravitatoria entre ambas partículas. Por el contrario, la interpretación einsteiniana supone que las líneas de universo de estas partículas son geodésicas (“rectas”), y que es la propia curvatura del espacio tiempo lo que provoca su aproximación progresiva.
Para poder aplicar el principio de la relatividad a la fuerza gravitatoria, el principio tuvo que ser extendido de la siguiente manera: no sólo debe ser imposible determinar la velocidad absoluta del laboratorio, sino que también es imposible distinguir los cambios de velocidad de los efectos de una fuerza gravitatoria.

Einstein comprendió que la consecuencia de esto era que la gravedad hace al espacio-tiempo lo que la humedad a una hoja de papel: deformar la superficie con desigualdades que no se pueden eliminar. Hoy en día se conocen muy bien las matemáticas de los espacios curvos, pero en el época de Einstein el uso de estas nociones matemáticas tan abstractas para formular leyes físicas era algo completamente nuevo, y le llevó varios años encontrar la herramienta matemática adecuada para formular su teoría general de la relatividad que describe cómo se curva el espacio en presencia de grandes masas como planetas y estrellas.

Einstein tenía la idea en su mente desde 1907 (la relatividad especial la formuló en 1905), y se pasó 8 años buscando las matemáticas adecuadas para su formulación.
Leyendo el material enviado por un amigo al que pidió ayuda, Einstein quedó paralizado. Ante él, en la primera página de una conferencia dada ante el Sindicato de Carpinteros, 60 años antes por un tal Riemann, tenía la solución a sus desvelos: el tensor métrico de Riemann, que le permitiría utilizar una geometría espacial de los espacios curvos que explicaba su relatividad general.

Desde que se puso en órbita el telescopio espacial de rayos gamma Fermi, el 11 de junio de 2008, ha detectado poblaciones enteras de objetos nunca antes vistos. El último hallazgo de Fermi afecta al púlsar J1823-3021A, avistado en 1994 con el radiotelescopio Lovell, en Inglaterra. Un equipo internacional de expertos se ha dado cuenta de que esta estrella pulsante emite rayos gamma y gracias a Fermi ha podido caracterizar sus inusuales propiedades. Los resultados de su investigación se publican en el último número de Science. Lo cierto es que han descubierto el púlsar de milisegundos más joven y con la fuerza magnética más potente

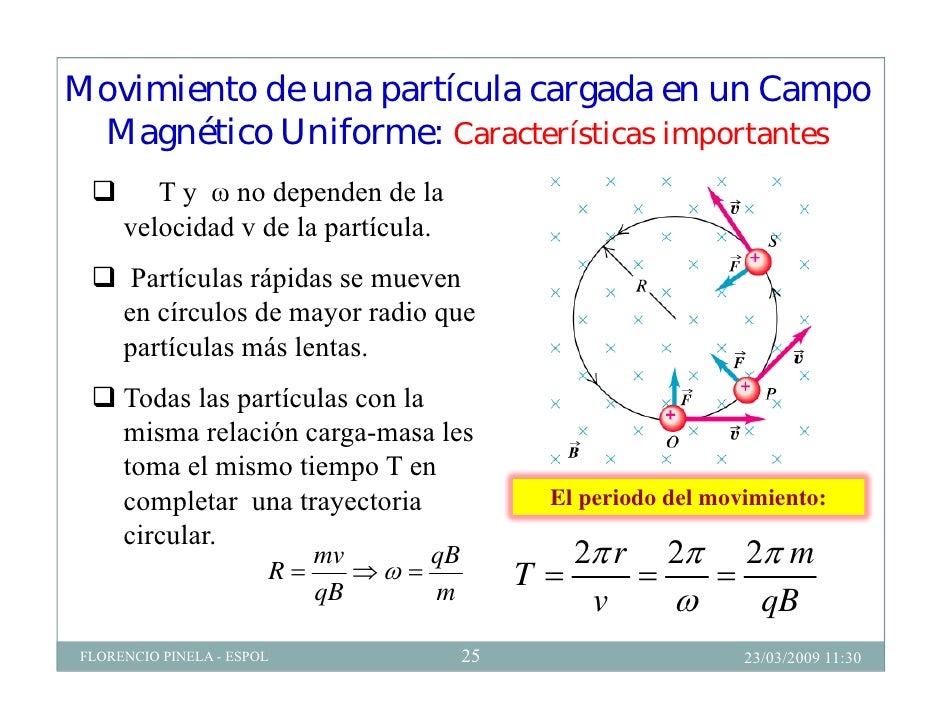
No está mal que en este punto recordemos la fuerza magnética y gravitatoria que nos puede ayudar a comprender mejor el comportamiento de las partículas subatómicas.
El electromagnetismo, decíamos al principio, es la fuerza con la cual dos partículas cargadas eléctricamente se repelen (si sus cargas son iguales) o se atraen (si tienen cargas de signo opuesto).
La interacción magnética es la fuerza que experimenta una partícula eléctricamente cargada que se mueve a través de un campo magnético. Las partículas cargadas en movimiento generan un campo magnético como, por ejemplo, los electrones que fluyen a través de las espiras de una bobina.
Las fuerzas magnéticas y eléctricas están entrelazadas. En 1873, James Clerk Maxwell consiguió formular las ecuaciones completas que rigen las fuerzas eléctricas y magnéticas, descubiertas experimentalmente por Michael Faraday. Se consiguió la teoría unificada del electromagnetismo que nos vino a decir que la electricidad y el magnetismo eran dos aspectos de una misma cosa.


La interacción es universal, de muy largo alcance (se extiende entre las estrellas), es bastante débil. Su intensidad depende del cociente entre el cuadrado de la carga del electrón y 2hc (dos veces la constante de Planck por la velocidad de la luz). Esta fracción es aproximadamente igual a 1/137’036…, o lo que llamamos α y se conoce como constante de estructura fina.
En general, el alcance de una interacción electromagnética es inversamente proporcional a la masa de la partícula mediadora, en este caso, el fotón, sin masa.
También antes hemos comentado sobre la interacción gravitatoria de la que Einstein descubrió su compleja estructura y la expuso al mundo en 1915 con el nombre de teoría general de la relatividad, y la relacionó con la curvatura del espacio y el tiempo. Sin embargo, aún no sabemos cómo se podrían reconciliar las leyes de la gravedad y las leyes de la mecánica cuántica (excepto cuando la acción gravitatoria es suficientemente débil).

La teoría de Einstein nos habla de los planetas y las estrellas del cosmos. La teoría de Planck, Heisemberg, Schrödinger, Dirac, Feynman y tantos otros, nos habla del comportamiento del átomo, del núcleo, de las partículas elementales en relación a estas interacciones fundamentales. La primera se ocupa de los cuerpos muy grandes y de los efectos que causan en el espacio y en el tiempo; la segunda de los cuerpos muy pequeños y de su importancia en el universo atómico. Cuando hemos tratado de unir ambos mundos se produce una gran explosión de rechazo. Ambas teorías son (al menos de momento) irreconciliables.

La Gravedad es la más débil de las cuatro fuerzas fundamentales
- La interacción gravitatoria actúa exclusivamente sobre la masa de una partícula.
- La gravedad es de largo alcance y llega a los más lejanos confines del universo conocido.
- Es tan débil que, probablemente, nunca podremos detectar esta fuerza de atracción gravitatoria entre dos partículas elementales. La única razón por la que podemos medirla es debido a que es colectiva: todas las partículas (de la Tierra) atraen a todas las partículas (de nuestro cuerpo) en la misma dirección.
El minúsculo y juguetón “gravitón” se ríe de todos y juega al escondite con los físicos del mundo

Un equipo de científicos asegura que, por primera vez en la histroria, está cerca de ver un gravitón, la partícula cuántica teórica de la gravedad
La partícula mediadora es el hipotético gravitón. Aunque aún no se ha descubierto experimentalmente, sabemos lo que predice la mecánica cuántica: que tiene masa nula y espín 2.
La ley general para las interacciones es que, si la partícula mediadora tiene el espín par, la fuerza entre cargas iguales es atractiva y entre cargas opuestas repulsiva. Si el espín es impar (como en el electromagnetismo) se cumple a la inversa.
Pero antes de seguir profundizando en estas cuestiones hablemos de las propias partículas subatómicas, para lo cual la teoría de la relatividad especial, que es la teoría de la relatividad sin fuerza gravitatoria, es suficiente.

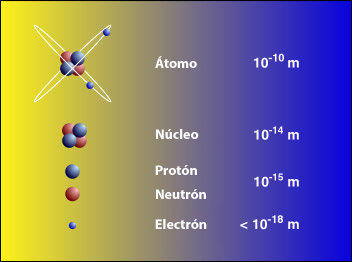
Si viajamos hacia lo muy pequeño tendremos que ir más allá de los átomos, que son objetos voluminosos y frágiles comparados con lo que nos ocupará a continuación: el núcleo atómico y lo que allí se encuentra. Los electrones, que ahora vemos “a gran distancia” dando vueltas alrededor del núcleo, son muy pequeños y extremadamente robustos. El núcleo está constituido por dos especies de bloques: protones y neutrones. El protón (del griego πρώτος, primero) debe su nombre al hecho de que el núcleo atómico más sencillo, que es el hidrógeno, está formado por un solo protón. Tiene una unidad de carga positiva. El neutrón recuerda al protón como si fuera su hermano gemelo: su masa es prácticamente la misma, su espín es el mismo, pero en el neutrón, como su propio nombre da a entender, no hay carga eléctrica; es neutro.
La masa de estas partículas se expresa en una unidad llamada mega-electrón-voltio o MeV, para abreviar. Un MeV, que equivale a 106 electrón-voltios, es la cantidad de energía de movimiento que adquiere una partícula con una unidad de carga (tal como un electrón o un protón) cuando atraviesa una diferencia de potencial de 106 (1.000.000) voltios. Como esta energía se transforma en masa, el MeV es una unidad útil de masa para las partículas elementales.
![]()

La mayoría de los núcleos atómicos contienen más neutrones que protones. Los protones se encuentran tan juntos en el interior de un núcleo tan pequeño que se deberían repeles entre sí fuertemente, debido a que tienen cargas eléctricas del mismo signo. Sin embargo, hay una fuerza que los mantiene unidos estrechamente y que es mucho más potente e intensa que la fuerza electromagnética: la fuerza o interacción nuclear fuerte, unas 102 veces mayor que la electromagnética, y aparece sólo entre hadronespara mantener a los nucleones confinados dentro del núcleo. Actúa a una distancia tan corta como 10-15 metros, o lo que es lo mismo, 0’000000000000001 metros.
La interacción fuerte está mediada por el intercambio de mesones virtuales, 8 gluones que, como su mismo nombre indica (glue en inglés es pegamento), mantiene a los protones y neutrones bien sujetos en el núcleo, y cuanto más se tratan de separar, más aumenta la fuerza que los retiene, que crece con la distancia, al contrario que ocurre con las otras fuerzas.

La luz es una manifestación del fenómeno electromagnético y está cuantizada en “fotones”, que se comportan generalmente como los mensajeros de todas las interacciones electromagnéticas. Así mismo, como hemos dejado reseñado en el párrafo anterior, la interacción fuerte también tiene sus cuantos (los gluones). El físico japonés Hideki Yukawa (1907 – 1981) predijo la propiedad de las partículas cuánticas asociadas a la interacción fuerte, que más tarde se llamarían piones. Hay una diferencia muy importante entre los piones y los fotones: un pión es un trozo de materia con una cierta cantidad de “masa”. Si esta partícula está en reposo, su masa es siempre la misma, aproximadamente 140 MeV, y si se mueve muy rápidamente, su masa parece aumentar en función E = mc2. Por el contrario, se dice que la masa del fotón en reposo es nula. Con esto no decimos que el fotón tenga masa nula, sino que el fotón no puede estar en reposo. Como todas las partículas de masa nula, el fotón se mueve exclusivamente con la velocidad de la luz, 299.792’458 Km/s, una velocidad que el pión nunca puede alcanzar porque requeriría una cantidad infinita de energía cinética. Para el fotón, toda su masa se debe a su energía cinética.
Los físicos experimentales buscaban partículas elementales en las trazas de los rayos cósmicos que pasaban por aparatos llamados cámaras de niebla. Así encontraron una partícula coincidente con la masa que debería tener la partícula de Yukawa, el pión, y la llamaron mesón (del griego medio), porque su masa estaba comprendida entre la del electrón y la del protón. Pero detectaron una discrepancia que consistía en que esta partícula no era afectada por la interacción fuerte, y por tanto, no podía ser un pión. Actualmente nos referimos a esta partícula con la abreviatura μ y el nombre de muón, ya que en realidad era un leptón, hermano gemelo del electrón, pero con 200 veces su masa.
Antes de seguir veamos las partículas elementales de vida superior a 10-20 segundos que eran conocidas en el año 1970.
| Nombre | Símbolo | Masa (MeV) | Carga | Espín | Vida media (s) |
| Fotón | γ | 0 | 0 | 1 | ∞ |
| Leptones (L = 1, B = 0) | |||||
| Electrón | e– | 0’5109990 | – | ½ | ∞ |
| Muón | μ– | 105’6584 | – | ½ | 2’1970 × 10-6 |
| Tau | τ | ||||
| Neutrino electrónico | νe | ~ 0 | 0 | ½ | ~ ∞ |
| Neutrino muónico | νμ | ~ 0 | 0 | ½ | ~ ∞ |
| Neutrino tauónico | ντ | ~ 0 | 0 | ½ | ~ ∞ |
| Mesones (L = 0, B = 0) | |||||
| Pión + | π+ | 139’570 | 2’603 × 10-8 | ||
| Pión – | π– | 139’570 | 2’603 × 10-8 | ||
| Pión 0 | π0 | 134’976 | 0’84 × 10-16 | ||
| Kaón + | k+ | 493’68 | 1’237 × 10-8 | ||
| Kaón – | k– | 493’68 | 1’237 × 10-8 | ||
| Kaón largo | kL | 497’7 | 5’17 × 10-8 | ||
| Kaón corto | kS | 497’7 | 0’893 × 10-10 | ||
| Eta | η | 547’5 | 0 | 0 | 5’5 × 10-19 |
| Bariones (L = 0, B = 1) | |||||
| Protón | p | 938’2723 | + | ½ | ∞ |
| Neutrón | n | 939’5656 | 0 | ½ | 887 |
| Lambda | Λ | 1.115’68 | 0 | ½ | 2’63 × 10-10 |
| Sigma + | Σ+ | 1.189’4 | + | ½ | 0’80 × 10-10 |
| Sigma – | Σ– | 1.1974 | – | ½ | 7’4× 10-20 |
| Sigma 0 | Σ0 | 0 | ½ | 1’48 × 10-10 | |
| Ksi 0 | Ξ0 | 1.314’9 | 0 | ½ | 2’9 × 10-10 |
| Ksi – | Ξ– | 1.321’3 | – | ½ | 1’64 × 10-10 |
| Omega – | Ω– | 1.672’4 | – | 1½ | 0’82 × 10-10 |


Para cada leptón y cada barión existe la correspondiente antipartícula, con exactamente las mismas propiedades a excepción de la carga que es la contraria. Por ejemplo, el antiprotón se simboliza con y el electrón con e+. Los mesones neutros son su propia antipartícula, y el π+ es la antipartícula del π–, al igual que ocurre con k+ y k–. El símbolo de la partícula es el mismo que el de su antipartícula con una barra encima. Las masas y las vidas medias aquí reflejadas pueden estar corregidas en este momento, pero de todas formas son muy aproximadas.
![53 - TEORÍA CUÁNTICA de CAMPOS [ ISOSPIN - SU(2) ]](https://i.ytimg.com/vi/aukgd8NBO_E/hq720.jpg?sqp=-oaymwEhCK4FEIIDSFryq4qpAxMIARUAAAAAGAElAADIQj0AgKJD&rs=AOn4CLDhPy7Cl5O2LZ8GZHAfx1mCydUPuw)
Los símbolos que se pueden ver algunas veces, como s (extrañeza) e i (isoespín) están referidos a datos cuánticos que afectan a las partículas elementales en sus comportamientos.
Debo admitir que todo esto tiene que sonar algo misterioso. Es difícil explicar estos temas por medio de la simple palabra escrita sin emplear la claridad que transmiten las matemáticas, lo que, por otra parte, es un mundo secreto para el común de los mortales, y ese lenguaje es sólo conocido por algunos privilegiados que, mediante un sistema de ecuaciones pueden ver y entender de forma clara, sencilla y limpia, todas estas complejas cuestiones.

Si hablamos del espín (o, con más precisión, el momento angular, que es aproximadamente la masa por el radio por la velocidad de rotación) se puede medir como un múltiplo de la constante de Planck, h, dividido por 2π. Medido en esta unidad y de acuerdo con la mecánica cuántica, el espín de cualquier objeto tiene que ser o un entero o un entero más un medio. El espín total de cada tipo de partícula – aunque no la dirección del mismo – es fijo.
El electrón, por ejemplo, tiene espín ½. Esto lo descubrieron dos estudiantes holandeses, Samuel Gondsmit (1902 – 1978) y George Uhlenbeck (1900 – 1988), que escribieron sus tesis conjuntamente sobre este problema en 1972. Fue una idea audaz que partículas tan pequeñas como los electronespudieran tener espín, y de hecho, bastante grande. Al principio, la idea fue recibida con escepticismo porque la “superficie del electrón” se tendría que mover con una velocidad 137 veces mayor que la de la luz, lo cual va en contra de la teoría de la relatividad general en la que está sentado que nada en el universo va más rápido que la luz, y por otra parte, contradice E=mc2, y el electrón pasada la velocidad de la luz tendría una masa infinita.
Hoy día, sencillamente, tal observación es ignorada, toda vez que el electrón carece de superficie.
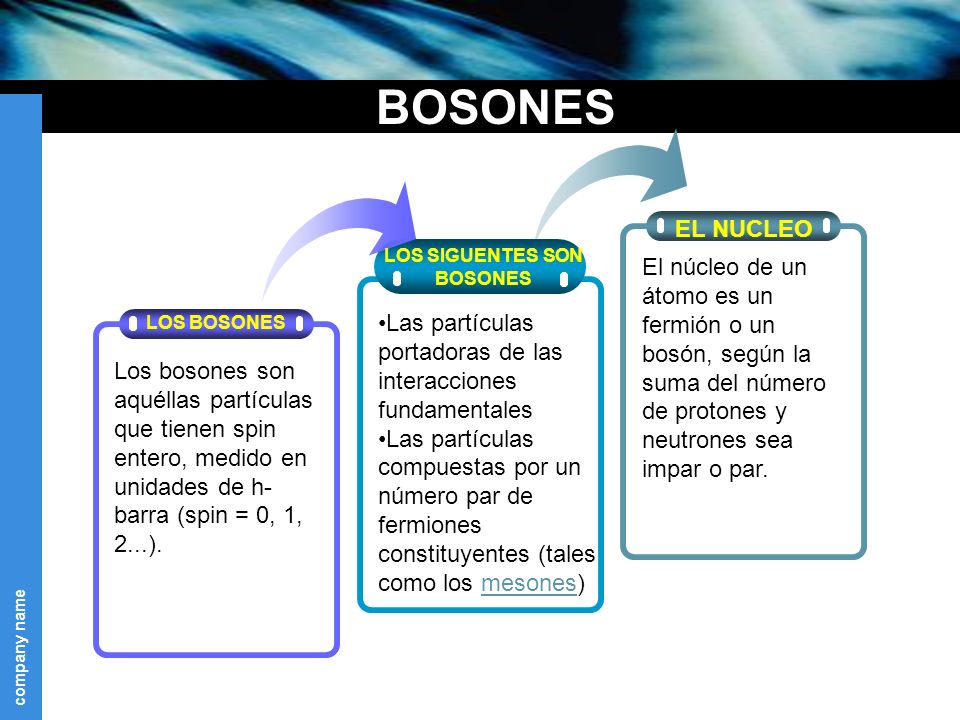

Las partículas con espín entero se llaman bosones, y las que tienen espín entero más un medio se llaman fermiones. Consultado los valores del espín en la tabla anterior podemos ver que los leptones y los bariones son fermiones, y que los mesones y los fotones son bosones. En muchos aspectos, los fermionesse comportan de manera diferente de los bosones. Los fermiones tienen la propiedad de que cada uno de ellos requiere su propio espacio: dos fermiones del mismo tipo no pueden ocupar o estar en el mismo punto, y su movimiento está regido por ecuaciones tales que se evitan unos a otros. Curiosamente, no se necesita ninguna fuerza para conseguir esto. De hecho, las fuerzas entre los fermiones pueden ser atractivas o repulsivas, según las cargas. El fenómeno por el cual cada fermión tiene que estar en un estado diferente se conoce como el principio de exclusión de Pauli. Cada átomo está rodeado de una nube de electrones, que son fermiones (espín ½). Si dos átomos se aproximan entre sí, los electrones se mueven de tal manera que las dos nubes se evitan una a otra, dando como resultado una fuerza repulsiva. Cuando aplaudimos, nuestras manos no se atraviesan pasando la uno a través de la otra. Esto es debido al principio de exclusión de Pauli para los electrones de nuestras manos que, de hecho, los de la izquierda rechazan a los de la derecha.
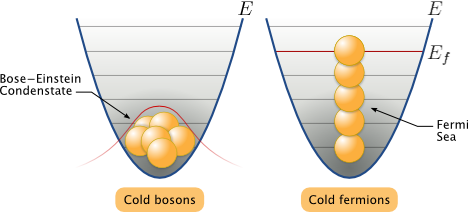
En contraste con el característico individualismo de los fermiones, los bosones se comportan colectivamente y les gusta colocarse todos en el mismo lugar. Un láser, por ejemplo, produce un haz de luz en el cual muchísimos fotones llevan la misma longitud de onda y dirección de movimiento. Esto es posible porque los fotones son bosones.
Cuando hemos hablado de las fuerzas fundamentales que, de una u otra forma, interaccionan con la materia, también hemos explicado que la interacción débil es la responsable de que muchas partículas y también muchos núcleos atómicos exóticos sean inestables. La interacción débil puede provocar que una partícula se transforme en otra relacionada, por emisión de un electrón y un neutrino. Enrico Fermi, en 1934, estableció una fórmula general de la interacción débil, que fue mejorada posteriormente por George Sudarshan, Robert Marschak, Murray Gell-Mann, Richard Feynman y otros. La fórmula mejorada funciona muy bien, pero se hizo evidente que no era adecuada en todas las circunstancias.

Uno de los protones se transmuta en un neutrón por medio de la interacción débil, transformando un quark “up”, en “down”. Este proceso consume energía (el neutrón tiene ligeramente más masa que..
En 1970, de las siguientes características de la interacción débil sólo se conocían las tres primeras:
- La interacción actúa de forma universal sobre muchos tipos diferentes de partículas y su intensidad es aproximadamente igual para todas (aunque sus efectos pueden ser muy diferentes en cada caso). A los neutrinos les afecta exclusivamente la interacción débil.
- Comparada con las demás interacciones, ésta tiene un alcance muy corto.
- La interacción es muy débil. Consecuentemente, los choques de partículas en los cuales hay neutrinos involucrados son tan poco frecuentes que se necesitan chorros muy intensos de neutrinos para poder estudiar tales sucesos.
- Los mediadores de la interacción débil, llamados W+, W– y Z0, no se detectaron hasta la década de 1980. al igual que el fotón, tienen espín 1, pero están eléctricamente cargados y son muy pesados (esta es la causa por la que el alcance de la interacción es tan corto). El tercer mediador, Z0, que es responsable de un tercer tipo de interacción débil que no tiene nada que ver con la desintegración de las partículas llamada “corriente neutra”, permite que los neutrinos puedan colisionar con otras partículas sin cambiar su identidad.
A partir de 1970, quedó clara la relación de la interacción débil y la electromagnética (electrodébil de Weinberg-Salam).
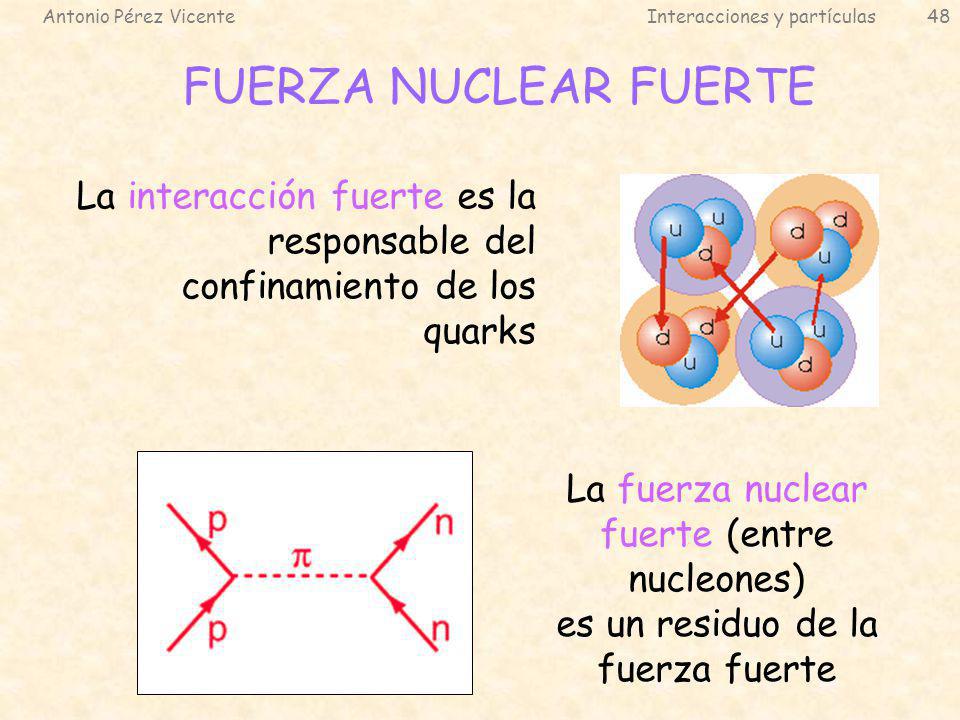
La interacción fuerte (como hemos dicho antes) sólo actúa entre las partículas que clasificamos en la familia llamada de los hadrones, a los que proporciona una estructura interna complicada. Hasta 1972 sólo se conocían las reglas de simetría de la interacción fuerte y no fuimos capaces de formular las leyes de la interacción con precisión.
Como apuntamos, el alcance de esta interacción no va más allá del radio de un núcleo atómico ligero (10-13 cm aproximadamente).

La interacción es fuerte. En realidad, la más fuerte de todas. Actúa como un muelle de Acero, cuanto más lo estiramos más se resiste. La Interacción fuerte es la única de las cuatro fuerzas que crece con la distancia. Si los Gluones se quieren separar, son agarros por los Gluones y los retienen allí confinados (son las entrañas de los nucleones).
Lo dejaré aquí, en verdad, eso que el Modelo Estándar de la Física, es feo, complejo e incompleto y, aunque hasta el momento es una buena herramienta con la que trabajar, la verdad es que, se necesita un nuevo modelo más avanzado y que incluya la Gravedad.
Y, a todo esto, esperemos que el LHC, dotado de más energía, pueda por fin encontrar al Gravitón
Emilio Silvera Vázquez
















 Totales: 72.381.412
Totales: 72.381.412 Conectados: 37
Conectados: 37