Curvatura del Espacio-Tiempo.
(Física, Astronomía y Astrofísica)

En el interior de esta libreta, en sus páginas, encontraréis las respuestas a preguntas que a veces os habéis planteado a vosotros mismos y que no han sido contestadas.

Sí; son muchos los seres que por razones muy diversas no han podido tener una educación y preparación suficientes, no han tenido la posibilidad de adquirir los conocimientos que, al menos, les diera la razón de ser de las cosas, un mínimo de saber sobre las maravillas que les rodean y que, precisamente por ignorancia, no pueden contemplar.

Desde que atemorizados mirábamos, en la tormenta, caer los rayos del cielo, oíamos los truenos que seguían a los fogonazos de los relámpagos y, hacinados en una oscura y húmeda cueva nos resguardábamos del frío y de los peligros de la noche y de los crudos días del invierno, desde entonces digo, han cambiado muchas cosas.

Será mejor que paséis al interior de estas páginas para conocer:

¿Qué es o que significa...

Curvatura del espacio-tiempo, relatividad especial y relatividad general, mecánica cuántica, partícula elemental y partícula virtual, densidad crítica y densidad media de la materia, estrella de neutrones, agujero negro, Big Bang, Big Crunch, universo plano, universo abierto o universo cerrado, la materia oscura, y la teoría de supercuerdas... entre un sin fin de preguntas más que, en alguna ocasión, os hubiera gustado que alguien os contestara.

Ahora tenéis la oportunidad de saber y conocer las respuestas a estas y otras cuestiones (para muchos misteriosas) que, en realidad, en algunos de los casos mencionados, aún hoy, nadie sabe la respuesta cierta y lo que se explicará son especulaciones y adelantos de los trabajos realizados.

Hay que entender, cuando hablamos de curvatura del espacio-tiempo, que estamos describiendo el universo en cuatro dimensiones a partir de la teoría de Einstein de la relatividad general. Allí, la posición de un objeto se especifica por tres coordenadas en el espacio y una coordenada en el tiempo. Ya sabemos que conforme determina la relatividad especial, no existe un tiempo absoluto; el tiempo de cada uno es distinto del de los demás, dependiendo de la velocidad a la que se mueva y de quién sea el observador. La trayectoria de un objeto en el espacio-tiempo se denomina línea de universo. La relatividad general nos explica lo que es un espacio-tiempo curvo con las posiciones y movimientos de las partículas de materia.

La curvatura del espacio-tiempo es la propiedad en que las leyes familiares de la geometría no son aplicables en regiones donde los campos gravitatorios son intensos. La relatividad general de Einstein nos explica y demuestra que el espacio-tiempo está íntimamente relacionado con la distribución de materia en el universo, y nos dice que el espacio se curva en presencia de masas considerables como planetas, estrellas o galaxias (entre otros).

En un espacio de sólo dos dimensiones, como una lámina de goma plana, la geometría de Euclides se aplica de manera que la suma de los ángulos internos de un triángulo en la lámina es de 180°. Si colocamos un objeto masivo sobre la lámina de goma, la lámina se distorsionará al hundirse bajo la presión de la masa que soporta y los caminos de los objetos que se muevan sobre ella se curvarán. Esto es, en esencia, lo que ocurre con la relatividad general; donde está situada una estrella, el espacio está curvado y cualquier objeto que pase por allí será atraído hacia el centro de la estrella al caer, irremisiblemente, por las laderas del espacio curvado a su alrededor.

En los modelos cosmológicos más sencillos basados en los modelos de Friedman, la curvatura del espacio-tiempo está relacionada simplemente con la densidad media de la materia y se describe por una función matemática denominada métrica de Robertson-Walker.

Ya he explicado en otros trabajos relacionados con este asunto que el universo será lo que determine la materia en él contenida y, lógicamente, se podrá considerar plano, abierto o curvo y cerrado en función de su densidad crítica. El gráfico que se expone seguidamente nos da una idea de lo que sería en uno u otro caso:

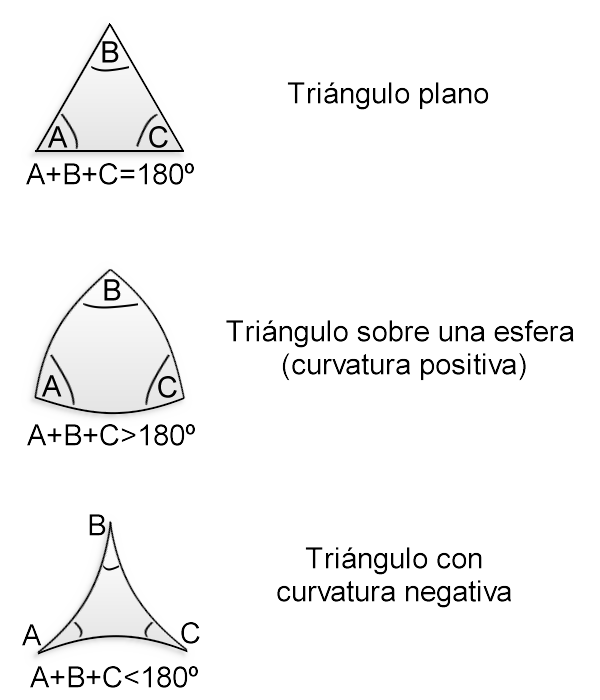
*Representación gráfica de los espacios que dan lugar a las tres posibles formas de universo antes referida, en función de la densidad crítica que hará un universo plano, un universo abierto o un universo curvo y cerrado.

Es posible que cualquier persona de mediana inteligencia, al encontrarse por vez primera ante estas cuestiones, quede fascinado por la manera tan simple y bella con que actúa la naturaleza, en la que todo, sin excepción, tiene una sencilla explicación. Son muchas las veces que, por falta de conocimientos necesarios, no podemos dar esa explicación sencilla que, estando ante nuestros ojos, por ignorancia, no podemos ver.

Hacer preguntas es fácil cuando se sabe lo que preguntar. Sin embargo, hay cuestiones sobre las que no podemos ni hacer una sencilla pregunta, toda vez porque la falta de conocimiento sobre dicho tema nos limita e impide preguntar sobre lo que desconocemos. Cuando adquirimos nuevos conocimientos hemos obtenido la llave para poder abrir una puerta que nos deja pasar hasta niveles superiores de conocimientos. Sin embargo, al entrar en dicho espacio, también nos encontramos con otras puertas que están cerradas y de las que no tenemos las llaves para poder abrirlas y contemplar su interior. Dichas puertas cerradas tienen un rótulo:

• Teoría de supercuerdas o su unificación en la teoría M.
• Bosón de Higgs.
• Teoría de la gravitación cuántica.
• Materia oscura.
• Ondas gravitacionales de agujeros negros.
• Agujeros de gusano y viajes en el tiempo.

Y otras muchas puertas cerradas con letreros de preguntas incontestables y que de manera incansable perseguimos.

[...]

Volver al índice